Ольга Петровна
ГБОУ ООШ пос. Журавли
м.р. Волжский Самарской области
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по геометрии
Содержание
- 1. Презентация к уроку по геометрии
- 2. Слайд 2
- 3. Ход урокаI.Организационный моментСообщить тему урока, сформулировать цели
- 4. СВАDFEДано: АBCD- прямоугольник, С –
- 5. Проверка домашнего заданияПроверить решение дополнительной задачи и
- 6. Задача № 455 Решение:Sпрям. =ab. Sпола=5,5 ∙
- 7. Работа по индивидуальным карточкам I уровень (карточка
- 8. АBCNМDРешение задач с целью подготовки учащихся к
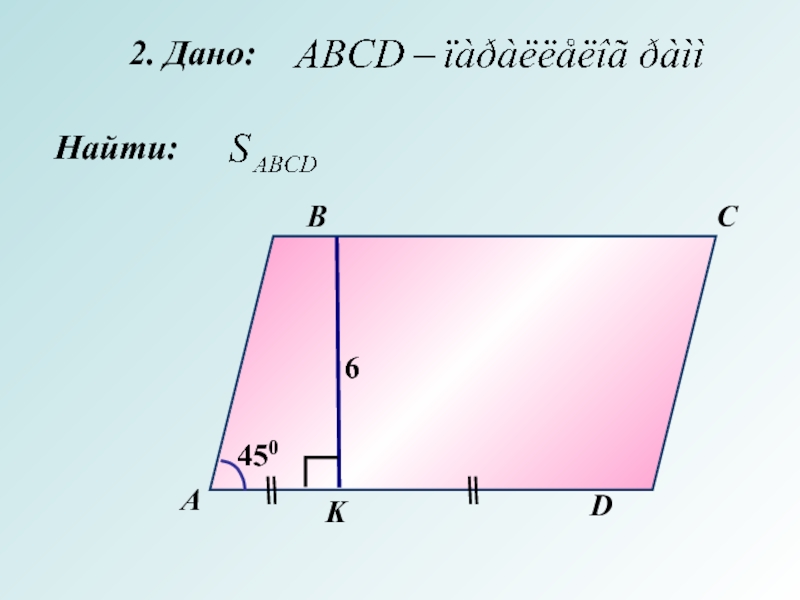
- 9. Найти:2. Дано:АBCDK6450
- 10. АBCDHIII.Изучение нового материала Высота параллелограммаВвести понятие
- 11. Теорема: Sпар-ма = а∙ha, где а – сторона параллелограмма, ha – высота, проведенная к ней.АВСDHEha
- 12. 14АВСDК8,1
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Благодарю за урок.Спасибо за внимание!
Цели урока:Вывести формулу для вычисления площади параллелограмма и показать применение этой формулы в процессе решения задач.Совершенствовать навыки решения задач.
Слайд 2 Цели урока:
Вывести
формулу для вычисления площади параллелограмма и показать применение этой формулы в процессе решения задач.
Совершенствовать навыки решения задач.
Совершенствовать навыки решения задач.
Слайд 3Ход урока
I.Организационный момент
Сообщить тему урока, сформулировать цели урока.
II.Актуализация знаний учащихся
1)К доске
вызываются два ученика для оформления решения домашней задачи.
2)Работа по индивидуальным карточкам.
3)Проведение теоретического опроса.
Теоретический опрос
Перечислите основные свойства площадей.
Сформулируйте и докажите теорему о площади прямоугольника
2)Работа по индивидуальным карточкам.
3)Проведение теоретического опроса.
Теоретический опрос
Перечислите основные свойства площадей.
Сформулируйте и докажите теорему о площади прямоугольника
Слайд 4С
В
А
D
F
E
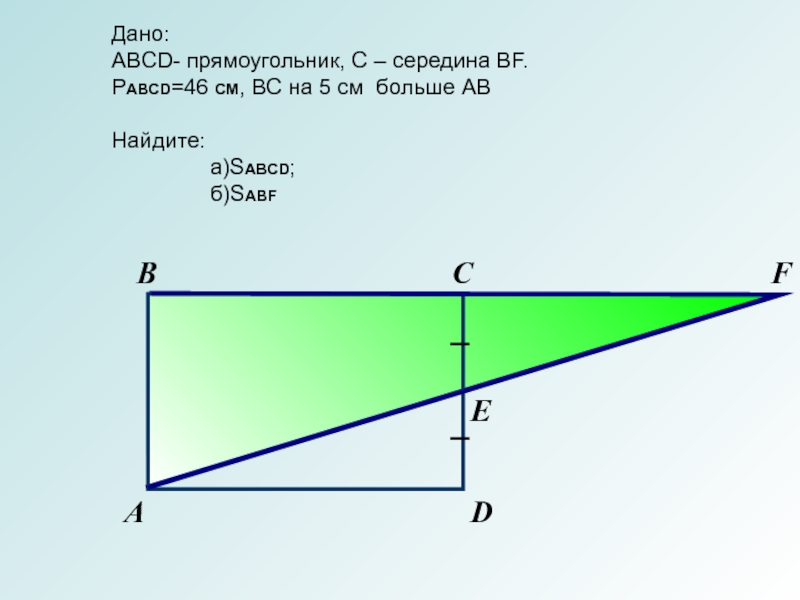
Дано:
АBCD- прямоугольник, С – середина BF.
PABCD=46 СМ, BC на 5 см больше AB
Найдите:
а)SABCD;
б)SABF
Слайд 5Проверка домашнего задания
Проверить решение дополнительной задачи и задачи №455.
Решение дополнительной задачи:
а)Так как PABCD=46 см, BC на 5 см больше AB, то PABCD=AB+BC+CD+DA=AB+(AB+5)+AB+(AB+5)=46 (учтено, что BC=AD=AB+5 см, AB=CD).
Тогда AB=9см, BC=14 см, SABCD=AB ∙ BC=9 ∙ 14=126см².
б)ΔADE=ΔFCE по катету и острому углу (CE=BC=AF, уголCEF=углу AED как вертикальные), тогда SADE=SFCT, и SABF=SABCE+SCEF=SABCE+SADE=SABCD=126 см².
Ответ: а)SABCD=126 см²; б) SABF=126 см².
Наводящие вопросы:
Как найти стороны прямоугольника, если известно, что его периметр
равен 46 см, а сторона ВС на 5 см больше АВ?
Какая формула применяется для вычисления площади прямоугольника?
Что вы можете сказать о площадях прямоугольника АВСD и треугольника ABF? Почему?
а)Так как PABCD=46 см, BC на 5 см больше AB, то PABCD=AB+BC+CD+DA=AB+(AB+5)+AB+(AB+5)=46 (учтено, что BC=AD=AB+5 см, AB=CD).
Тогда AB=9см, BC=14 см, SABCD=AB ∙ BC=9 ∙ 14=126см².
б)ΔADE=ΔFCE по катету и острому углу (CE=BC=AF, уголCEF=углу AED как вертикальные), тогда SADE=SFCT, и SABF=SABCE+SCEF=SABCE+SADE=SABCD=126 см².
Ответ: а)SABCD=126 см²; б) SABF=126 см².
Наводящие вопросы:
Как найти стороны прямоугольника, если известно, что его периметр
равен 46 см, а сторона ВС на 5 см больше АВ?
Какая формула применяется для вычисления площади прямоугольника?
Что вы можете сказать о площадях прямоугольника АВСD и треугольника ABF? Почему?
Слайд 6Задача № 455
Решение:
Sпрям. =ab. Sпола=5,5 ∙ 6=33 (м ²).
Sдощечки=5 ∙
30=150 (см ²)=0,015 (м ²).
Чтобы найти количество требуемых дощечек, нужно
Sпола разделить на Sдощечки:
33:0,015=2200 (дощечки).
Ответ: 2200
Наводящие вопросы:
-Как сосчитать, сколько дощечек паркета нужно для покрытия пола?
Что для этого нужно знать?
-Как найти площадь пола? А площадь одной дощечки?
-Как перевести квадратный сантиметр в квадратный метр?
Чтобы найти количество требуемых дощечек, нужно
Sпола разделить на Sдощечки:
33:0,015=2200 (дощечки).
Ответ: 2200
Наводящие вопросы:
-Как сосчитать, сколько дощечек паркета нужно для покрытия пола?
Что для этого нужно знать?
-Как найти площадь пола? А площадь одной дощечки?
-Как перевести квадратный сантиметр в квадратный метр?
Слайд 7Работа по индивидуальным карточкам
I уровень (карточка №1)
Периметр квадрата равен 20
см. Прямоугольник имеет
такую же площадь, что и квадрат, а одна из его сторон равна 10 см. найдите периметр прямоугольника.
2. Найдите площадь прямоугольника с периметром 60 см и отношением сторон 1:2.
II уровень (карточка №2)
1. Биссектриса угла А прямоугольника ABCD разбивает сторону ВС на отрезки, равные 4 и 5 см. Найдите площадь прямоугольника.
2. В прямоугольнике MNKP сторона MP равна 8 см, а расстояние от точки пересечения диагоналей до этой стороны равно 5 см. Чему равна площадь этого прямоугольника?
III уровень (карточка №3)
1. Высота BD треугольника ABC равна 8 см и делит сторону AC на отрезки, равные 5 и 6 см. Найдите площадь треугольника?
2. Диагонали ромба равны 10 и 12 см. Чему равна его площадь?
такую же площадь, что и квадрат, а одна из его сторон равна 10 см. найдите периметр прямоугольника.
2. Найдите площадь прямоугольника с периметром 60 см и отношением сторон 1:2.
II уровень (карточка №2)
1. Биссектриса угла А прямоугольника ABCD разбивает сторону ВС на отрезки, равные 4 и 5 см. Найдите площадь прямоугольника.
2. В прямоугольнике MNKP сторона MP равна 8 см, а расстояние от точки пересечения диагоналей до этой стороны равно 5 см. Чему равна площадь этого прямоугольника?
III уровень (карточка №3)
1. Высота BD треугольника ABC равна 8 см и делит сторону AC на отрезки, равные 5 и 6 см. Найдите площадь треугольника?
2. Диагонали ромба равны 10 и 12 см. Чему равна его площадь?
Слайд 8
А
B
C
N
М
D
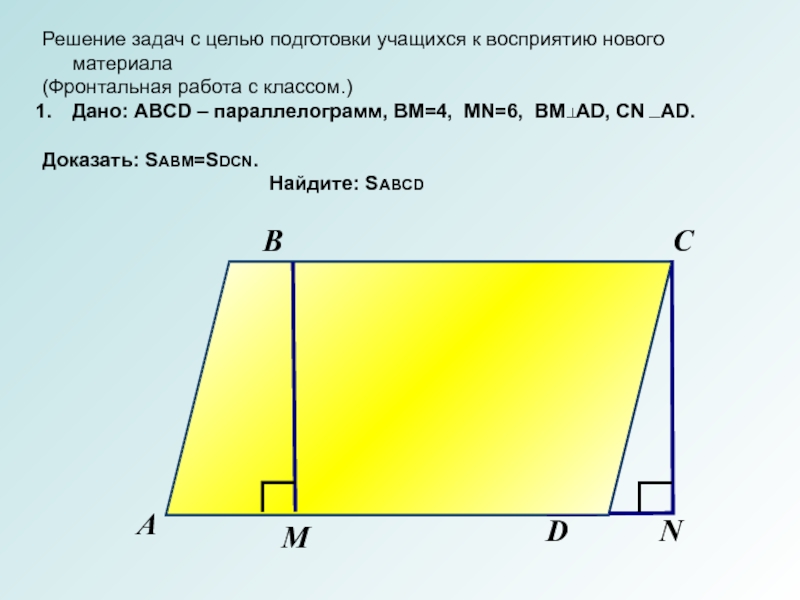
Решение задач с целью подготовки учащихся к восприятию нового материала
(Фронтальная работа
с классом.)
Дано: ABCD – параллелограмм, BM=4, MN=6, BM AD, CN AD.
Доказать: SABM=SDCN.
Найдите: SABCD
Дано: ABCD – параллелограмм, BM=4, MN=6, BM AD, CN AD.
Доказать: SABM=SDCN.
Найдите: SABCD
Слайд 10
А
B
C
D
H
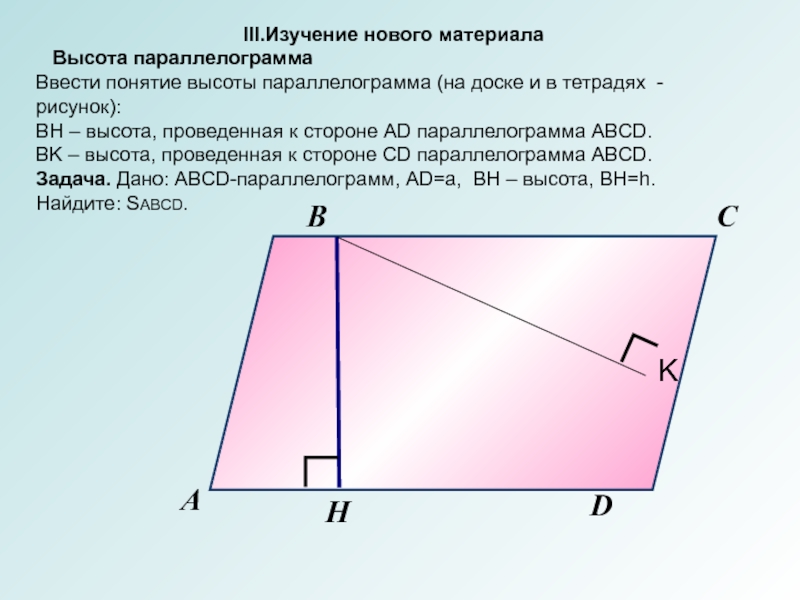
III.Изучение нового материала
Высота параллелограмма
Ввести понятие высоты параллелограмма (на
доске и в тетрадях - рисунок):
BH – высота, проведенная к стороне AD параллелограмма ABCD.
BK – высота, проведенная к стороне CD параллелограмма ABCD.
Задача. Дано: ABCD-параллелограмм, AD=а, BH – высота, BH=h.
Найдите: SABCD.
BH – высота, проведенная к стороне AD параллелограмма ABCD.
BK – высота, проведенная к стороне CD параллелограмма ABCD.
Задача. Дано: ABCD-параллелограмм, AD=а, BH – высота, BH=h.
Найдите: SABCD.
K
Слайд 11
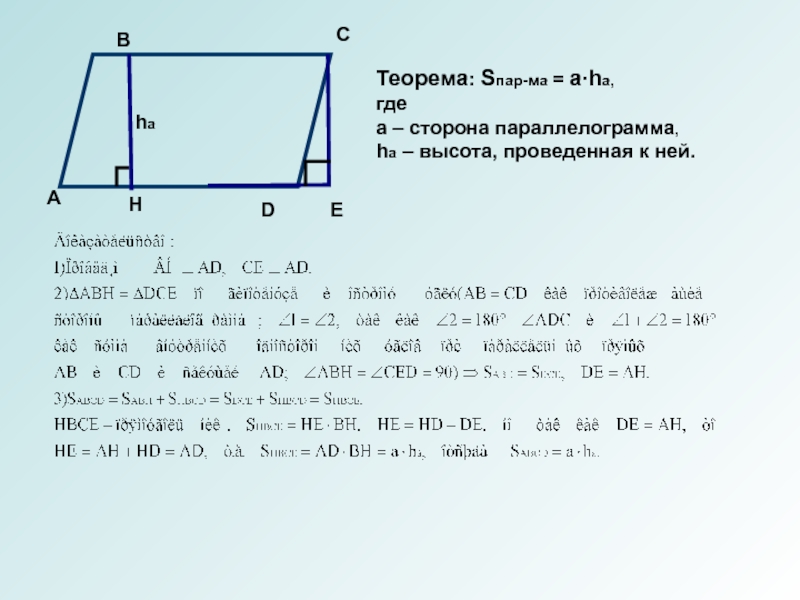
Теорема: Sпар-ма = а∙ha,
где
а – сторона параллелограмма,
ha –
высота, проведенная к ней.
А
В
С
D
H
E
ha