- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку на тему Площадь криволинейной трапеции и интеграл
Содержание
- 1. Презентация к уроку на тему Площадь криволинейной трапеции и интеграл
- 2. Что такое криволинейная трапеция?Как вычислить площадь криволинейной
- 3. Что такое криволинейная трапеция?y=f(x)Пусть на [a,b] оси
- 4. Слайд 4
- 5. Как вычислить площадь криволинейной трапеции?Теорема: Если f
- 6. Ньютон, ИсаакЛейбниц, Готфрид ВильгельмVS
- 7. Интегралот лат. integer — целый, то есть
- 8.
Что такое криволинейная трапеция?Как вычислить площадь криволинейной трапеции? Основная теорема.Другой подход к вычислению площади криволинейной трапеции. Интеграл.
Слайд 2Что такое криволинейная трапеция?
Как вычислить площадь криволинейной трапеции? Основная теорема.
Другой подход
к вычислению площади криволинейной трапеции. Интеграл.
Слайд 3Что такое криволинейная трапеция?
y=f(x)
Пусть на [a,b] оси Ox задана непрерывная функция
f(x), такая что f(x)≥0, xϵ[a,b] и f(x)>0, x ϵ(a,b).
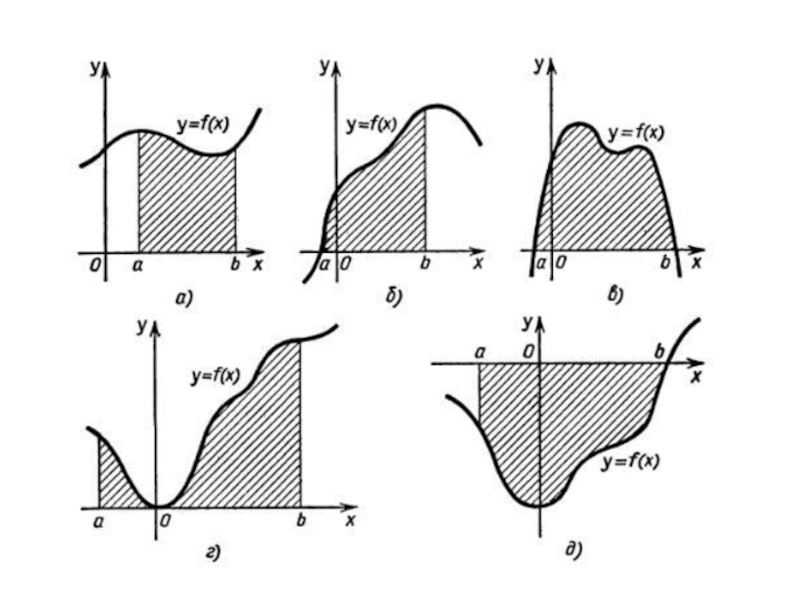
Фигуру, ограниченную графиком этой функции, отрезком [a,b] и прямыми x=a, x=b, называют криволинейной трапецией.
Фигуру, ограниченную графиком этой функции, отрезком [a,b] и прямыми x=a, x=b, называют криволинейной трапецией.
![Что такое криволинейная трапеция?y=f(x)Пусть на [a,b] оси Ox задана непрерывная функция f(x), такая что f(x)≥0, xϵ[a,b] и](/img/thumbs/4f94382bfe4822b4c385ba69c90436b1-800x.jpg "Презентация к уроку на тему Площадь криволинейной трапеции и интеграл Что такое криволинейная трапеция?y=f(x)Пусть на [a,b] оси Ox задана непрерывная функция")
Слайд 5Как вычислить площадь криволинейной трапеции?
Теорема: Если f непрерывная и неотрицательная на
[a,b] функция, а F её первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a,b]
S=F(b)-F(a),
где F(x) – любая первообразная f(x).
S=F(b)-F(a),
где F(x) – любая первообразная f(x).
![Как вычислить площадь криволинейной трапеции?Теорема: Если f непрерывная и неотрицательная на [a,b] функция, а F её первообразная](/img/thumbs/85f017376d6fda81d0a848fa82f0689d-800x.jpg "Презентация к уроку на тему Площадь криволинейной трапеции и интеграл Как вычислить площадь криволинейной трапеции?Теорема: Если f непрерывная и неотрицательная на")
Слайд 7Интеграл
от лат. integer — целый, то есть целая, вся — площадь
(был предложен в 1696 г. Иоганном Бернулли)
Символ (∫) образовался из буквы S (от лат. summa — сумма)
Символ (∫) образовался из буквы S (от лат. summa — сумма)
