Кирина Ольга Владимировна, учитель математики
2013-2014уч.г
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики Повторяем комбинаторику
Содержание
- 1. Презентация к уроку математики Повторяем комбинаторику
- 2. Не нужно нам владеть клинком, Не
- 3. Основная цель:• изучить теоретический материал по выбранной
- 4. Комбинаторика•(Комбинаторный анализ) — раздел математики, изучающий дискретные
- 5. Методы КомбинаторикиПерестановкой из n элементов (например чисел
- 6. Пример задачи •При игре в кости бросаются
- 7. Способы решения комбинаторных задач:Таблица вариантовДерево вариантовПравило умноженияКомбинаторику
- 8. Таблица вариантовСколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9?02412459101214202224404244505254909294Ответ:15 чисел.
- 9. Дерево вариантовИз чисел 1, 5, 9 составить
- 10. На завтрак можно выбрать булочку, кекс, пряники
- 11. Слайд 11
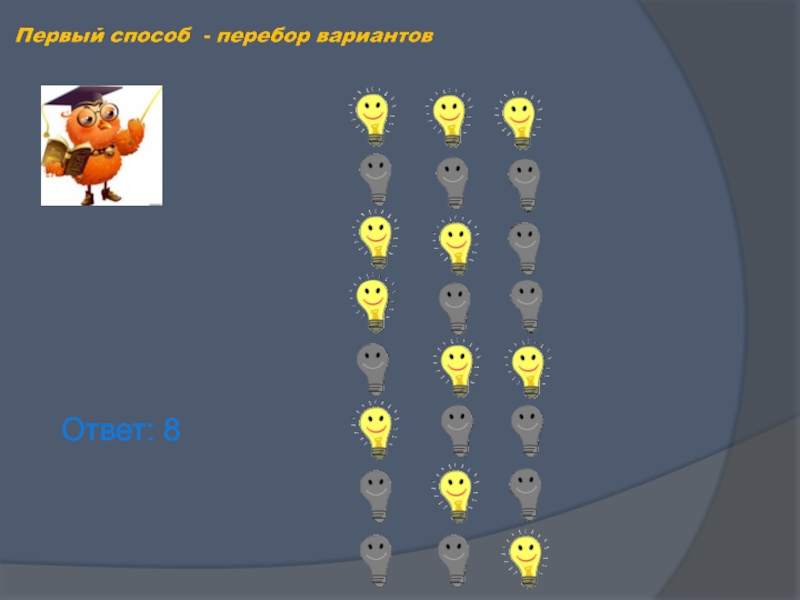
- 12. Ответ: 8
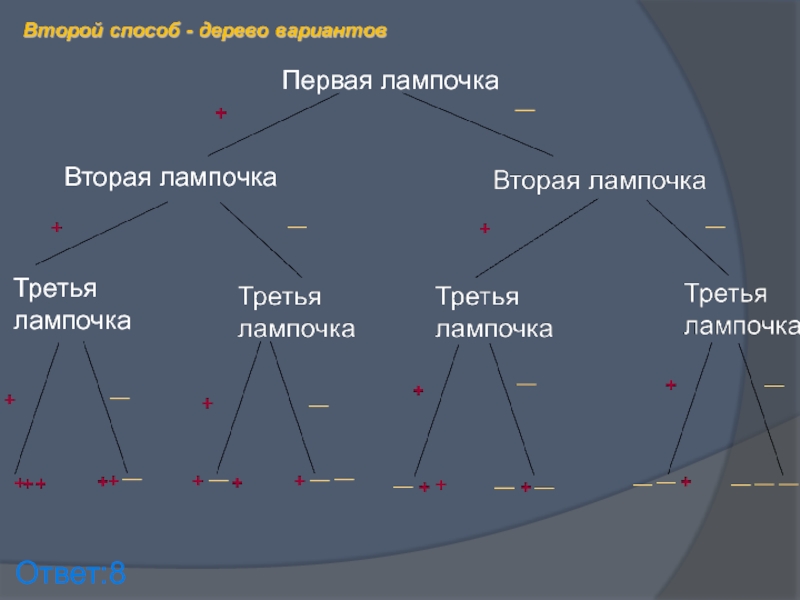
- 13. Первая лампочкаВторая лампочкаТретья лампочка—Ответ:8—
- 14. Для каждой лампочки возможны два исхода (гореть
- 15. Всего вариантов расписанияРасставляем предметы по порядку654312ГеометрияРусский языкЛитератураБиологияФизкультураАнглийский язык1*2*3*4*5*6*=720
- 16. Дяде Федору для приема гостей мама и
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. №1№2№3№4№5№6621543
- 25. 6*5*4*3*2*1=720 дней- почти 2 года
- 26. ПерестановкиПерестановкой из n элементов называется каждое расположение этих элементов в определенном порядке.
- 27. Пример №1.Сколькими способами можно расставить 8 участниц
- 28. Пример №2.Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0,2,4,6?
- 29. Решите задачуСколькими способами могут сесть в автомобиль 5 человек, каждый из которых может быть водителем?
- 30. Сколькими способами 4 человека могут разместиться на четырехместной скамейке?
- 31. I. Вычислите:3!5!3!=1*2*3=65!=1*2*3*4*5=120II. Сколько перестановок можно получить из букв, составляющих слово «апельсин».
- 32. Размещение
- 33. ПримерУчащиеся 2 класса изучают 9 предметов. Сколькими
- 34. Решите задачи:Сколькими способами может разместиться семья из
- 35. На станции 7 запасных путей. Сколькими способами можно расставить на них 4 поезда?
- 36. СочетаниеСочетанием из n элементов по k называется
- 37. ПримерИз набор, состоящего из 15 красок, надо
- 38. Решите задачи:1)В классе 7 человек успешно занимаются
- 39. 3)Учащимся дали список из 10 книг, которые
- 40. Литература1.Алгебра. Элементы статистики и теории вероятностей. Учебное
Не нужно нам владеть клинком, Не ищем славы громкой. Тот побеждает, кто знаком С искусством мыслить тонким Уордсворд
Слайд 1 презентация к уроку математики 9 класс « повторяем комбинаторику» подготовка к ГИА по
математике
модуль «Реальная математика»
Слайд 2Не нужно нам владеть клинком, Не ищем славы громкой. Тот побеждает,
кто знаком
С искусством мыслить тонким
Уордсворд
Слайд 3Основная цель:
• изучить теоретический
материал по выбранной теме;
•научиться решать комбинаторные задачи;
развить
логическое и творческое мышление;
подготовиться к ГИА по математике.
подготовиться к ГИА по математике.
Слайд 4Комбинаторика
•(Комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки,
размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения в различных областях знаний (например в генетике, информатике, статистической физике).
•Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
•Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Слайд 5Методы Комбинаторики
Перестановкой из n элементов (например чисел 1,2,…,n) называется всякий упорядоченный
набор из этих элементов. Перестановка также является размещением из n элементов по n.
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.
Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.
Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.
Слайд 6Пример задачи
•При игре в кости бросаются две кости, и выпавшие
очки складываются; сколько существует комбинаций, таких, что сумма очков на верхних гранях равна двенадцати?
Решение: Каждый возможный исход соответствует функции (аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 даёт нам нужный результат 12. Таким образом существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, такая, что сумма очков на верхних гранях равна двенадцати.
Слайд 7Способы решения комбинаторных задач:
Таблица вариантов
Дерево вариантов
Правило умножения
Комбинаторику можно рассматривать как часть
теории множеств – любую комбинаторную задачу можно свести к задаче о конечных множествах и их отображениях.
Слайд 8Таблица вариантов
Сколько четных двузначных чисел можно составить из цифр 0,1,2,4,5,9?
0
2
4
1
2
4
5
9
10
12
14
20
22
24
40
42
44
50
52
54
90
92
94
Ответ:15 чисел.
Слайд 9Дерево вариантов
Из чисел 1, 5, 9 составить трёхзначное число без повторяющихся
цифр.
1
5
9
159
195
519
591
915
951
2 комбинации
2 комбинации
2 комбинации
Всего 2•3=6 комбинаций.
Слайд 10На завтрак можно выбрать булочку, кекс, пряники или печенье, запить можно
чаем, соком или кефиром. Сколько вариантов завтрака есть?
напитки
х/б
изд.
чай
сок
кефир
булочка
кекс
пряники
печенье
булочка
Испытание А имеет 3 варианта (исхода), а испытание В-4, всего вариантов
независимых испытаний А и В 3•4=12.
чай
кекс
сок
кефир
пече-
нье
пряники
Слайд 14Для каждой лампочки возможны два исхода (гореть или не гореть), а
лампочек три, значит
2*2*2=8
Слайд 15Всего вариантов расписания
Расставляем предметы по порядку
6
5
4
3
1
2
Геометрия
Русский язык
Литература
Биология
Физкультура
Английский язык
1*2*3*4*5*6*=720
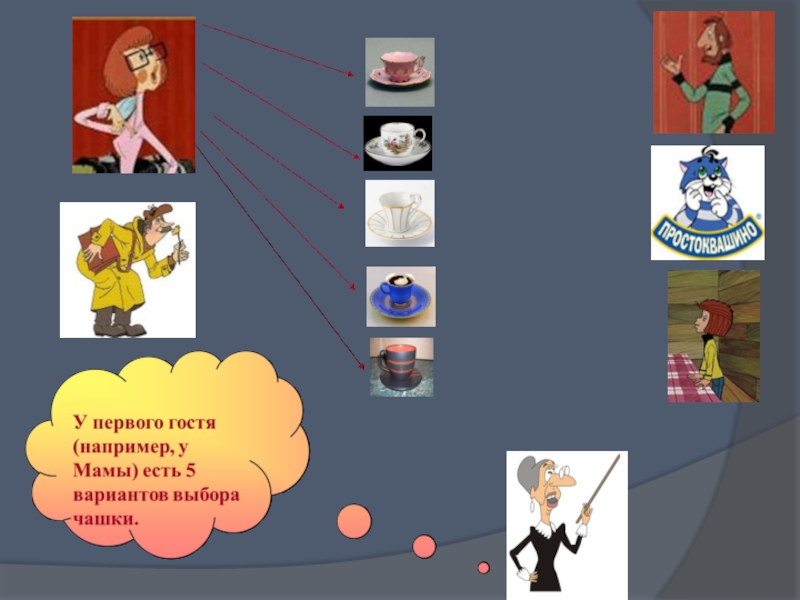
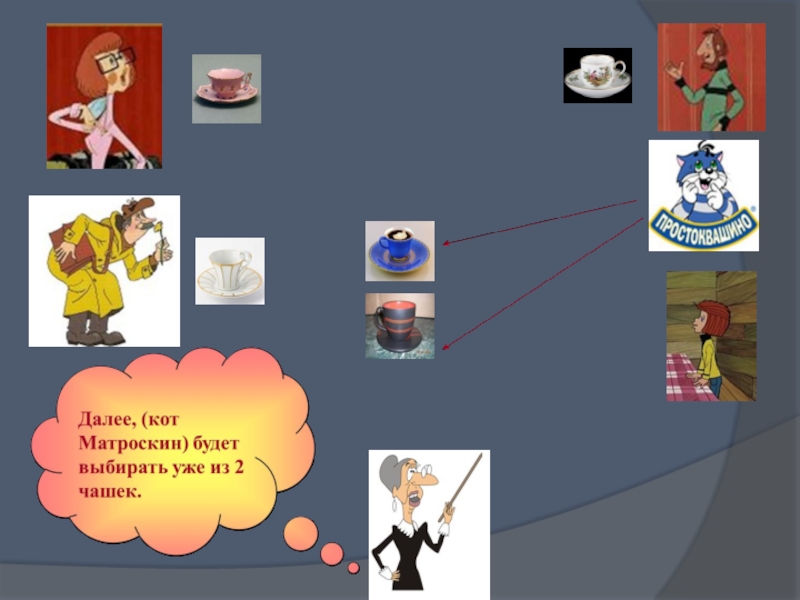
Слайд 16Дяде Федору для приема гостей мама и папа подарили 5 разных
чашек. Сколькими способами можно разделить чашки между гостями?
В гости к Дяде Федору пришли папа, мама, кот Матроскин и почтальон Печкин.
В гости к Дяде Федору пришли папа, мама, кот Матроскин и почтальон Печкин.
Слайд 26Перестановки
Перестановкой из n элементов называется каждое расположение этих элементов в определенном
порядке.
Слайд 27Пример №1.
Сколькими способами можно расставить 8 участниц финального забега на восьми
беговых дорожках?
Значит, существует 40 320 способов расстановки участниц забега на восьми беговых дорожках.
Слайд 28Пример №2.
Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно
составить из цифр 0,2,4,6?
Слайд 29Решите задачу
Сколькими способами могут сесть в автомобиль 5 человек, каждый из
которых может быть водителем?
Слайд 31I. Вычислите:
3!
5!
3!=1*2*3=6
5!=1*2*3*4*5=120
II. Сколько перестановок можно получить из букв, составляющих слово «апельсин».
Слайд 33Пример
Учащиеся 2 класса изучают 9 предметов. Сколькими способами можно составить расписание
на один день, чтобы в нем было 4 различных предмета?
Итак, мы нашли, что расписание можно составить 3024 способами.
Слайд 34Решите задачи:
Сколькими способами может разместиться семья из трех человек в четырехместном
купе, если других пассажиров в купе нет?
Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно сделать?
Слайд 36Сочетание
Сочетанием из n элементов по k называется любое множество, составленное из
k элементов, выбранных из данных n элементов.
Слайд 37Пример
Из набор, состоящего из 15 красок, надо выбрать 3 краски для
окрашивания шкатулки. Сколькими способами можно сделать этот выбор?
Слайд 38Решите задачи:
1)В классе 7 человек успешно занимаются математикой. Сколькими способами можно
выбрать из них двоих для участия в математической олимпиаде?
2)В магазине «Филателия» продается 8 различных наборов марок, посвящённых спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Слайд 393)Учащимся дали список из 10 книг, которые рекомендуется прочитать во время
каникул. Сколькими способами ученик может выбрать из них 6 книг?
4)На плоскости отмечено 8 точек, никакие три из которых не лежат на одной прямой. Сколько прямых можно провести через эти точки?
Слайд 40Литература
1.Алгебра. Элементы статистики и теории вероятностей. Учебное пособие для учащихся 7-9
классов общеобразовательных учреждений. Макарычев Ю. Н., Миндюк Н. Г. Под ред. С. А. Теляковского Москва Просвещение 2003г.
2. http://sernam.ru/book_e_math.php?id=55
3. http://ru.wikipedia.org/wiki/%D0%E0%E7%EC%E5%F9%E5%ED%E8%E5
4. http://ru.wikipedia.org/wiki/%D0%A1%D0%BE%D1%87%D0%B5%D1%82%D0%B0%D0%BD%D0%B8%D1%8F
2. http://sernam.ru/book_e_math.php?id=55
3. http://ru.wikipedia.org/wiki/%D0%E0%E7%EC%E5%F9%E5%ED%E8%E5
4. http://ru.wikipedia.org/wiki/%D0%A1%D0%BE%D1%87%D0%B5%D1%82%D0%B0%D0%BD%D0%B8%D1%8F
