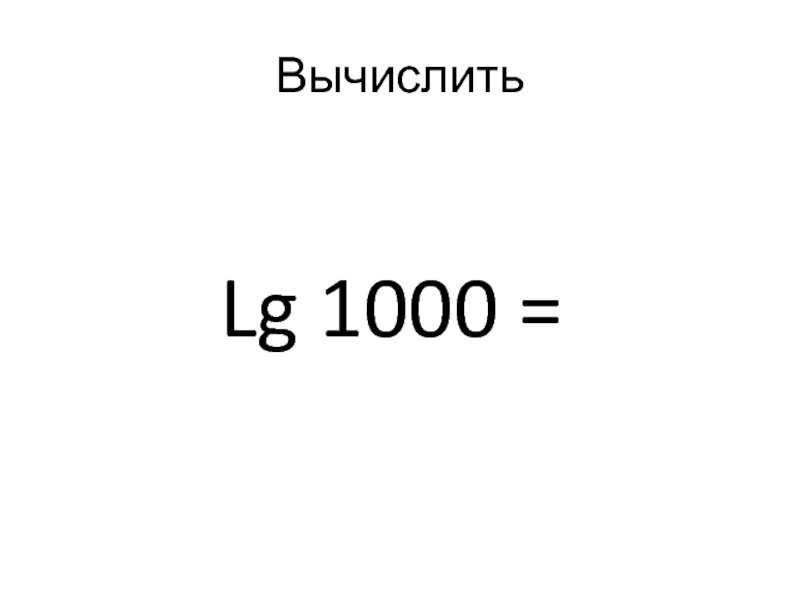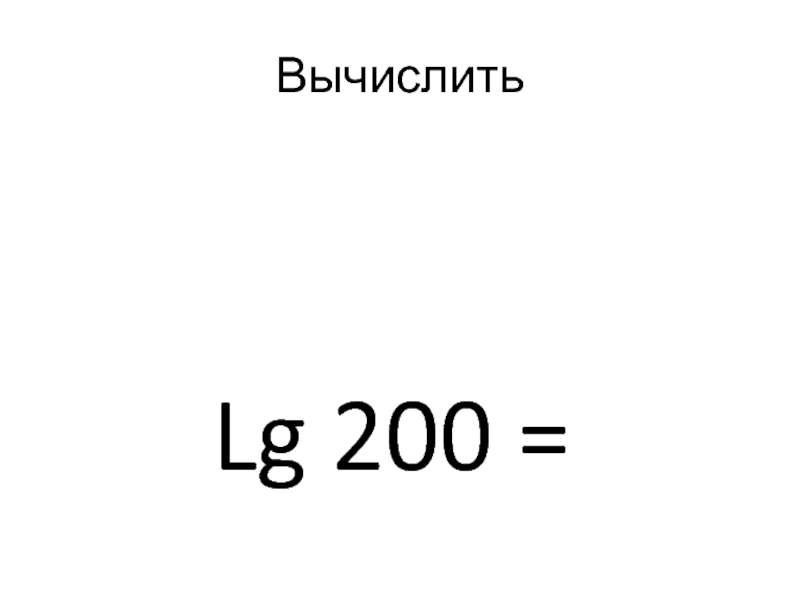- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики на тему: Логарифм с произвольным основанием
Содержание
- 1. Презентация к уроку математики на тему: Логарифм с произвольным основанием
- 2. Слайд 2
- 3. Решить уравнение2х = 8
- 4. 23 = 8Ответ: х = 3
- 5. Компоненты равенства2 – основание степени8 – степеньx
- 6. Эту задача - нахождение логарифма.Логарифмом числа
- 7. Слайд 7
- 8. Вычислите и запишите с помощью
- 9. Ответ
- 10. Вычислите и запишите с помощью логарифмов равенство73=
- 11. Ответ 73 =343
- 12. Решение примеровСледующее равенство запишите в виде показательного равенства.Log3 27 = 3
- 13. Ответ 33 = 27
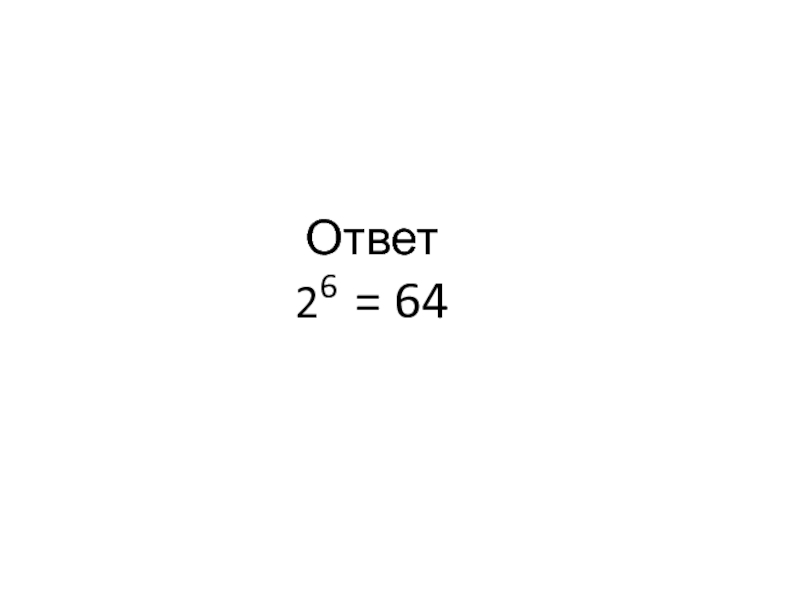
- 14. Запишите в виде показательного равенства
- 15. Ответ 26 = 64
- 16. Реши самостоятельно Найдите число, если его
- 17. Правильные ответыLog 3 9=2Log5625=4Log381=4
- 18. Десятичные логарифмы Наиболее употребительными являются системы
- 19. Вычислить
- 20. ОтветLg 100 = 2 → 102 = 100
- 21. Вычислить Lg 1000 =
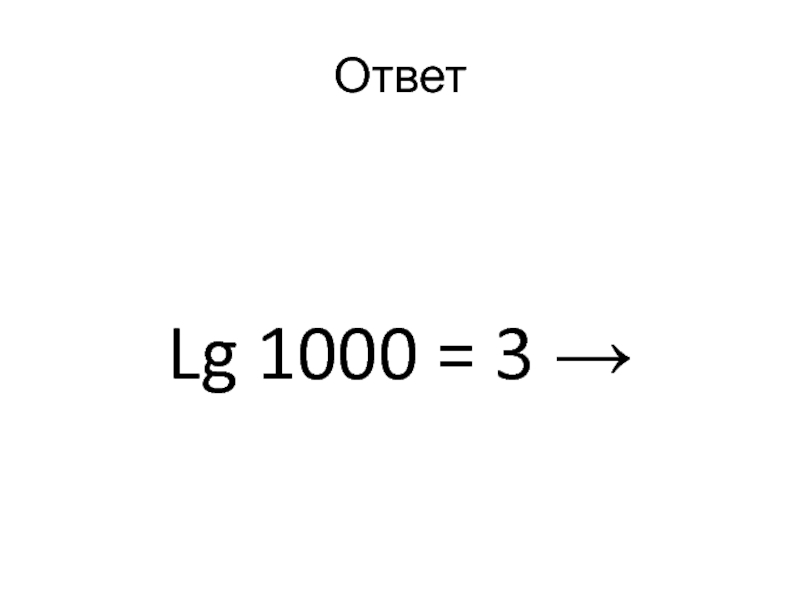
- 22. ОтветLg 1000 = 3 →
- 23. Вычислить Lg 200 =
- 24. Логарифм числа не равного целой степени числа
- 25. Логарифм числа Характеристика логарифма всякого числа
- 26. ВычислитьLg 200= 2,30102-характеристика0,3010- мантиса
- 27. ВычислитьLg 5234
- 28. ОтветLg 5234=3,7188
- 29. Вычислить Lg 0,002=
- 30. Ответ Характеристика логарифма правильной десятичной
- 31. ВычислитьLg 0,02=
- 32. Ответ Lg 0,02=-2 + 0,3010=-1,699
- 33. Теоремы о
- 34. Логарифм частного равен логарифму делимого минус логарифм
- 35. Логарифм степени равен произведению показателя степени на
- 36. Решить уравнениеLg X = 4· Lg 2+Lg 3
- 37. Решение Lg X=Lg 24+Lg 3,
- 38. Вычислить N =
- 39. РешениеПрологарифмируем равенство по основанию 10.LgN = Lg
- 40. Решите уравнение15x=238
- 41. Логарифмируем равенство по основанию 10Lg15x = Lg238Применяем
- 42. Слайд 42
Решить уравнение2х = 8
Слайд 5Компоненты равенства
2 – основание степени
8 – степень
x = показатель степени
Задача. По
известному основанию и степени найти показатель степени.
Слайд 6Эту задача - нахождение логарифма.
Логарифмом числа b по основанию а
(а > 0 и а = 1) называется показатель степени, в которую надо возвести число а , чтобы получить число b.
Слайд 16Реши самостоятельно
Найдите число, если его логарифм равен 2
при основании 3 .
Найдите логарифм числа 625 по основанию 5
При каком основании логарифм 81 равен 4 ?
Найдите логарифм числа 625 по основанию 5
При каком основании логарифм 81 равен 4 ?
Слайд 18Десятичные логарифмы
Наиболее употребительными являются системы десятичных логарифмов.
У
них основание число 10.
Обозначение: Lg b = х → 10х = b.
Натуральными называются логарифмы, основание которых иррациональное число, обозначаемое буквой е.
Обозначение: Ln b = x → eх = b.
e = 2.71828…
Обозначение: Lg b = х → 10х = b.
Натуральными называются логарифмы, основание которых иррациональное число, обозначаемое буквой е.
Обозначение: Ln b = x → eх = b.
e = 2.71828…
Слайд 24Логарифм числа не равного целой степени числа 10
Если число не является
степенью числа 10 с натуральным показателем , то логарифм –
число иррациональное.
Целая часть приближенного значения логарифма называется его характеристикой
а дробная- мантисой.
число иррациональное.
Целая часть приближенного значения логарифма называется его характеристикой
а дробная- мантисой.
Слайд 25Логарифм числа
Характеристика логарифма всякого числа , большего единицы ,
на единицу меньше числа цифр , стоящих до запятой.
Слайд 30Ответ
Характеристика логарифма правильной десятичной дроби содержит столько отрицательных
единиц , сколько нулей слева до первой значащей цифры , считая нуль до запятой
Lg 0,002=-3+0,3010=-2,6990
Lg 0,002=-3+0,3010=-2,6990
Слайд 33
Теоремы о логарифмировании
Теорема 1
Логарифм произведения равен
сумме логарифмов сомножителей.
Loga (N1· N2) = LogaN1+LogaN2
Loga (N1· N2) = LogaN1+LogaN2
Слайд 34
Логарифм частного равен логарифму делимого минус логарифм делителя
Loga (N1 :
N2)=LogaN1 - LogaN2
Слайд 35
Логарифм степени равен произведению показателя степени на логарифм числа возвышаемого в
степень
LogaNk=k · LogaN
LogaNk=k · LogaN
Слайд 39Решение
Прологарифмируем равенство по основанию 10.
LgN = Lg 1001/100
LgN = 1/100 ·
Lg100
LgN = 1/100 · 2
LgN = 0.02
Число N находим по таблице антилогарифмов (стр68)
LgN = 1/100 · 2
LgN = 0.02
Число N находим по таблице антилогарифмов (стр68)
Слайд 41Логарифмируем равенство по основанию 10
Lg15x = Lg238
Применяем теоремы о логарифмах
X · Lg15 = Lg238
X = Lg238 : Lg15
X = 2.3766 : 1.1761
X = 2.02
X = Lg238 : Lg15
X = 2.3766 : 1.1761
X = 2.02