- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии Теорема Пифагора
Содержание
- 1. Презентация к уроку геометрии Теорема Пифагора
- 2. содержание Историческая справка Формулировка теоремы Пифагора Доказательство теоремы Еще несколько доказательств Реши задачи Решение задач Заключение
- 3. Историческая справкаСуществует замечательное соотношение между гипотенузой и
- 4. Формулировка теоремыАСВВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
- 5. Доказательство теоремы1. Достроим АВС до квадрата СКРД
- 6. Еще несколько доказательств теоремы ПифагораТеорема Пифагора (
- 7. Приведем одно из многочисленных геометрических доказательств теоремы
- 8. Этот рисунок демонстрирует старинное индийское доказательство теоремы
- 9. реши задачи 1.Дан прямоугольный треугольник KMN. KN
- 10. решение задач Задача 1Т. К. треугольник прямоугольный,
- 11. решение задач Задача 2Рассмотрим треугольник DFR –
- 12. решение задач Задача 3Дано : АВС –
- 13. заключение
Слайд 2содержание
Историческая справка
Формулировка теоремы Пифагора
Доказательство теоремы
Еще несколько
Реши задачи
Решение задач
Заключение
Слайд 3Историческая справка
Существует замечательное соотношение между гипотенузой и катетами прямоугольного треугольника, справедливость
Но изучение вавилонских клинописных таблиц и древних китайских рукописей показало, что это утверждение было известно задолго до Пифагора.
Заслуга же Пифагора состояла в том, что он открыл доказательство этой теоремы.
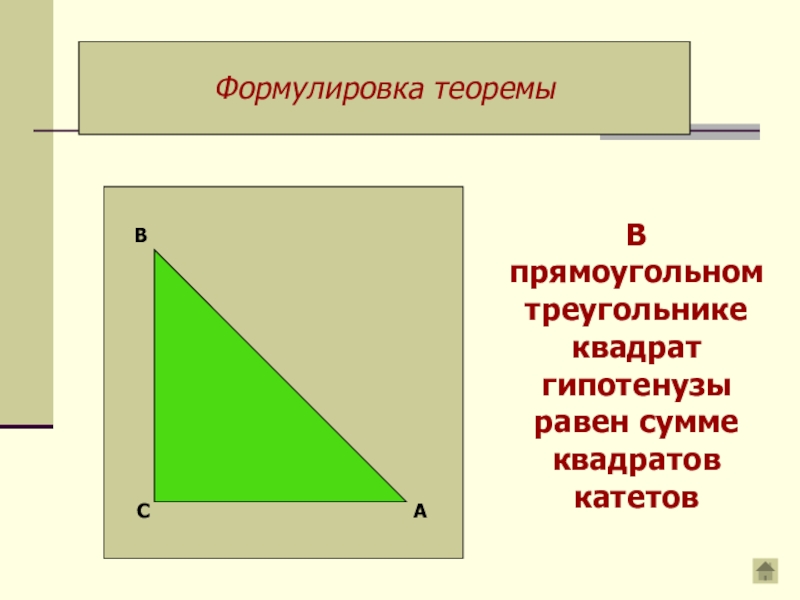
Слайд 4Формулировка теоремы
А
С
В
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 5Доказательство теоремы
1. Достроим
АВС до квадрата СКРД со стороной (
SСКРД= ( а + в)2 = а2 + 2ав + в2
2.
ВСА =
АКЕ =
ЕРМ =
МДВ ( по двум катетам )
С
А
В
Д
М
Р
Е
К
SВСА = SАКЕ = SЕРМ= SМДВ = ав/2
3. ВАЕМ – квадрат, SВАЕМ = c2
4. SСКРД= SВАЕМ+ SВСА+ SАКЕ+ SЕРМ+ SМДВ
5. ( а + в)2 = с2 + 4 * ав/2
а2 + 2ав + в2 = с2 + 2ав, откуда
с2 = а2 + в2
Дано:
АВС, Доказать: с2 = а2 + в2 Доказательство:
Слайд 6Еще несколько доказательств теоремы Пифагора
Теорема Пифагора ( другая формулировка)
Сумма площадей квадратов,
Именно так выглядела классическая формулировка теоремы. Картинка, иллюстрирующая теорему Пифагора, была ранее своеобразным символом геометрии, а в среде российских гимназистов получила название « Пифагоровы штаны».Саму теорему они переиначили так: «Пифагоровы штаны на все стороны равны». И в этой шуточной формулировке запоминали ее на всю жизнь.
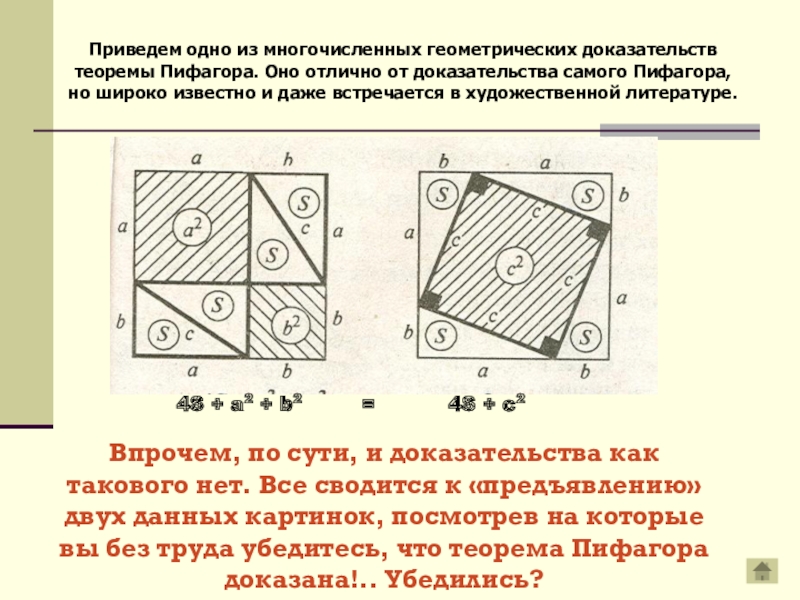
Слайд 7Приведем одно из многочисленных геометрических доказательств теоремы Пифагора. Оно отлично от
Впрочем, по сути, и доказательства как такового нет. Все сводится к «предъявлению» двух данных картинок, посмотрев на которые вы без труда убедитесь, что теорема Пифагора доказана!.. Убедились?
4S + a2 + b2 = 4S + c2
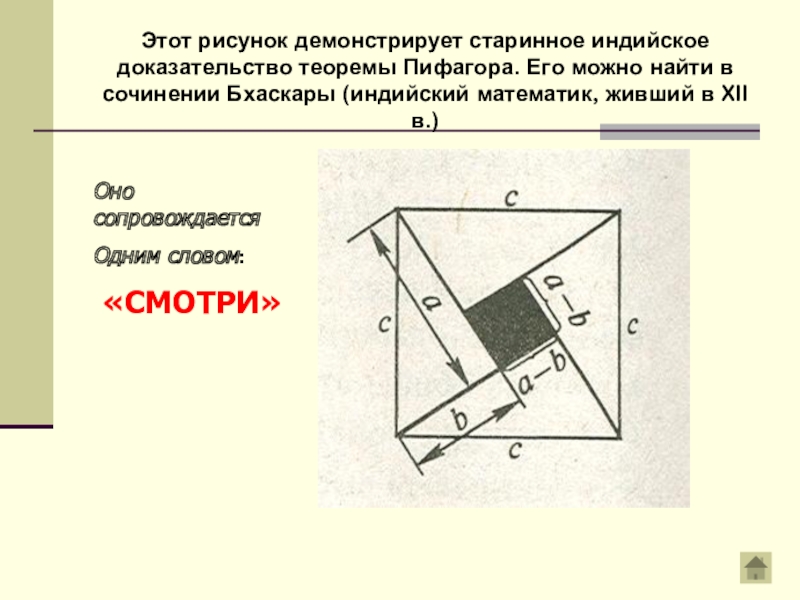
Слайд 8Этот рисунок демонстрирует старинное индийское доказательство теоремы Пифагора. Его можно найти
Оно сопровождается
Одним словом:
«СМОТРИ»
Слайд 9реши задачи
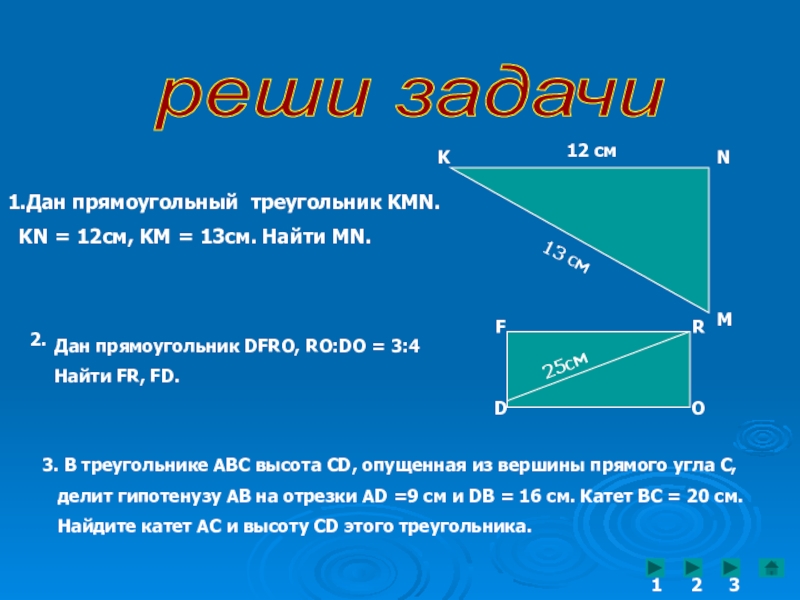
1.Дан прямоугольный треугольник KMN.
KN = 12cм, KM =
K
N
M
12 cм
13 см
2.
Дан прямоугольник DFRO, RO:DO = 3:4
Найти FR, FD.
F
R
O
D
25см
3. В треугольнике АВС высота CD, опущенная из вершины прямого угла С,
делит гипотенузу АВ на отрезки АD =9 см и DB = 16 см. Катет ВС = 20 см.
Найдите катет АС и высоту CD этого треугольника.
3
2
1
Слайд 10решение задач
Задача 1
Т. К. треугольник прямоугольный, то применим теорему Пифагора:
КМ2= KN2 + NM2 => MN2=KM2 – KN2 => MN2 = 169 -144 = 25, MN = 5см
Ответ : MN = 5 см.
решение задач
Слайд 11решение задач
Задача 2
Рассмотрим треугольник DFR – прямоугольный ( DFRO- прямоугольник
2. RO = FD и DO = FR (по свойству параллелограмма)
3. FD = 3x см и FR = 4x см, т.к. RO : DO = 3:4 и х – 1 часть
4. Используя теорему Пифагора, составим равенство : FD2+ FR2= DR2
5. 9х2 + 16х2 = 625 ( решаем уравнение)
25х2 = 625
х2 = 25
х1 = 5 , х2= - 5 ( - 5 не является решением задачи)
6. FD = 3 * 5 = 15(cm) FR = 4 * 5 = 20 (cm)
Ответ : FR = 20 см и FD = 15 см
решение задач
Слайд 12решение задач
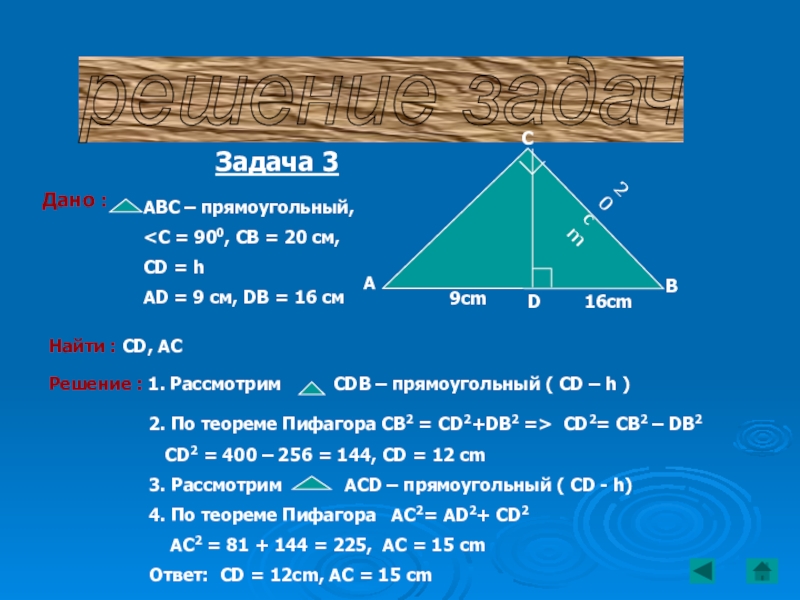
Задача 3
Дано :
АВС – прямоугольный,
CD = h
AD = 9 cм, DB = 16 см
Найти : CD, AC
B
C
A
D
20 cm
9cm
16cm
Решение : 1. Рассмотрим CDB – прямоугольный ( CD – h )
2. По теореме Пифагора CB2 = CD2+DB2 => CD2= CB2 – DB2
CD2 = 400 – 256 = 144, CD = 12 cm
3. Рассмотрим ACD – прямоугольный ( CD - h)
4. По теореме Пифагора AC2= AD2+ CD2
AC2 = 81 + 144 = 225, AC = 15 cm
Ответ: CD = 12cm, AC = 15 cm