- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии по теме: Некоторые свойства прямоугольных треугольников. Решение задач
Содержание
- 1. Презентация к уроку геометрии по теме: Некоторые свойства прямоугольных треугольников. Решение задач
- 2. Пусть математика сложна, Ее до края не познать,Откроет двери всем она,В них только надо постучать.
- 3. 1. Что такое треугольник?2. Что такое прямоугольный
- 4. 4. Сформулируйте первое свойство прямоугольных треугольниковСвойство 1:
- 5. 5. Сформулируйте второе свойство прямоугольных треугольниковСвойство 2:
- 6. 6. Сформулируйте третье свойство прямоугольных треугольниковСвойство 3:
- 7. № 1. Найдите острые углы прямоугольного треугольника,
- 8. № 1. Найдите острые углы прямоугольного треугольника,
- 9. № 2. Найдите острые углы прямоугольного треугольника,
- 10. № 2. Найдите острые углы прямоугольного треугольника,
- 11. № 259(учебник Геометрия 7-9 Атанасян Л.С., стр.81)
- 12. № 259(учебник Геометрия 7-9 Атанасян Л.С., стр.81)
- 13. Домашнее задание:Пункт 34 стр. 76-77 повторить,№ 256Творческое
- 14. Спасибо за урок
Слайд 2Пусть математика сложна,
Ее до края не познать,
Откроет двери всем она,
В
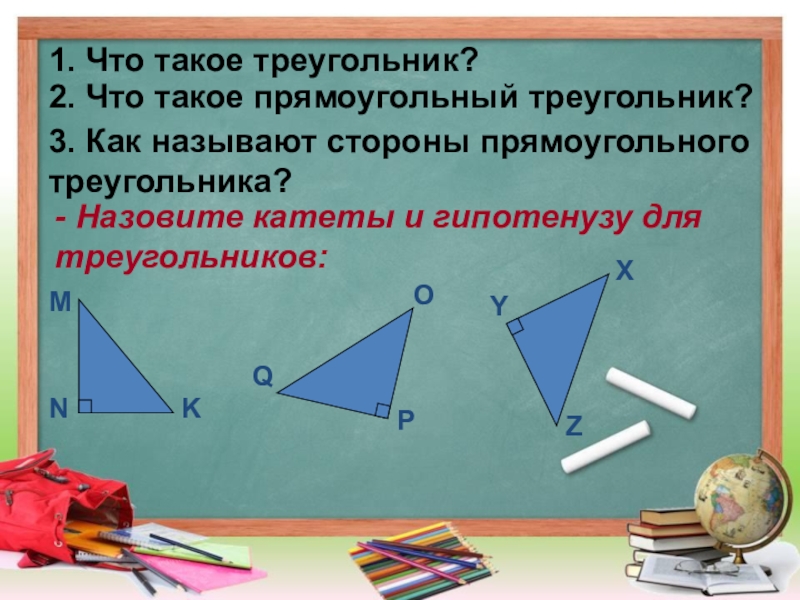
Слайд 31. Что такое треугольник?
2. Что такое прямоугольный треугольник?
3. Как называют стороны
треугольника?
- Назовите катеты и гипотенузу для
треугольников:
M
N
K
O
P
Q
X
Y
Z
Слайд 44. Сформулируйте первое свойство
прямоугольных треугольников
Свойство 1: Сумма двух острых углов
прямоугольного треугольника равна 90 °
- Найдите неизвестные элементы
A
B
C
∠A + ∠B =?
M
P
K
∠M = 35°
∠K = ?
∠K = 90° - 35° = 55°
∠A + ∠B = 90°
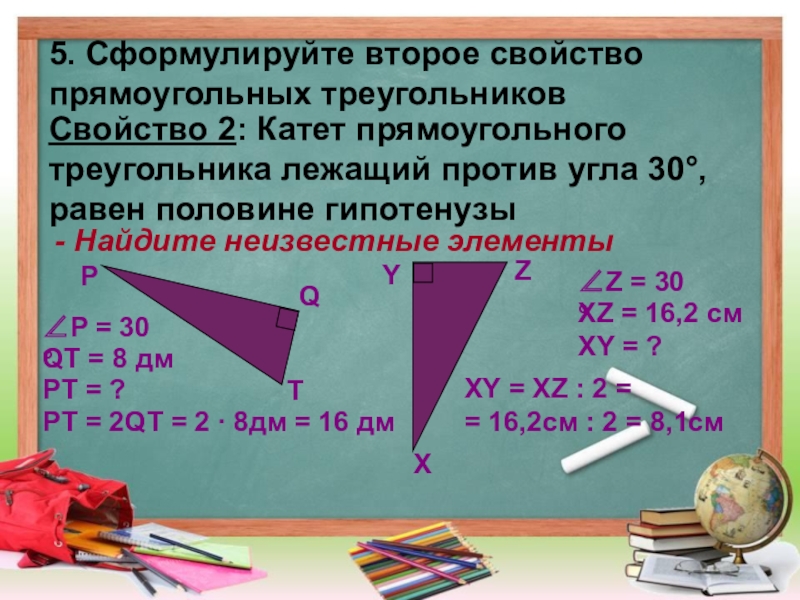
Слайд 55. Сформулируйте второе свойство
прямоугольных треугольников
Свойство 2: Катет прямоугольного
треугольника лежащий
равен половине гипотенузы
P
Q
T
∠P = 30 °
QT = 8 дм
PT = ?
- Найдите неизвестные элементы
PT = 2QT = 2 ∙ 8дм = 16 дм
Х
Y
Z
∠Z = 30 °
XZ = 16,2 см
XY = ?
XY = XZ : 2 =
= 16,2см : 2 = 8,1см
Слайд 66. Сформулируйте третье свойство
прямоугольных треугольников
Свойство 3: Если катет прямоугольного
треугольника
то угол, лежащий против этого катета
равен 30°.
- Найдите неизвестные элементы
O
T
K
3 cм
6 см
∠K = ?
∠T = ?
∠K = 30°
∠T = 90°- 30° = 60°
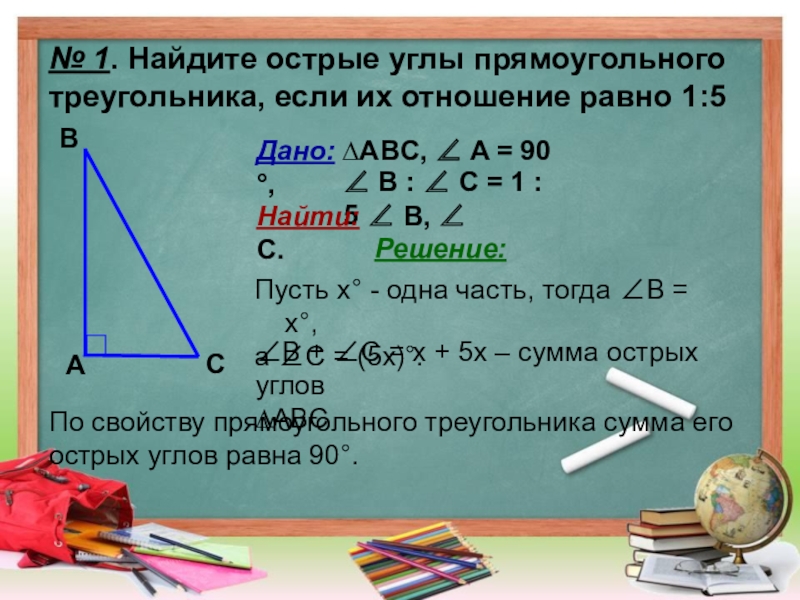
Слайд 7№ 1. Найдите острые углы прямоугольного
треугольника, если их отношение равно
А
B
C
Дано: ∆ABC, ∠ A = 90 °,
∠ B : ∠ C = 1 : 5
Найти: ∠ B, ∠ С.
Решение:
Пусть x° - одна часть, тогда ∠B = x°,
а ∠С = (5x)°.
По свойству прямоугольного треугольника сумма его острых углов равна 90°.
∠B + ∠C = x + 5x – сумма острых углов
∆ABC
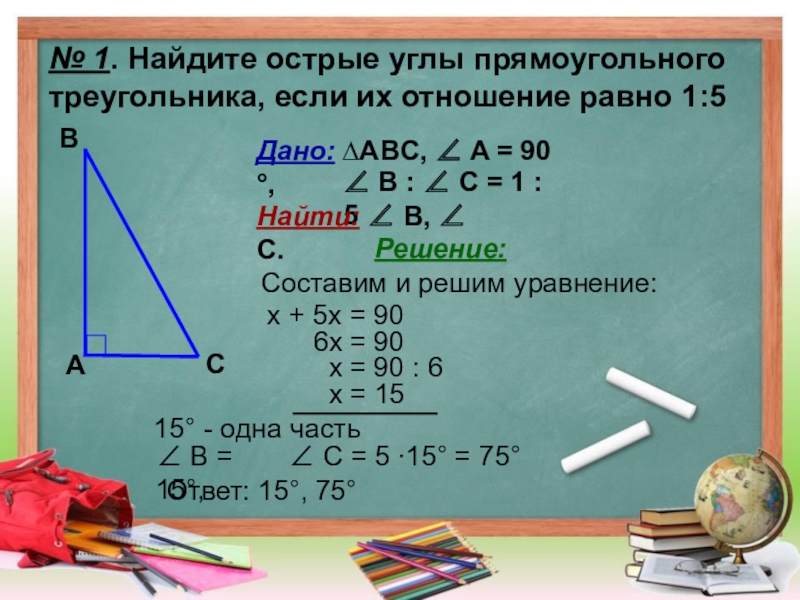
Слайд 8№ 1. Найдите острые углы прямоугольного
треугольника, если их отношение равно
А
B
C
Дано: ∆ABC, ∠ A = 90 °,
∠ B : ∠ C = 1 : 5
Найти: ∠ B, ∠ С.
Решение:
Составим и решим уравнение:
x + 5x = 90
6x = 90
x = 90 : 6
x = 15
15° - одна часть
∠ B = 15°,
∠ C = 5 ∙15° = 75°
Ответ: 15°, 75°
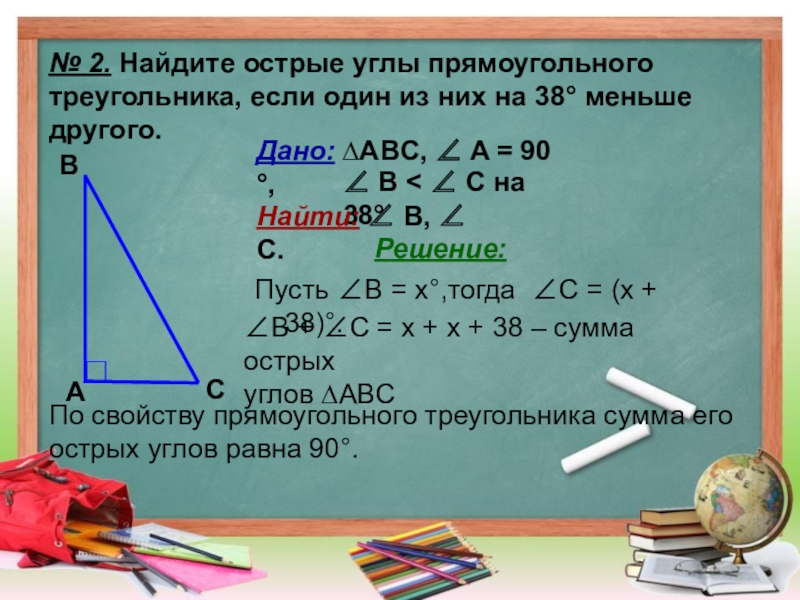
Слайд 9№ 2. Найдите острые углы прямоугольного
треугольника, если один из них
другого.
А
B
C
Дано: ∆ABC, ∠ A = 90 °,
∠ B < ∠ C на 38°
Найти: ∠ B, ∠ С.
Решение:
Пусть ∠B = x°,тогда ∠С = (x + 38)°.
По свойству прямоугольного треугольника сумма его острых углов равна 90°.
∠B + ∠C = x + x + 38 – сумма острых
углов ∆ABC
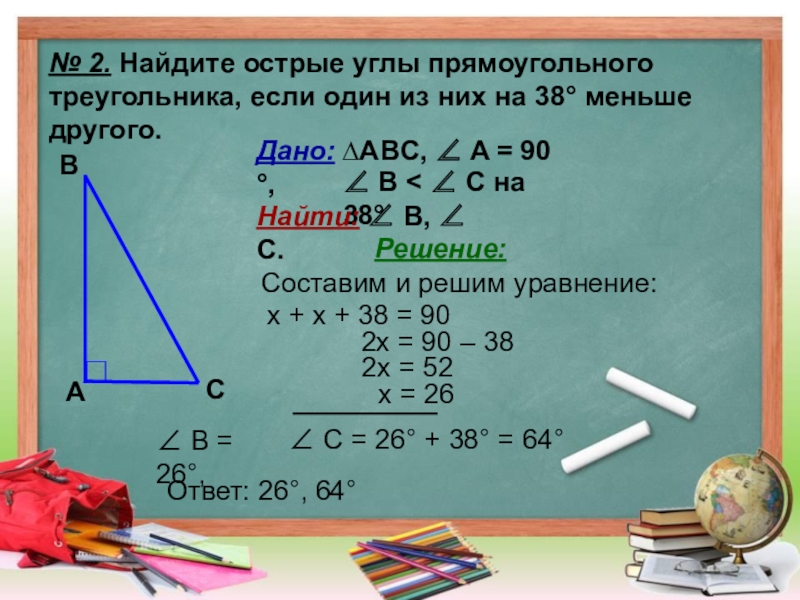
Слайд 10№ 2. Найдите острые углы прямоугольного
треугольника, если один из них
другого.
А
B
C
Дано: ∆ABC, ∠ A = 90 °,
∠ B < ∠ C на 38°
Найти: ∠ B, ∠ С.
Решение:
Составим и решим уравнение:
x + x + 38 = 90
2x = 90 – 38
2x = 52
x = 26
∠ B = 26°,
∠ C = 26° + 38° = 64°
Ответ: 26°, 64°
Слайд 11№ 259
(учебник Геометрия 7-9 Атанасян Л.С., стр.81)
Угол, противолежащий основанию равнобедренного
Слайд 12№ 259
(учебник Геометрия 7-9 Атанасян Л.С., стр.81)
Дано: ∆ABC, AB =
∠ B = 120°
CH | AB,
CH = 9 см
Найти: AC.
Решение:
1.Рассмотрим ∆CHА:∠H = 90°(по определению высоты),
значит ∆CHА – прямоугольный (по определению).
2. ∆ABC – равнобедренный => ∠A = ∠C
3. ∠A = ∠C = (180° - ∠B) : 2 = (180° - 120°) : 2 = 30° (по теореме о сумме углов треугольника)
A
B
C
120°
9 см
H
30°
4. AC = 2 ∙ CH = 2 ∙ 9 см = 18 см
Ответ: 18 см