- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Двугранный угол
Содержание
- 1. Презентация к уроку Двугранный угол
- 2. Цель урокаВвести понятие двугранного угла и его
- 3. Повторение1) Что называется углом на плоскости?
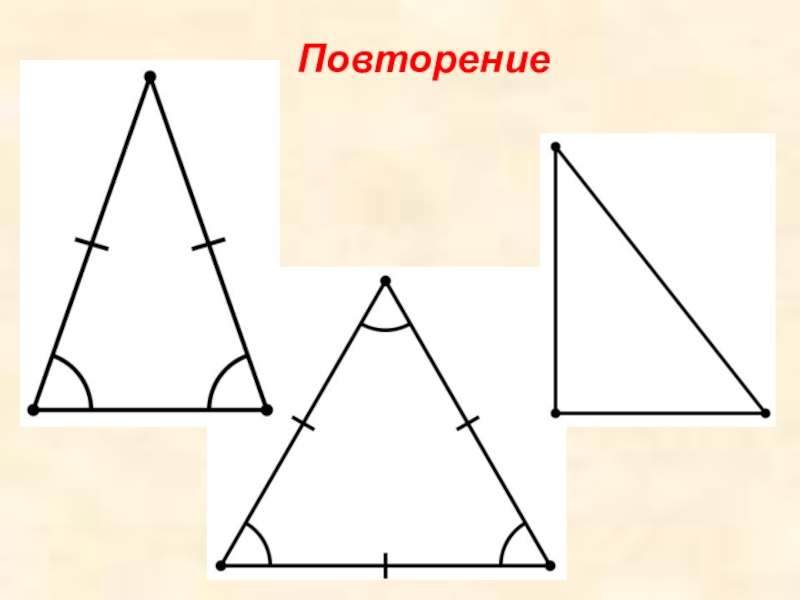
- 4. Повторение
- 5. ПланиметрияСтереометрияУглом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из одной точки.Двугранный угол
- 6. Двугранный угол.Знать и понимать: определение двугранного
- 7. Двугранным углом называется фигура, образованная прямой a
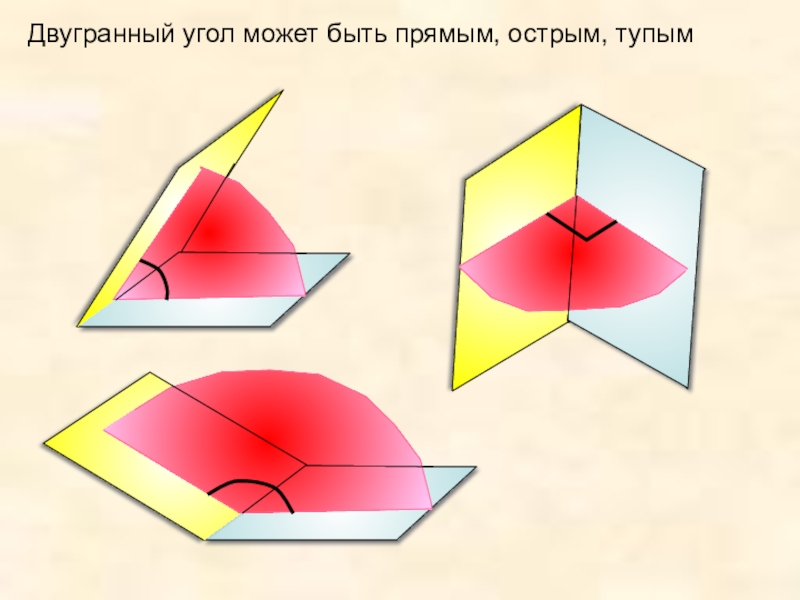
- 8. Двугранный угол может быть прямым, острым, тупым
- 9. Линейный угол двугранного углаЛинейным углом двугранного угла
- 10. Все линейные углы двугранного угла равны друг
- 11. Угол РDEK Двугранный угол АВNМ, где ВN
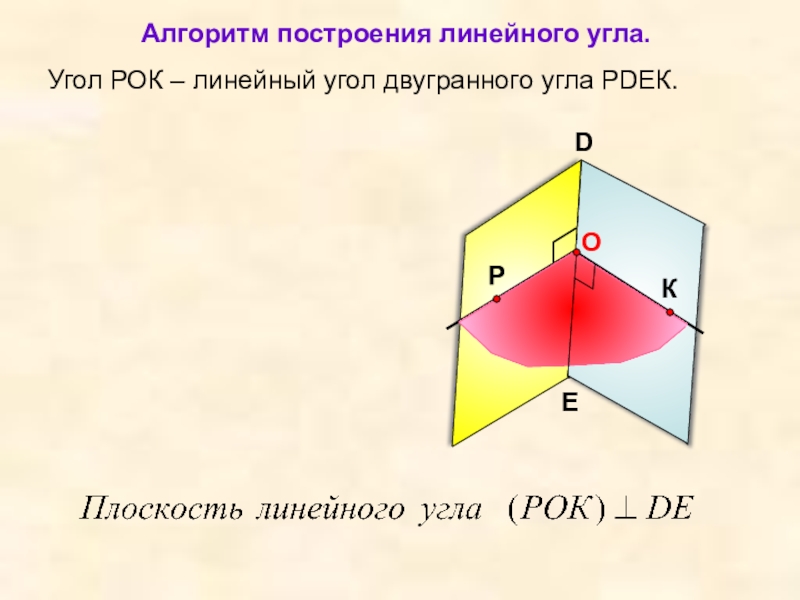
- 12. Угол РОК – линейный угол двугранного угла РDEК.DEАлгоритм построения линейного угла.
- 13. Теорема о трех перпендикулярах: Прямая, проведенная в
- 14. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – равнобедренный.АСВП-рН-яП-яУгол ВMN – линейный угол двугранного угла ВАСКК
- 15. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – прямоугольный.АВП-рН-яП-яУгол ВСN – линейный угол двугранного угла ВАСККС
- 16. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – тупоугольный.АВП-рН-яП-яУгол ВSN – линейный угол двугранного угла ВАСККС
- 17. Слайд 17
- 18. Тест „ Да и Нет не говорите,
- 19. Тест „ Да и Нет не говорите,
- 20. Домашнее задание: конспект урока; п. 22, № 167, № 168.
- 21. Построить линейный угол двугранного угла ВDСК.АВСD – прямоугольник.АВП-рН-яП-яУгол ВСN – линейный угол двугранного угла ВАСККСD
- 22. Построить линейный угол двугранного угла ВDСК.АВСD –
- 23. Построить линейный угол двугранного угла ВDСК.АВСD –
- 24. Построить линейный угол двугранного угла ВDСК.АВСD –
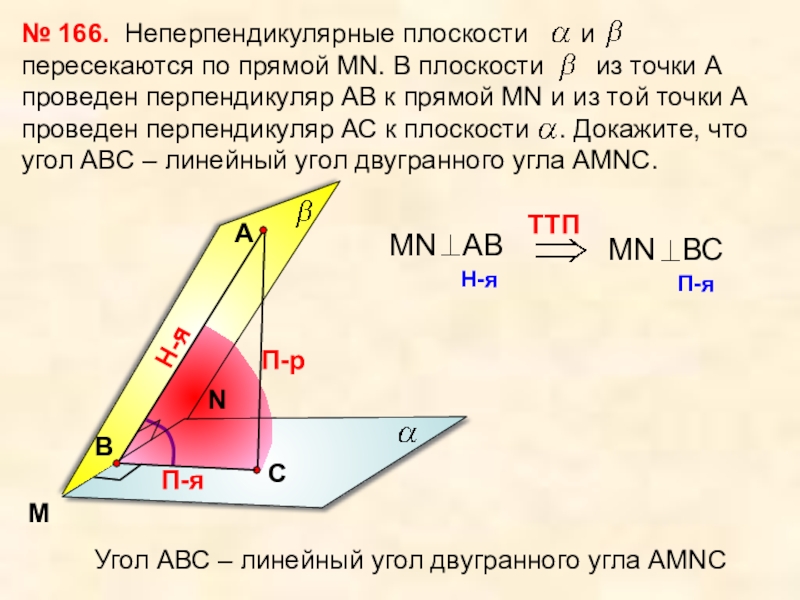
- 25. № 166.MNАП-рН-яП-яУгол АВС – линейный угол двугранного угла АМNC
- 26. САВDM
- 27. Слайд 27
- 28. Слайд 28
- 29. Двугранный угол.Знать и понимать: определение двугранного
Слайд 1Двугранный угол
10 класс
Геометрия
Учитель математики МКОУ «СОШ №7» г. Нальчик
Белоусова
Слайд 2Цель урока
Ввести понятие двугранного угла и его линейного угла
Рассмотреть задачи на
Сформировать конструктивный навык нахождения угла между плоскостями
Слайд 3Повторение
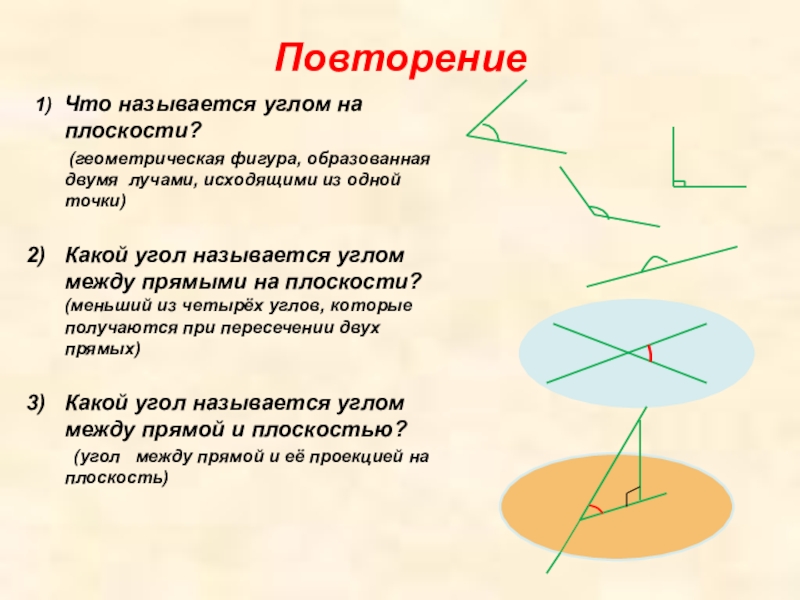
1) Что называется углом на плоскости?
(геометрическая
Какой угол называется углом между прямыми на плоскости? (меньший из четырёх углов, которые получаются при пересечении двух прямых)
Какой угол называется углом между прямой и плоскостью?
(угол между прямой и её проекцией на плоскость)
Слайд 5
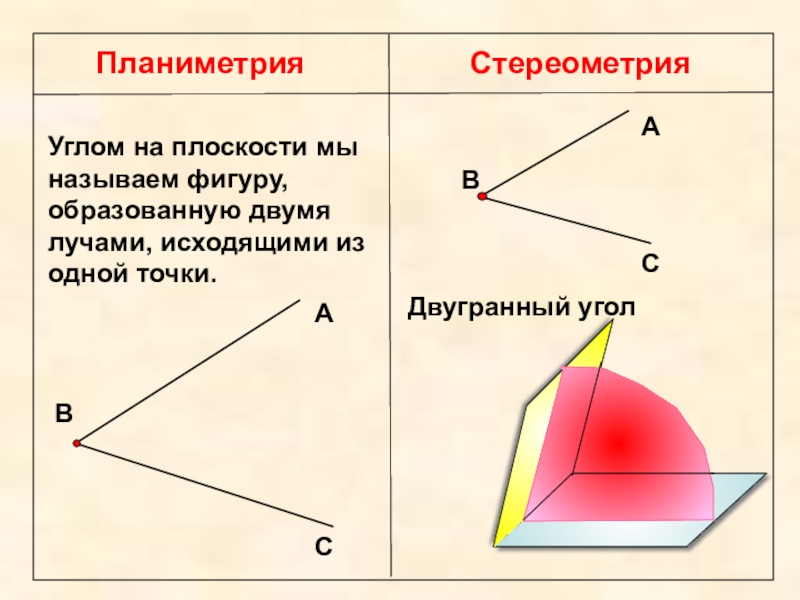
Планиметрия
Стереометрия
Углом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из
Двугранный угол
Слайд 6Двугранный угол.
Знать и понимать:
определение
двугранного угла,
как измерить
Уметь:
называть и обозначать
двугранный угол;
строить линейный угол двугранного угла;
находить величину двугранного угла.
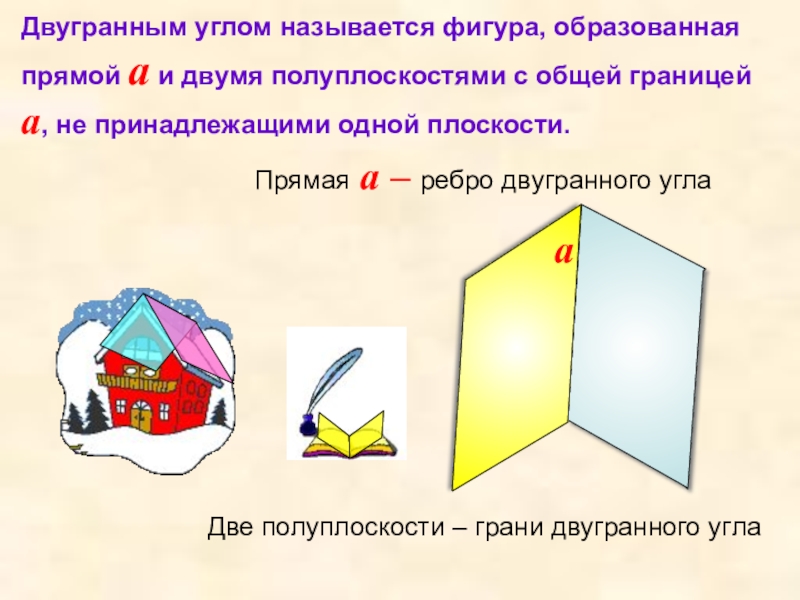
Слайд 7Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с
Две полуплоскости – грани двугранного угла
Прямая a – ребро двугранного угла
a
Слайд 9Линейный угол двугранного угла
Линейным углом двугранного угла называется угол между лучами,
Плоскость линейного угла перпендикулярна каждой грани двугранного угла
Градусной мерой двугранного угла называется градусная мера его линейного угла.
Слайд 10
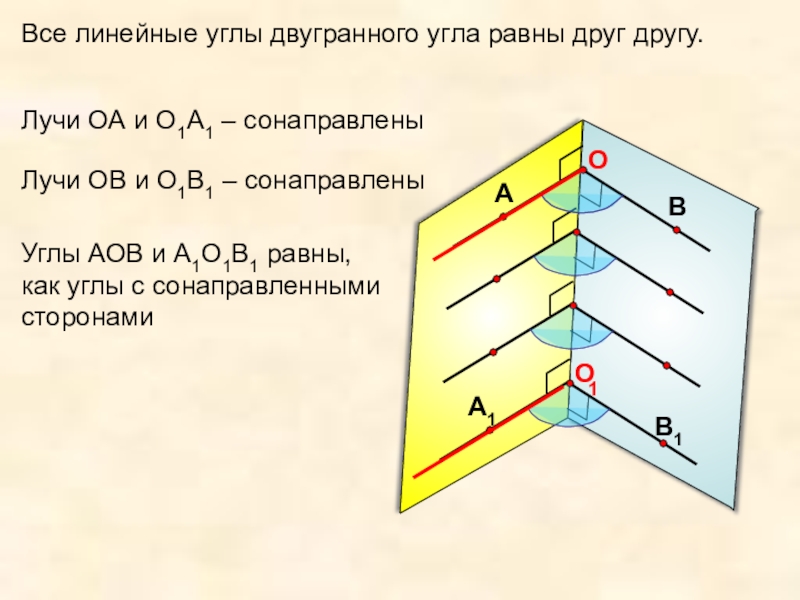
Все линейные углы двугранного угла равны друг другу.
1
Лучи ОА и О1А1
Лучи ОВ и О1В1 – сонаправлены
Углы АОВ и А1О1В1 равны,
как углы с сонаправленными сторонами
Слайд 11
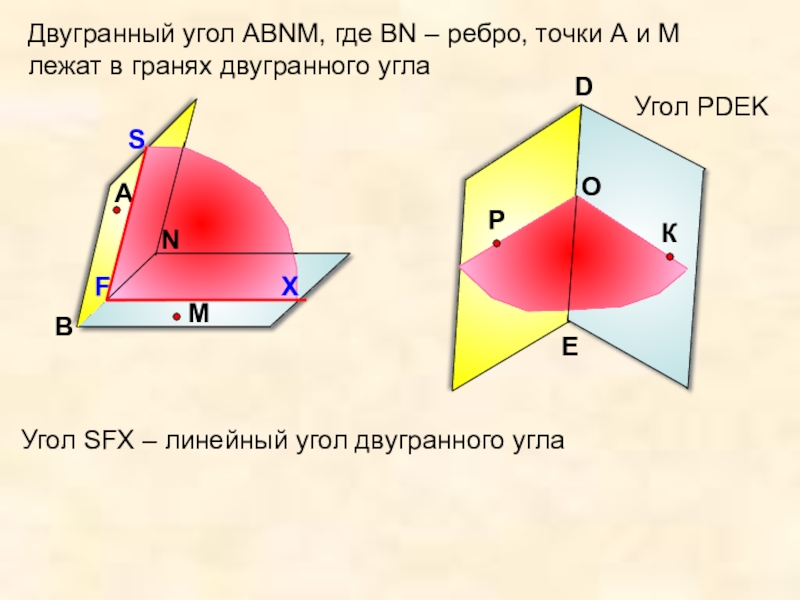
Угол РDEK
Двугранный угол АВNМ, где ВN – ребро, точки А
А
В
N
Р
M
К
D
E
Угол SFX – линейный угол двугранного угла
Слайд 13
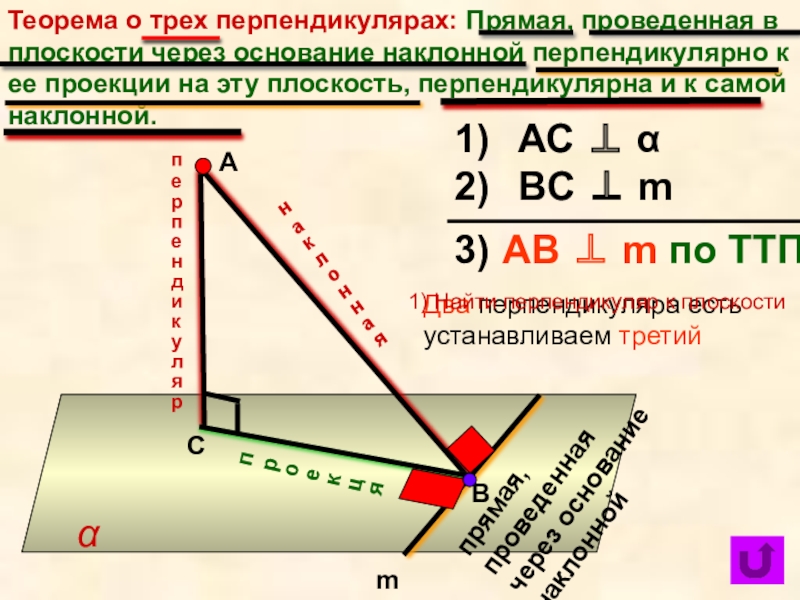
Теорема о трех перпендикулярах: Прямая, проведенная в плоскости через основание наклонной
α
А
С
В
п
е
р
п
е
н
д
и
к
у
л
я
р
н
а
к
л
о
н
н
а
я
п
р
о
е
к
ц
я
прямая, проведенная через основание наклонной
1)
2)
3)
АС ⊥ α
m
BС ⊥ m
АB ⊥ m по ТТП
Два перпендикуляра есть устанавливаем третий
1) Найти перпендикуляр к плоскости
Слайд 14
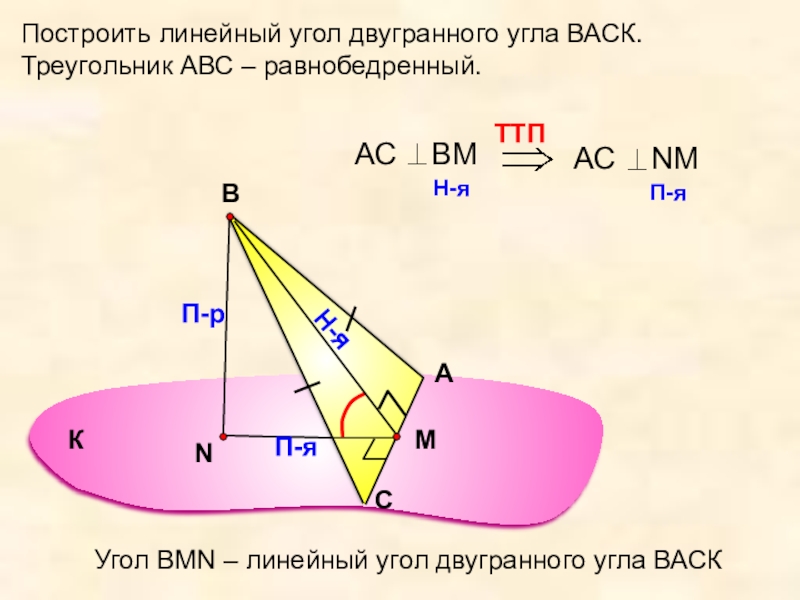
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
А
С
В
П-р
Н-я
П-я
Угол ВMN –
К
Слайд 15
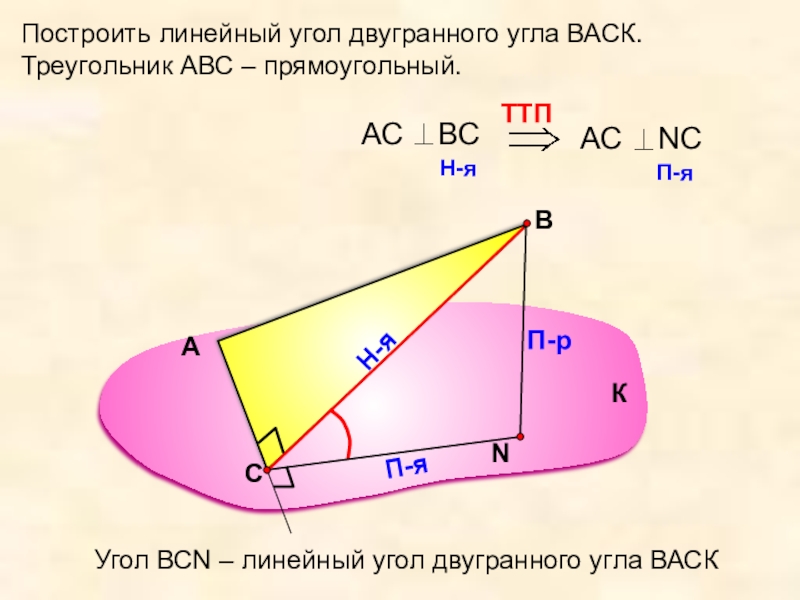
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
А
В
П-р
Н-я
П-я
Угол ВСN –
К
С
Слайд 16
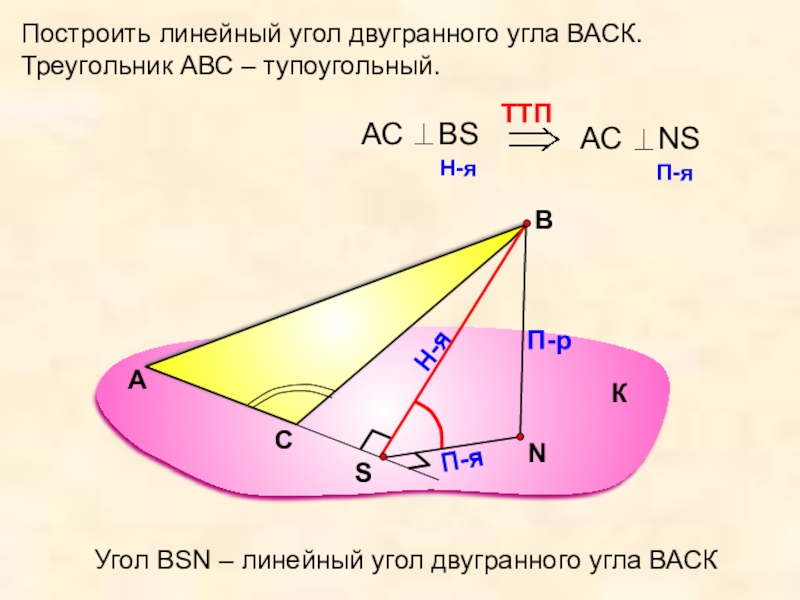
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
А
В
П-р
Н-я
П-я
Угол ВSN –
К
С
Слайд 17
1) Какой угол называется двугранным?
2) Назовите двугранный угол.
3) Назовите ребро двугранного угла.
4) Назовите грани двугранного угла.
5) Назовите линейный угол двугранного угла.
6) Каким свойством обладают линейные углы двугранного угла?
7) Как построить линейный угол двугранного угла?
8) Чему равна градусная мера двугранного угла?
Тест „ Проверь себя“
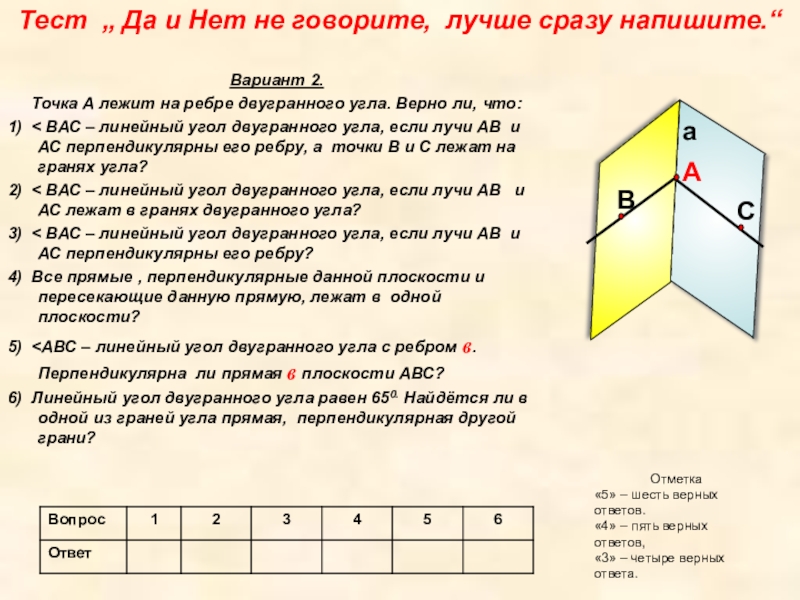
Слайд 18Тест „ Да и Нет не говорите, лучше сразу напишите.“
Вариант 1.
Точка
1) < ВАС – линейный угол двугранного угла, если лучи АВ и АС перпендикулярны его ребру?
2) < ВАС – линейный угол двугранного угла, если лучи АВ и АС лежат в гранях двугранного угла?
3) < ВАС – линейный угол двугранного угла, если лучи АВ и АС перпендикулярны его ребру,
а точки В и С лежат на гранях угла?
4) Линейный угол двугранного угла равен 800. Найдётся ли в одной из граней угла прямая, перпендикулярная другой грани?
5) <АВС – линейный угол двугранного угла с ребром a. Перпендикулярна ли прямая а плоскости АВС?
6) Верно ли, что все прямые, перпендикулярные данной плоскости и пересекающие данную
прямую, лежат в одной плоскости?
Отметка
«5» – шесть верных ответов.
«4» – пять верных ответов,
«3» – четыре верных ответа.
Слайд 19Тест „ Да и Нет не говорите, лучше сразу напишите.“
Вариант 2.
Точка
1) < ВАС – линейный угол двугранного угла, если лучи АВ и АС перпендикулярны его ребру, а точки В и С лежат на гранях угла?
2) < ВАС – линейный угол двугранного угла, если лучи АВ и АС лежат в гранях двугранного угла?
3) < ВАС – линейный угол двугранного угла, если лучи АВ и АС перпендикулярны его ребру?
4) Все прямые , перпендикулярные данной плоскости и пересекающие данную прямую, лежат в одной плоскости?
5) <АВС – линейный угол двугранного угла с ребром в. Перпендикулярна ли прямая в плоскости АВС?
6) Линейный угол двугранного угла равен 650. Найдётся ли в одной из граней угла прямая, перпендикулярная другой грани?
Отметка
«5» – шесть верных ответов.
«4» – пять верных ответов,
«3» – четыре верных ответа.
Слайд 21
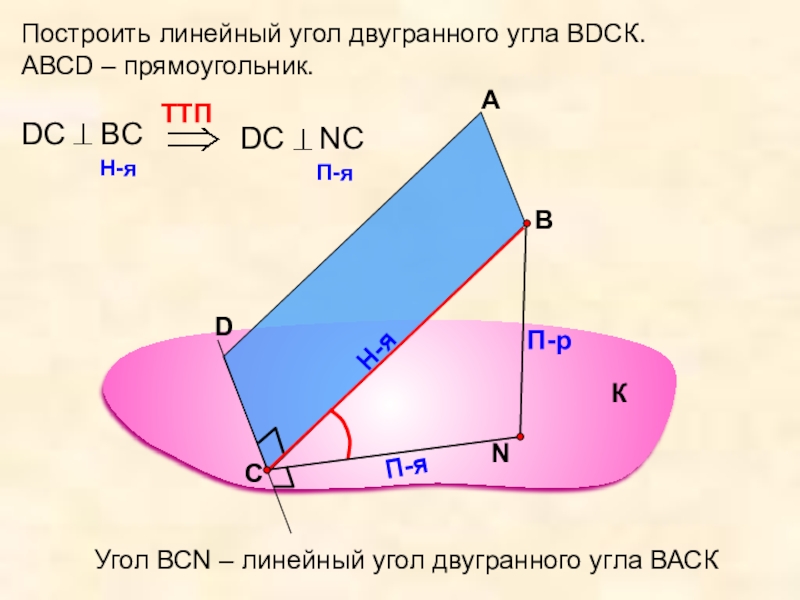
Построить линейный угол двугранного угла ВDСК.
АВСD – прямоугольник.
А
В
П-р
Н-я
П-я
Угол ВСN – линейный
К
С
D
Слайд 22
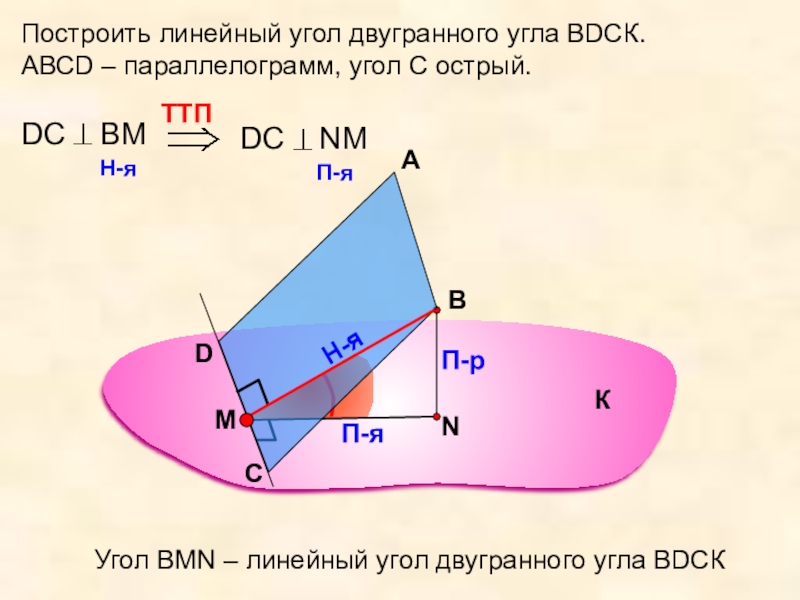
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С острый.
А
В
П-р
П-я
Угол
К
С
D
Н-я
Слайд 23
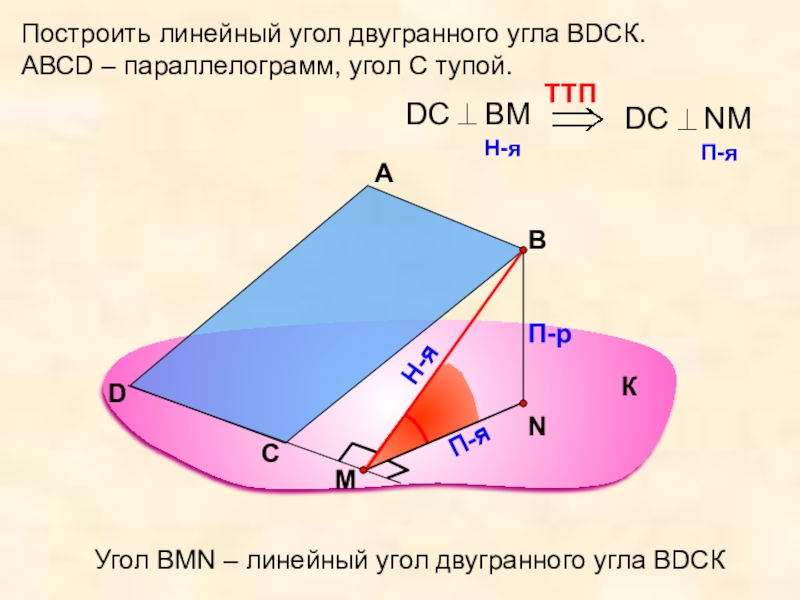
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С тупой.
А
В
П-р
П-я
Угол
К
С
D
Н-я
Слайд 24
Построить линейный угол двугранного угла ВDСК.
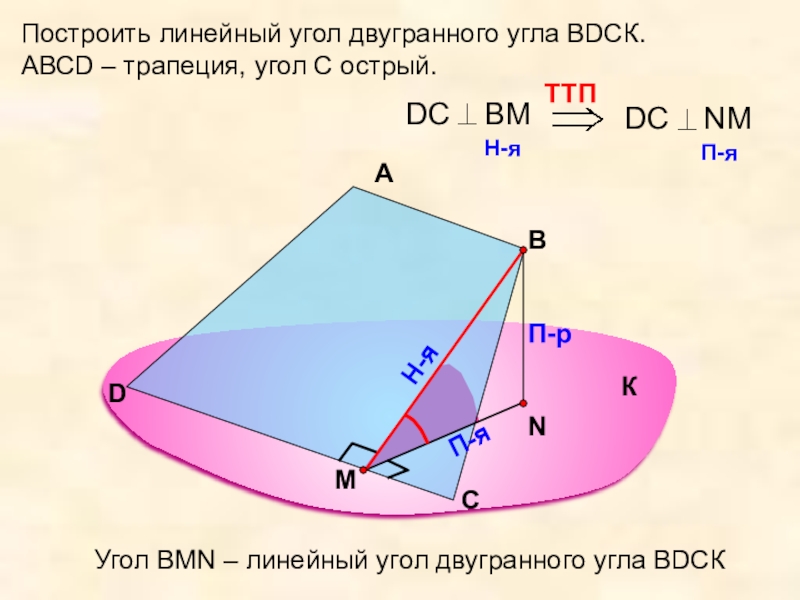
АВСD – трапеция, угол С острый.
А
В
П-р
П-я
Угол
К
С
D
Н-я
Слайд 26
С
А
В
D
M
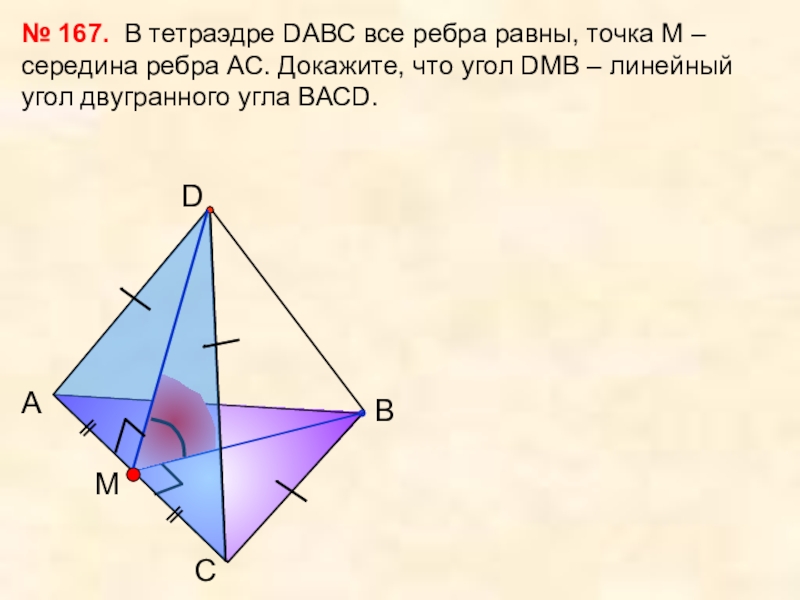
В тетраэдре DАВС все
№ 167.
Слайд 27 Двугранный угол равен
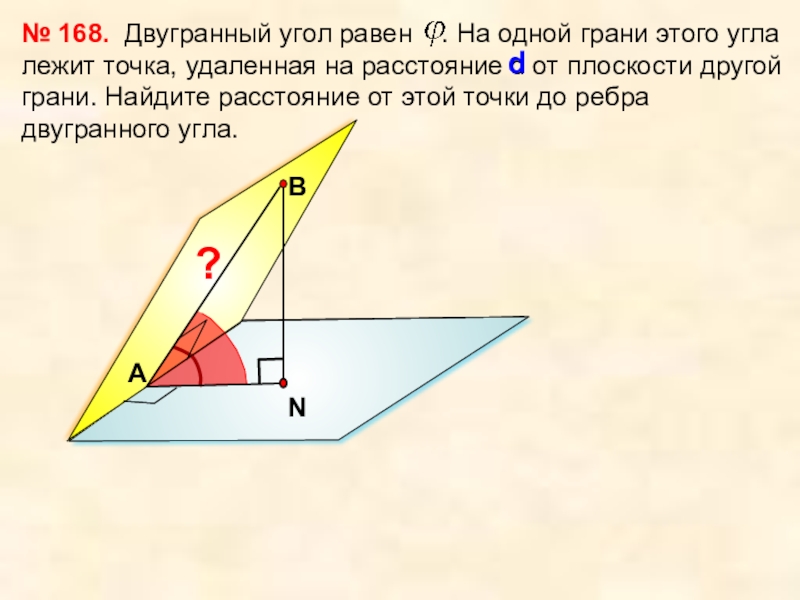
№ 168.
В
d
А
?
Слайд 28
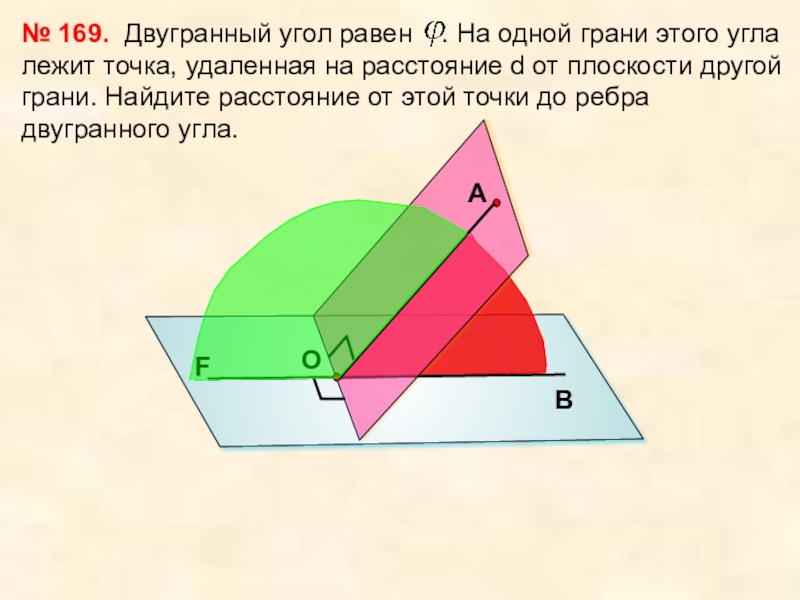
Двугранный угол равен
№ 169.
А
Слайд 29Двугранный угол.
Знать и понимать:
определение
двугранного угла,
как измерить
Уметь:
называть и обозначать
двугранный угол;
строить линейный угол двугранного угла;
находить величину двугранного угла.