Составила учитель математики МБОУ «Мурминская СШ» Рязанской области Ефименко Лидия Михайловна.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры на тему Область допустимых значений при решении уравнений
Содержание
- 1. Презентация к уроку алгебры на тему Область допустимых значений при решении уравнений
- 2. Слайд 2
- 3. Какие приемы можно использовать для решения уравнений?1)
- 4. Приемы решения тригонометрических уравнений:замена переменной;приведение к одной
- 5. Какое уравнение нами не до конца отработано?1)
- 6. Сформулируйте тему сегодняшнего урока.
- 7. Область допустимых значений при решении уравнений.Урок решения ключевых задач.
- 8. Какова же цель урока?
- 9. Уметь решать уравнения,в которых областью допустимых значений
- 10. №1 ctgx-ctgxcosx=0ctgx(1-cosx)=0
- 11. ctgx-ctgxcosx=0ctgx(1-cosx)=0
- 12. ctgx-ctgxcosx=0ctgx(1-cosx)=0
- 13. ctgx-ctgxcosx=0ctgx(1-cosx)=0
- 14. №2(sinx+cosx)√9-x²=0
- 15. (sinx+cosx)√9-x²=0(sinx+cosx)=0 или
- 16. (sinx+cosx)√9-x²=0(sinx+cosx)=0 или
- 17. (sinx+cosx)√9-x²=0(sinx+cosx)=0 или
- 18. (sinx+cosx)√9-x²=0(sinx+cosx)=0 или
- 19. (sinx+cosx)√9-x²=0(sinx+cosx)=0 или
- 20. №3(√3tgx+1)√-17cosx=0
- 21. (√3tgx+1)√-17cosx=0√3tgx+1=0 или
- 22. (√3tgx+1)√-17cosx=0√3tgx+1=0 или
- 23. (√3tgx+1)√-17cosx=0√3tgx+1=0 или
- 24. (√3tgx+1)√-17cosx=0√3tgx+1=0 или
- 25. (√3tgx+1)√-17cosx=0√3tgx+1=0 или
- 26. №4(sin2x-cosx)√πх-х²=0
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. x= π/6+2πn/3, nϵz
- 34. x= π/6+2πn/3, nϵz
- 35. x= π/6+2πn/3, nϵz
- 36. x= π/6+2πn/3, nϵz
- 37. x= π/6+2πn/3, nϵz
- 38. Что нового вы сегодня узнали?сtgx-ctgxcosx=0(sinx+cosx) √3x-x²=0(√3tgx+1)√-17cosx=0(sin2x-cosx) √πх-х²=0
- 39. Осознанно понимаете высказывание:«Произведение равно 0, если хотя
- 40. Практикум: №18.33 №18.34
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Спасибо за урок.
Какие приемы можно использовать для решения уравнений?1) 6cos²x+cosx-1=0 2) 8sin²2x+cos2x+1=0 3) 2tgx-3ctgx+5=0 4) tg3x-tg²3x=0
Слайд 3Какие приемы можно использовать для решения уравнений?
1) 6cos²x+cosx-1=0
2) 8sin²2x+cos2x+1=0
3) 2tgx-3ctgx+5=0
4) tg3x-tg²3x=0
5) 2sin²x-5sinxcosx+2cos²x=0
6) 3sin²x- sinxcosx=2
7) sin2x=cos2x
8) sin²x-sinxcosx=0
9) ctgx-ctgxcosx=0
Слайд 4Приемы решения тригонометрических уравнений:
замена переменной;
приведение к одной функции;
разложение на множители левой
части, чтобы правая часть была равна нулю;
однородные уравнения.
однородные уравнения.
Слайд 5Какое уравнение нами не до конца отработано?
1) 6cos²x+cosx-1=0
2) 8sin²2x+cos2x+1=0
3) 2tgx-3ctgx+5=0
4) tg3x-tg²3x=0
5) 2sin²x-5sinxcosx+2cos²x=0
6) 3sin²x- sinxcosx=2
7) sin2x=cos2x
8) sin²x-sinxcosx=0
9) ctgx-ctgxcosx=0
Слайд 9
Уметь решать уравнения,в которых областью допустимых значений не являются все числа.
Рассмотреть способы решения таких уравнений.
Подготовка к ЕГЭ.
Подготовка к ЕГЭ.
Слайд 12
ctgx-ctgxcosx=0
ctgx(1-cosx)=0 О.Д.З. х≠πn, nϵz
ctgx=0
или 1-cosx=0
х=π/2+πn, nϵz сosх=1
х=2πn, nϵz
х=π/2+πn, nϵz сosх=1
х=2πn, nϵz
Слайд 13
ctgx-ctgxcosx=0
ctgx(1-cosx)=0 О.Д.З. х≠πn, nϵz
ctgx=0
или 1-cosx=0
х=π/2+πn, nϵz cosх=1
х=2πn, nϵz
(не соотв. О.Д.З.)
Ответ: π/2+πn, nϵz
ЕГЭ: 1) 2πn; 2) 2πn; π/2+πn, 3) π/2+πn,
х=π/2+πn, nϵz cosх=1
х=2πn, nϵz
(не соотв. О.Д.З.)
Ответ: π/2+πn, nϵz
ЕГЭ: 1) 2πn; 2) 2πn; π/2+πn, 3) π/2+πn,
Слайд 16(sinx+cosx)√9-x²=0
(sinx+cosx)=0 или √9-x²=0
(3-х)(3+х)≥0
(3-х)(3+х)=0
tgx+1=0 х=3 или х=-3
-3≤x≤3
tgx+1=0 х=3 или х=-3
-3≤x≤3
Слайд 17(sinx+cosx)√9-x²=0
(sinx+cosx)=0 или √9-x²=0
(3-х)(3+х)≥0
(3-х)(3+х)=0
tgx+1=0 х=-3 или х=3
-3≤x≤3
х=-π/4+πn, nϵz
-3≤x≤3
tgx+1=0 х=-3 или х=3
-3≤x≤3
х=-π/4+πn, nϵz
-3≤x≤3
Слайд 18(sinx+cosx)√9-x²=0
(sinx+cosx)=0 или √9-x²=0
(3-х)(3+х)≥0
(3-х)(3+х)=0
tgx+1=0 х=3 или х=-3
-3≤x≤3
х=-π/4+πn, nϵz 3π/4
-3≤x≤3
tgx+1=0 х=3 или х=-3
-3≤x≤3
х=-π/4+πn, nϵz 3π/4
-3≤x≤3
-π/4
х
у
3
-3
Слайд 19(sinx+cosx)√9-x²=0
(sinx+cosx)=0 или √9-x²=0
(3-х)(3+х)≥0
(3-х)(3+х)=0
tgx+1=0 х=3 или х=-3
-3≤x≤3
х=-π/4+πn, nϵz 3π/4
-3≤x≤3
х=3π/4; х=-π/4
Ответ: 0; 3; 3π/4; -π/4
ЕГЭ: 1)3π/4; 2) 0; 3; 3)-π/4+πn; 0; 3 4) 0; 3; 3π/4;-π/4
tgx+1=0 х=3 или х=-3
-3≤x≤3
х=-π/4+πn, nϵz 3π/4
-3≤x≤3
х=3π/4; х=-π/4
Ответ: 0; 3; 3π/4; -π/4
ЕГЭ: 1)3π/4; 2) 0; 3; 3)-π/4+πn; 0; 3 4) 0; 3; 3π/4;-π/4
0
3
-π/4
х
у
-3
Слайд 23(√3tgx+1)√-17cosx=0
√3tgx+1=0 или √-17cosx =0
-17cosx≥0 cosx≠0
tgx=-√3/3 Нет решений.
cosx≤0
x=-π/6+πn, nϵz
cosx<0
Слайд 24(√3tgx+1)√-17cosx=0
√3tgx+1=0 или √-17cosx =0
-17cosx≥0 cosx≠0
tgx=-√3/3 Нет решений.
cosx≤0
x=-π/6+πn, nϵz 5π/6
cosx<0 -π/6
х
у
Слайд 25(√3tgx+1)√-17cosx=0
√3tgx+1=0 или √-17cosx =0
-17cosx≥0 cosx≠0
tgx=-√3/3 Нет решений.
cosx≤0
x=-π/6+πn, nϵz
cosx<0
x=5π/6+2πn, nϵz
Ответ: 5π/6+2πn, nϵz
Слайд 29
№4
(sin2x-cosx)√πх-х²=0
sin2x=cosx или √πх-х²=0
x(π-х)≥0 x(π-х)=0
sin2x=sin(π/2-x) x=0 или x=π
0≤x≤π
(sin2x-cosx)√πх-х²=0
sin2x=cosx или √πх-х²=0
x(π-х)≥0 x(π-х)=0
sin2x=sin(π/2-x) x=0 или x=π
0≤x≤π
Слайд 30
№4
(sin2x-cosx)√πх-х²=0
sin2x-cosx=0 или √πх-х²=0
x(π-х)≥0 x(π-х)=0
sin2x=sin(π/2-x) x=0 или x=π
0≤x≤π
2x=arcsin(sin(π/2-x)+2πn
2х=π-arcsin(sin(π/2-x)+2πn
0≤x≤π
(sin2x-cosx)√πх-х²=0
sin2x-cosx=0 или √πх-х²=0
x(π-х)≥0 x(π-х)=0
sin2x=sin(π/2-x) x=0 или x=π
0≤x≤π
2x=arcsin(sin(π/2-x)+2πn
2х=π-arcsin(sin(π/2-x)+2πn
0≤x≤π
Слайд 31
№4
(sin2x-cosx)√πх-х²=0
sin2x-cosx=0 или √πх-х²=0
x(π-х)≥0 x(π-х)=0
sin2x=sin(π/2-x) x=0 или x=π
0≤x≤π
2x=π/2-x+2πn, nϵz или 2х=π-(π/2-x)+2πn, nϵz
0≤x≤π 0≤x≤π
(sin2x-cosx)√πх-х²=0
sin2x-cosx=0 или √πх-х²=0
x(π-х)≥0 x(π-х)=0
sin2x=sin(π/2-x) x=0 или x=π
0≤x≤π
2x=π/2-x+2πn, nϵz или 2х=π-(π/2-x)+2πn, nϵz
0≤x≤π 0≤x≤π
Слайд 32
№4
(sin2x-cosx)√πх-х²=0
sin2x-cosx=0 или √πх-х²=0
x(π-х)≥0 x(π-х)=0
sin2x=sin(π/2-x) x=0 или x=π
0≤x≤π
2x=π/2-x+2πn, nϵz или 2х=π-(π/2-x)+2πn,nϵz
0≤x≤π 0≤x≤π
3x=π/2+2πn, nϵz x=π/2+2πn, nϵz
0≤x≤π 0≤x≤π
(sin2x-cosx)√πх-х²=0
sin2x-cosx=0 или √πх-х²=0
x(π-х)≥0 x(π-х)=0
sin2x=sin(π/2-x) x=0 или x=π
0≤x≤π
2x=π/2-x+2πn, nϵz или 2х=π-(π/2-x)+2πn,nϵz
0≤x≤π 0≤x≤π
3x=π/2+2πn, nϵz x=π/2+2πn, nϵz
0≤x≤π 0≤x≤π
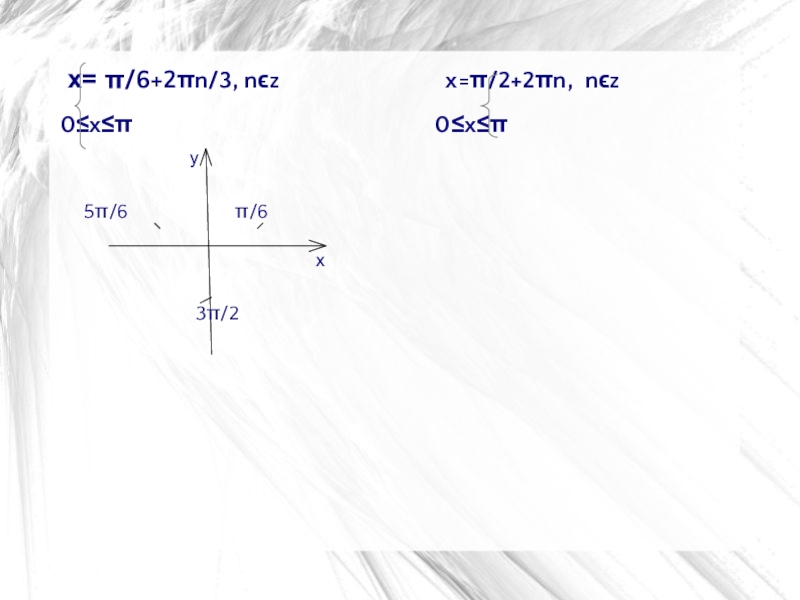
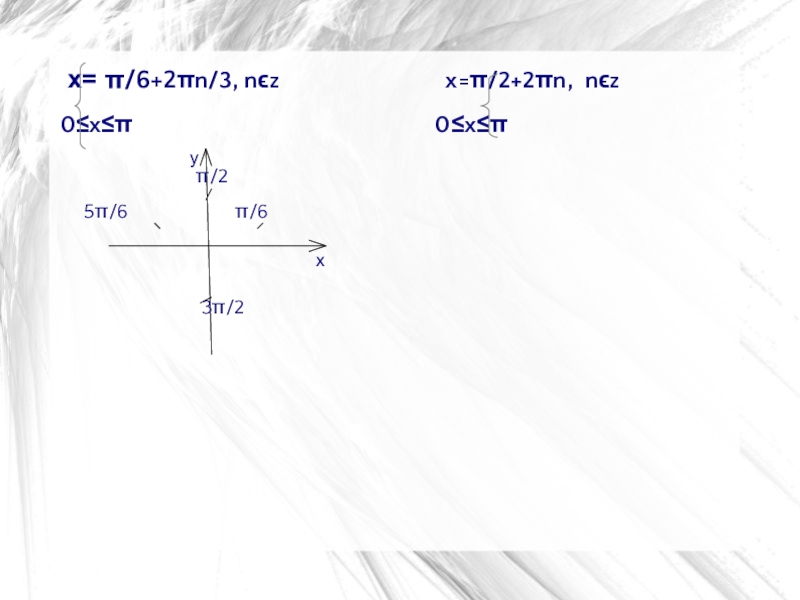
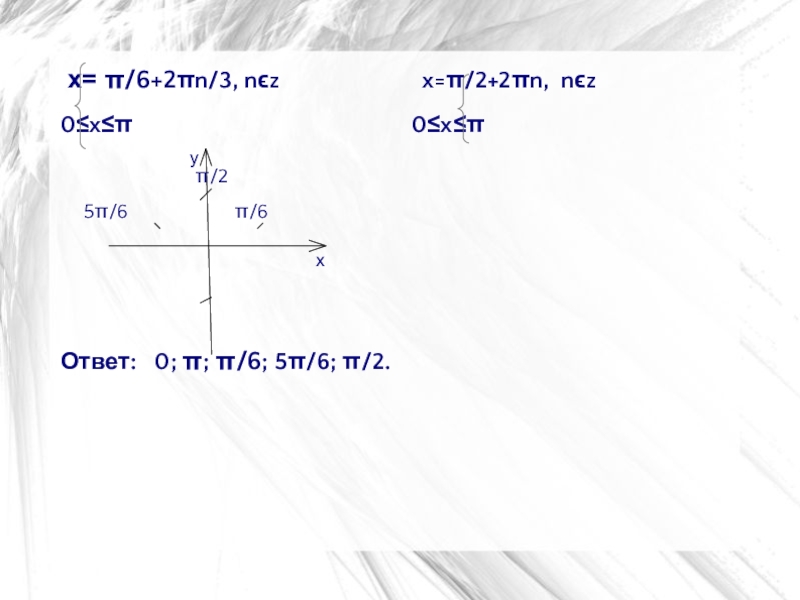
Слайд 37 x= π/6+2πn/3, nϵz
x=π/2+2πn, nϵz
0≤x≤π 0≤x≤π
0≤π/6+2πn/3≤π 0≤ π/2+2πn≤π
-π/6≤2πn/3≤5π/6 -1/2≤2n≤1/2
-1/6≤2n/3≤5/6 -1/4≤ n≤1/4
-1/2≤2n≤5/2 n=0; х=π/2
-1/4≤n≤5/4, nϵz
n=0; 1 х=π/6; х=5π/6
Ответ: 0; π; π/6; 5π/6; π/2.
0≤x≤π 0≤x≤π
0≤π/6+2πn/3≤π 0≤ π/2+2πn≤π
-π/6≤2πn/3≤5π/6 -1/2≤2n≤1/2
-1/6≤2n/3≤5/6 -1/4≤ n≤1/4
-1/2≤2n≤5/2 n=0; х=π/2
-1/4≤n≤5/4, nϵz
n=0; 1 х=π/6; х=5π/6
Ответ: 0; π; π/6; 5π/6; π/2.
Слайд 38Что нового вы сегодня узнали?
сtgx-ctgxcosx=0
(sinx+cosx) √3x-x²=0
(√3tgx+1)√-17cosx=0
(sin2x-cosx) √πх-х²=0
Слайд 39Осознанно понимаете высказывание:
«Произведение равно 0, если хотя бы один из множителей
равен 0, а другой при этом не теряет смысла».
При решении уравнений надо обязательно учитывать область допустимых значений переменной и с учетом ее правильно записать ответ.
При решении уравнений надо обязательно учитывать область допустимых значений переменной и с учетом ее правильно записать ответ.
