- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к учебному проекту на тему Аксиома. Что это?
Содержание
- 1. Презентация к учебному проекту на тему Аксиома. Что это?
- 2. «Аксиомы обладают наивысшей степенью общности и представляют начало всего»Аристотель (древнегреческий философ, 384-322 гг. до н.э.)
- 3. Цели проекта:Узнать, что такое аксиома.Сравнить аксиомы Евклида
- 4. Гипотеза проекта: Проводя исследование по выбранной
- 5. В переводе с
- 6. Начальные геометрические знания были добыты
- 7. К III в до н.э.
- 8. Слайд 8
- 9. Ватиканский манускрипт (XI, Предложения, 31—33)Классический труд Евклида,
- 10. АКСИОМА – утверждение, не требующее доказательства.Слово «аксиома»
- 11. АКСИОМЫ ЕВКЛИДА1. Равные одному и тому же
- 12. ПОСТУЛАТ – утверждение не требующее доказательства (аксиомы
- 13. ПОСТУЛАТЫ ЕВКЛИДА I.
- 14. Пятый постулат ЕвклидаНа современном языке: Если
- 15. Пятый постулат ЕвклидаВ школьных учебниках: Через
- 16. Слайд 16
- 17. «Чем отличается геометрия Лобачевского от геометрии Евклида?» Главное различие кроется в понимании самой природы пространства:
- 18. «Новая геометрия» Николая ЛобачевскогоГиперболический параболоидВоронка Как показали
- 19. ВЫВОД Несмотря на кажущиеся странности, геометрия
- 20. Аксиомы планиметрииКакова бы ни была прямая, существуют
- 21. Аксиомы стереометрииЧерез любые три точки, не лежащие
- 22. Фридрих Бернхард Риман (1826-1866)
- 23. АКСИОМЫ В АЛГЕБРЕСвойства сложенияa+b=b+aa+(b+c)=(a+b)+cСвойства умноженияab=baa(bc)=(ab)ca(b+c)=ab+ac
- 24. АКСИОМЫ В ФИЗИКЕ
- 25. ОСНОВНЫЕ АКСИОМЫ БИОЛОГИИАксиома 1. Все живые организмы
- 26. АКСИОМЫ В ФИЛОСОФИИЧтобы правильно построить философию, необходимо
- 27. АКСИОМЫ В ГЕОГРАФИИАксиома Григорьева А.А. о географической
- 28. АКСИОМЫ ЭКОЛОГИИ ЧЕЛОВЕКААксиома экологии человека 1: эволюция
- 29. У каждого свой исходный постулат,
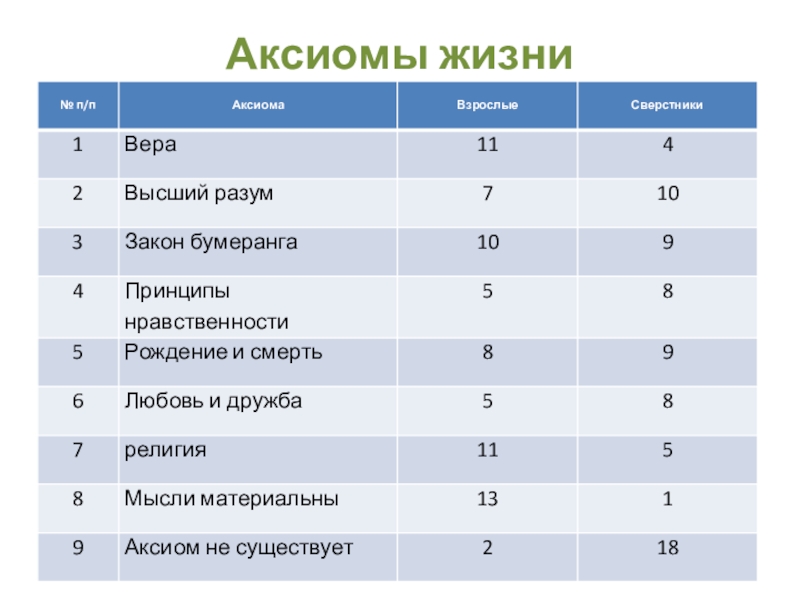
- 30. Аксиомы жизни
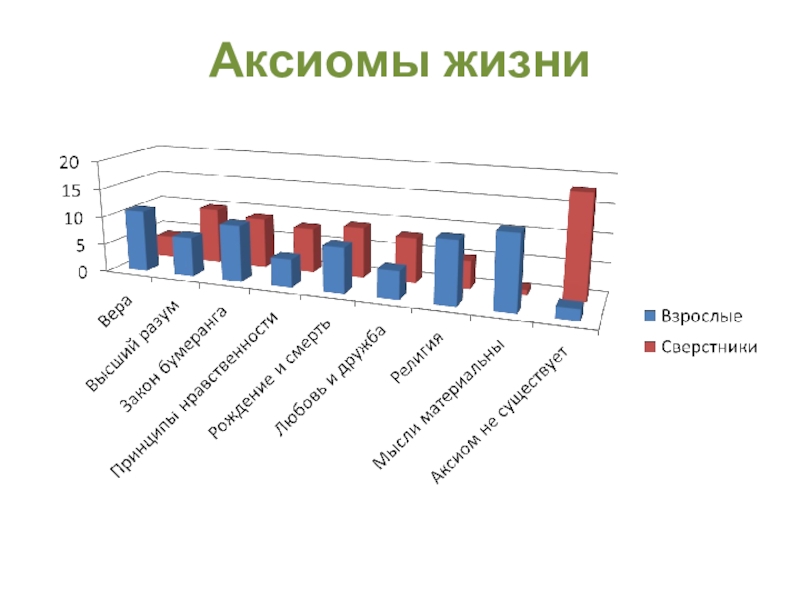
- 31. Аксиомы жизни
- 32. Аксиома жизни Трикими В
- 33. Спасибо за внимание!
Слайд 1Учебный проект на тему:
«Аксиома. Что это?»
Выполнили:
ученики 7 класса А
Сапсуева Маргарита
Экес
Учитель-консультант:
Поспелова Е.А.
МБОУ СОШ № 3 им. Героя России
Сергея Ромашина
г. Южно-Сахалинск, 2017 г.
Слайд 2«Аксиомы обладают наивысшей степенью общности и представляют начало всего»
Аристотель
(древнегреческий философ,
384-322 гг. до н.э.)
Слайд 3Цели проекта:
Узнать, что такое аксиома.
Сравнить аксиомы Евклида и Лобачевского.
Найти аксиомы в
Провести опрос среди сверстников и взрослых: «Какие аксиомы сопутствуют в жизни?».
Сформировать исследовательские и презентационные умения и навыки.
Слайд 4Гипотеза проекта:
Проводя исследование по выбранной теме, мы можем предположить,
Слайд 5 В переводе с греческого слово ГЕОМЕТРИЯ означает
Такое название объясняется тем, что зарождение геометрии было связано с различными измерительными работами
Слайд 6 Начальные геометрические знания были добыты опытным путем. Получение новых
Слайд 7 К III в до н.э. геометрия становится дедуктивной наукой,
Слайд 8
Евклид –
О самом Евклиде практически ничего не известно. «Точные» же биографические данные основываются на заметках неизвестного арабского математика XII века: «Евклид, сын Наукрата, известный под именем «Геометра», учёный старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира…»
Слайд 9Ватиканский манускрипт (XI, Предложения, 31—33)
Классический труд Евклида, написанный в 3 веке
Слайд 10АКСИОМА – утверждение, не требующее доказательства.
Слово «аксиома» происходит от греческого «аксиос»,
Весь выбор аксиом (система) называется аксиоматикой
Слайд 11АКСИОМЫ ЕВКЛИДА
1. Равные одному и тому же равны и между собой.
2.
3. И если от равных отнимаются равные, то остатки будут равны.
4. И если к неравным прибавляются равные, то и целые не будут равны.
5. И удвоенные одного и того же равны между собой.
6. И половины одного и того же равны между собой.
7. И совмещающиеся друг с другом равны между собой.
8. И целое больше части.
9. И две прямые не содержат пространства.
Слайд 12ПОСТУЛАТ – утверждение не требующее доказательства (аксиомы и постулаты – не
Принципиальные различия:
В отличие от аксиомы (она имеет опытное происхождение) постулат может быть опровергнут опытом.
Если постулат может быть принят как произвольное предположительное утверждение, то аксиома – то, истинность чего очевидна
Слайд 13ПОСТУЛАТЫ ЕВКЛИДА
I. Требуется, чтобы от каждой
Слайд 14Пятый постулат Евклида
На современном языке:
Если сумма внутренних углов с
Слайд 15Пятый постулат Евклида
В школьных учебниках:
Через точку, не лежащую на
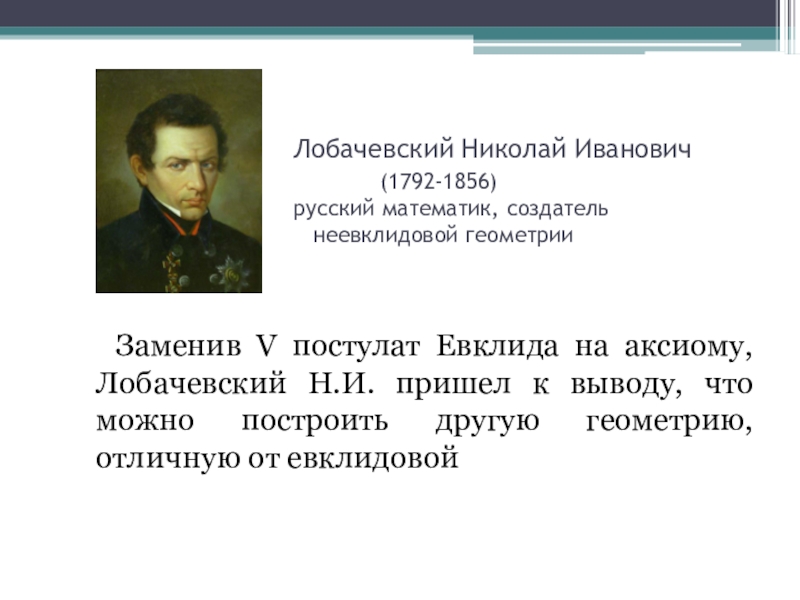
Слайд 16 Лобачевский
Заменив V постулат Евклида на аксиому, Лобачевский Н.И. пришел к выводу, что можно построить другую геометрию, отличную от евклидовой
Слайд 17«Чем отличается геометрия Лобачевского от геометрии Евклида?» Главное различие кроется в понимании
Слайд 18«Новая геометрия» Николая Лобачевского
Гиперболический параболоид
Воронка
Как показали исследования, геометрия Лобачевского (в
Слайд 19ВЫВОД
Несмотря на кажущиеся странности, геометрия Лобачевского является настоящей
Слайд 20Аксиомы планиметрии
Какова бы ни была прямая, существуют точки, принадлежащие этой прямой
Из трех точек на прямой одна о только одна лежит между двумя другими.
Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.
Каждый угол имеет определенную градусную меру, большую нуля. Градусная мера угла равна сумме градусных мер углов на которые он разбивается любым лучом, проходящим между его сторонами.
На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.
От полупрямой на содержащей её плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 0 , и только один.
Каков бы ни был треугольник, в этой же плоскости существует равный ему треугольник в заданном расположении относительно данной полупрямой в этой плоскости.
На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
Слайд 21Аксиомы стереометрии
Через любые три точки, не лежащие на одной прямой, проходит
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Слайд 22
Фридрих Бернхард Риман (1826-1866)
Немецкий математик,
Давид Гильберт
(1862-1942)
Немецкий математик, написал «Основания геометрии», в которых рассматриваются проблемы непротиворечивости, полноты и независимости систем аксиом, определяющих ту или иную геометрию
Слайд 23АКСИОМЫ В АЛГЕБРЕ
Свойства сложения
a+b=b+a
a+(b+c)=(a+b)+c
Свойства умножения
ab=ba
a(bc)=(ab)c
a(b+c)=ab+ac
Слайд 24АКСИОМЫ В ФИЗИКЕ
(1879-1955)
Немецкий физик-
теоретик
Ричард Фейнман
(1918-1988)
Американский
физик
Эйнштейн полагал, что вся его теория относительности базируется на двух аксиомах:
Принцип относительности может быть распространён на все явления нашего мира
Скорость света в вакууме – величина абсолютная, предельная для нашего мира.
Слайд 25ОСНОВНЫЕ АКСИОМЫ БИОЛОГИИ
Аксиома 1. Все живые организмы состоят из фенотипа и
Аксиома 2. Генетические программы не возникают заново, а реализуются матричным способом. В качестве матрицы, на которой строится ген будущего поколения, используется ген предыдущего поколения. Жизнь - это матричное копирование с последующей самосборкой копий (Н.К. Кольцов)
Аксиома 3. В процессе передачи из поколения в поколение генетические программы в результате многих причин изменяются случайно и не направленно, и лишь случайно эти изменения оказываются приспособительными. Отбор случайных изменений не только основа эволюции жизни, но и причина ее становления, потому что без мутаций отбор не действует. (Эта аксиома основана на принципах статистической физики и принципе неопределенности В. Гейзенберга)
Аксиома 4. В процессе формирования фенотипа случайные изменения генетических программ многократно усиливаются, что делает возможным их селекцию со стороны факторов внешней среды. Из-за усиления в фенотипах случайных изменений эволюция живой природы принципиально непредсказуема (Н.В. Тимофеев-Ресовский)
Слайд 26АКСИОМЫ В ФИЛОСОФИИ
Чтобы правильно построить философию, необходимо правильно начать философствовать, а
Такой аксиомой для Аристотеля является закон непротиворечия. Понятно, что для человека, который строит мост между бытиём и мышлением и ищет ответы на вопрос о сущности бытия в разуме, сложно было бы найти другой ответ.
Этот закон звучит следующим образом: «Невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении». Именно здесь мы видим ключ ко всей философии Аристотеля, то, что связывает воедино его философию, логику, этику, физику и все области знаний.
Слайд 27АКСИОМЫ В ГЕОГРАФИИ
Аксиома Григорьева А.А. о географической оболочке: географическая оболочка –
Положение о составе элементов системы географической оболочки. Природа элементов оболочки двойственна: с одной стороны, это любые объекты и явления природы, принадлежащие четырем геосферам; с другой – хорологические единицы природно-территориальных комплексов.
Положение о системе образующих отношениях. Обязательным атрибутом географической оболочки являются связи или отношения между ее элементами.
Положение о структуре географической оболочки. Структура географической оболочки порождается географическими элементами и взаимоотношениями между ними.
Аксиома об иерархии геосистем В.Б Сочавы. Географическая оболочка представляет собой систему, организованную в виде множества подсистем различных таксономических рангов.
Аксиома о границах геосистем В.С. Преображенского. Географическая оболочка как планетарная система обладает свойствами континуальности и дискретности, т.е. она непрерывно – дискретна по своему строению
Слайд 28АКСИОМЫ ЭКОЛОГИИ ЧЕЛОВЕКА
Аксиома экологии человека 1: эволюция и цивилизация
Аксиома экологии человека
Аксиома экологии человека 3: социализация и жизнеспособность
Аксиома экологии человека 4: роль совместной деятельности людей
Аксиома экологии человека 5: обмен информацией и развитие человечества
Аксиома экологии человека 6: взаимодействие человека и среды
Аксиома экологии человека 7: последствия взаимодействий человека и среды
Аксиома экологии человека 8: рост техногенных факторов риска
Аксиома экологии человека 9: двоякое влияние факторов среды на людей
Аксиома экологии человека 10: влияние факторов среды во времени
Аксиома экологии человека 11: экономическое развитие и здоровье
Аксиома экологии человека 12: ограничения роста населения Земли
Аксиома экологии человека 13: сотрудничество или глобальная катастрофа
Слайд 29 У каждого свой исходный постулат, на котором построена его
Н. Лобачевский
Слайд 32Аксиома жизни
Трикими
В нашей жизни аксиома,
Всё равно, что
Аксиома – дух сознанья,
Чудо миропониманья,
Ветер, Солнце, воды мира,
Слово, действия, стихира.
Жизнь и смерть в одном флаконе,
Пуля с порохом в патроне,
Шаг, что делит вновь и вновь,
Злую ненависть, любовь.
Бережливость и транжирство,
Преданность и дезертирство,
Безмятежность - жизни скупость,
Человеческую глупость.
Беспринципность в начинаньях,
Беспристрастность в обаяньях,
Вне сознания безбожность,
И без Бога осторожность...