№1 им. Н.Г. Чернышевского»
Руководитель : Рыгина Ирина Владимировна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к проекту Золотое сечение
Содержание
- 1. Презентация к проекту Золотое сечение
- 2. Иоганн Кеплер - немецкий астроном и математик
- 3. Цель проекта:Изучить математическую суть принципа «золотого сечения»
- 4. Гипотеза:Если ученые -математики античности и эпохи Возрождения
- 5. Оглавление: Введение.
- 6. Введение «Золотое сечение»
- 7. Математическая сущность золотого сечения.Пусть дан отрезок АВ,
- 8. Слайд 8
- 9. По теореме Пифагора ( АD +
- 10. Решим уравнение (2) относительно х:х² = а²
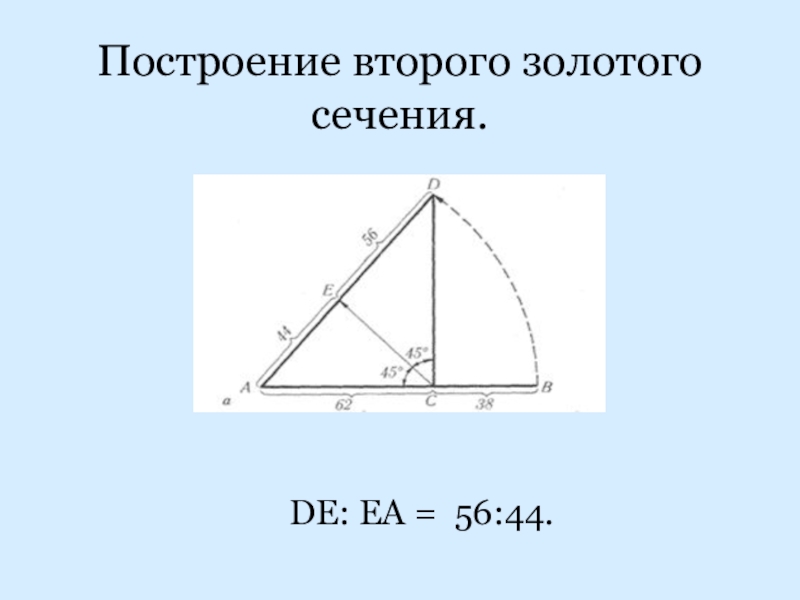
- 11. Построение второго золотого сечения. DЕ: ЕА = 56:44.
- 12. Связь золотой пропорции с рядом чисел последовательности
- 13. Показатель золотого сечения:Так, 21 : 34 ≈
- 14. . Применение золотого сечения в других науках.
- 15. Украшения из храма Тутанхамона.
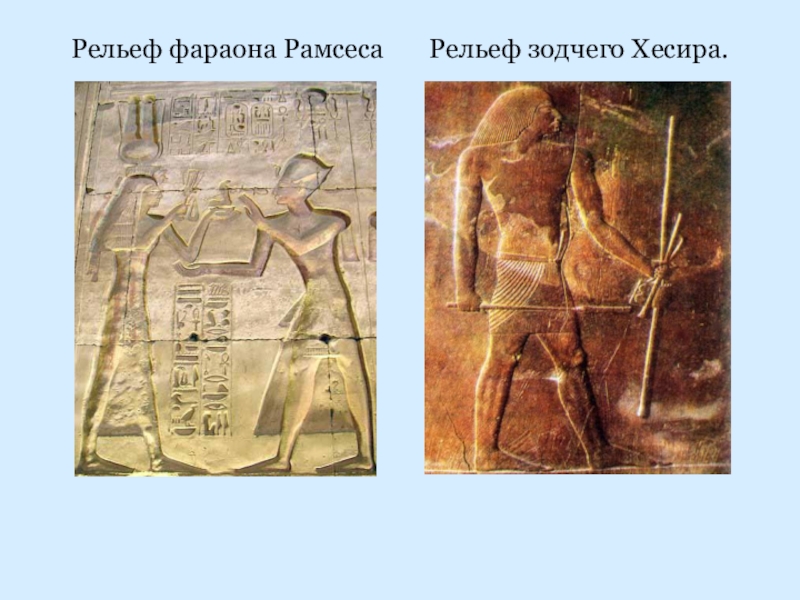
- 16. Рельеф фараона Рамсеса Рельеф зодчего Хесира.
- 17. Храм Парфенон и циркуль
- 18. Золотое сечение в наши дни. Дворец Мира и Согласия и Триумфальная арка
- 19. Семей –наш город.
- 20. Золотое сечение в природной среде.
- 21. Филотаксис
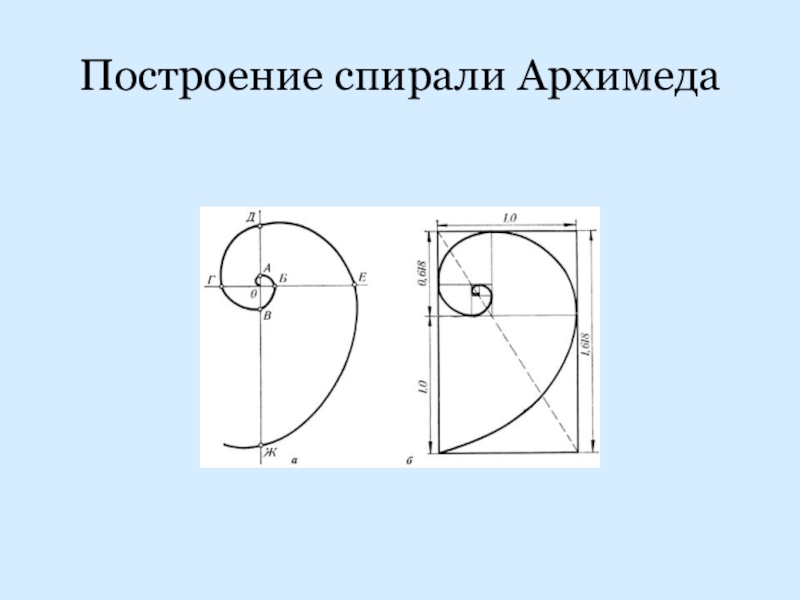
- 22. Построение спирали Архимеда
- 23. Измерение побегов Хлорофитума 10, 6,2 и 3,8см
- 24. Опыт Цейзинга В журнале «Наука
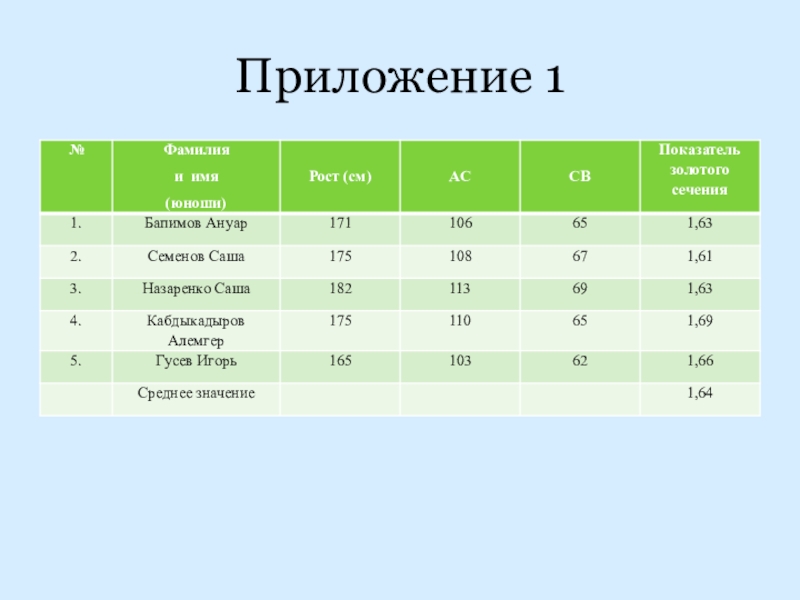
- 25. Приложение 1
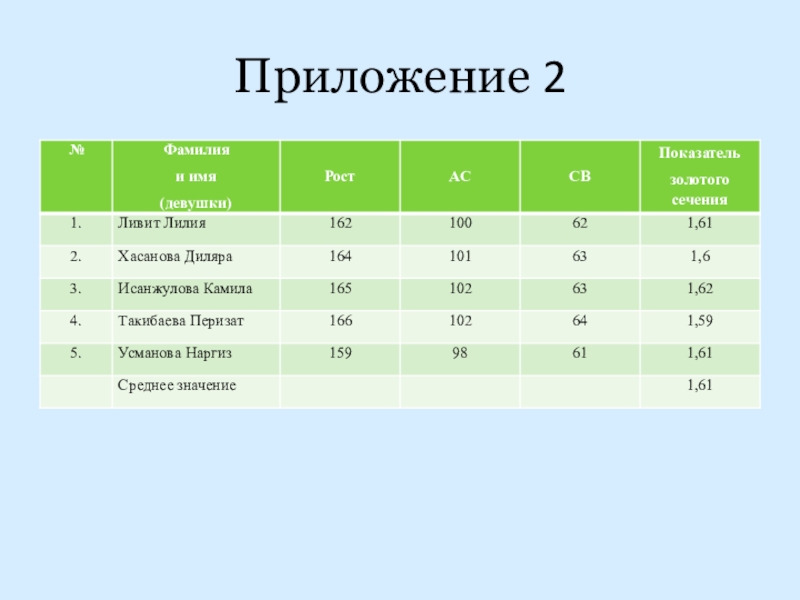
- 26. Приложение 2
- 27. Золотое сечение в живописи и фотографии
- 28. Вклад ученых в создание теории золотого сеченияПифагор
- 29. Спасибо За внимание
Иоганн Кеплер - немецкий астроном и математик «В геометрии существует два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем»1571-1630
Слайд 1Проект по математике
Золотое сечение
Авторы: Исанжулова Камила
Хасанова Диляра
учащиеся 10 «Б» класса
КГУ«СОШ
Слайд 2Иоганн Кеплер - немецкий астроном и математик
«В геометрии существует
два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем»
1571-1630
Слайд 3Цель проекта:
Изучить математическую суть принципа «золотого сечения» , исследовать историю вопроса,
а также рассмотреть применение в математике, архитектуре, живописи, фотографии , изучить литературу по данному вопросу, создать презентацию по золотому сечению.
Задача проекта - раскрыть метод «золотого сечения»,т.к в учебниках школьного курса математики материал по теме почти отсутствует
Задача проекта - раскрыть метод «золотого сечения»,т.к в учебниках школьного курса математики материал по теме почти отсутствует
Слайд 4Гипотеза:
Если ученые -математики античности и эпохи Возрождения использовали принцип «золотого сечения»
в математике, искусстве , музыке, архитектуре, то где в настоящее время применяются имеющиеся теоретические знания на практике. Найти формулы, поясняющие золотое сечение. Как золотое сечение применяется в геометрии? Как построить золотое сечение с помощью циркуля и линейки? Какими формулами пользуются при вычислении золотого сечения? Провести измерения на реальных объектах и убедиться в наличии золотой пропорции.
Слайд 5Оглавление:
Введение.
Глава 1. Золотое сечение в математике.
1.1 Математическая сущность золотого сечения.
1.2 Построение первого золотого сечения с помощью циркуля и линейки.
1.3 Построение второго золотого сечения.
1.4 Построение звездчатого пятиугольника, пентаграммы.
1.5 Связь золотой пропорции с рядом чисел последовательности Фибоначчи.
Глава 2. Применение «золотого сечения» в других науках.
2.1 Архитектурные объекты как источник наблюдения.
2.2 «Золотое сечение» в природной среде.
2.3 Использование золотого сечения в живописи и фотографии.
Заключение.
Список литературы.
Приложение ( таблицы №1, №2 )
Слайд 6Введение
«Золотое сечение» - это основной принцип
гармонии. В древности многие ученые изучали принцип «золотого сечения» и пришли к выводу, что его можно использовать прежде всего в математике при делении отрезка на две неравные части в среднем геометрическом отношении, а также в других науках, таких как: архитектура, живопись, поэзия. В настоящее время принцип «золотого сечения» используется в физике, биологии, статистике, в фотографии, в дизайне, в строительстве, при возведении архитектурных памятников и сооружений.
Слайд 7Математическая сущность золотого сечения.
Пусть дан отрезок АВ, отметим на нем точку
С таким образом, что АВ:АС=АС:СВ
Если при измерении отрезков выполняется пропорция, то точка С производит «золотое сечение» отрезка АВ.
Если при измерении отрезков выполняется пропорция, то точка С производит «золотое сечение» отрезка АВ.
А
С
В
х
а
а
а-х
Слайд 9
По теореме Пифагора
( АD + DC ) ² =
АВ² + ВC²
По построению имеем:
АD =АE, DC =ВC = 0,5 АВ.
Из этих равенств следует, что
АE² + АE · АВ = АВ²,
Отсюда получим равенство
По построению имеем:
АD =АE, DC =ВC = 0,5 АВ.
Из этих равенств следует, что
АE² + АE · АВ = АВ²,
Отсюда получим равенство
АВ : АС = АС : СВ
Слайд 10Решим уравнение (2) относительно х:
х² = а² - а х;
х² +
ах - а² =0;
D= а²- 4 · 1 · (-а)² = а² +4а² = 5а²;
х1/2 = (√5±1/2)а;
х1≈ 1,62 а; х2 ≈ 0,62а.
Не удов.
АЕ=62%; ВЕ=100%-62%=38%
Ответ: 62% и 38% части золотого сечения.
D= а²- 4 · 1 · (-а)² = а² +4а² = 5а²;
х1/2 = (√5±1/2)а;
х1≈ 1,62 а; х2 ≈ 0,62а.
Не удов.
АЕ=62%; ВЕ=100%-62%=38%
Ответ: 62% и 38% части золотого сечения.
Слайд 12Связь золотой пропорции с рядом чисел последовательности Фибоначчи.
1, 1, 2,
3, 5, 8, 13, 21, 34, 55, 89, 144,233,…
=
, где n-натуральное число.
8=3+5; 13=5+8; 21=8+13
Слайд 13Показатель золотого сечения:
Так, 21 : 34 ≈ 0,617, а 34 :
55 ≈ 0,618
Формула Бине ,связывающая числа Фибоначчи и Золотое сечение
Слайд 14. Применение золотого сечения в других науках.
Архитектурные объекты как источник наблюдений.
Статуи
–украшения храмов Пирамиды Хеопса в Египте
Слайд 24Опыт Цейзинга
В журнале «Наука и техника» описывается опыт
Цейзинга, который проводил измерения людей. Он заметил, что линия талии делит тело в отношении которое равняется в среднем 1,62. Точно также линия рта делит лицо человека, плечо, предплечье, кисти рук и пальцы также находятся в этом же отношении. Мы провели небольшой опыт по измерению своих одноклассников и заметили, что тела юношей находятся в отношении 13:8 и равняется числу 1,64, Для взрослых в норме 1,62. А тела девушек находятся в отношении 8:5 и равно 1,61. Для взрослых женщин среднее значение составляет 1,6. Для детей соотношение составляет 1:1, но к 15 годам приближается к золотому сечению взрослых.
Слайд 28Вклад ученых в создание теории золотого сечения
Пифагор
Стахов
Евклид Олсен
Платон Бендукидзе
Птолемей Лосев
Папп Эйнштейен
Гексикл Сороко
Лука Паччоли Волошин
Леонардо да Винчи Лаврус
Цейзинг
Евклид Олсен
Платон Бендукидзе
Птолемей Лосев
Папп Эйнштейен
Гексикл Сороко
Лука Паччоли Волошин
Леонардо да Винчи Лаврус
Цейзинг