год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к проекту: Золотое сечение
Содержание
- 1. Презентация к проекту: Золотое сечение
- 2. «Красота и гармония стали важнейшими категориями познания,
- 3. Формирование у учащихся понимания понятия золотого сечения;Формирование
- 4. Существование гармонии в окружающем нас мире. Применение знаний о золотом сечении в исследовании объектов города Ессентуки.ПРОБЛЕМА:
- 5. Подобрать литературу по теме «Золотое сечение»Провести исследования
- 6. В Древнем Египте существовала «система правил гармонии»,
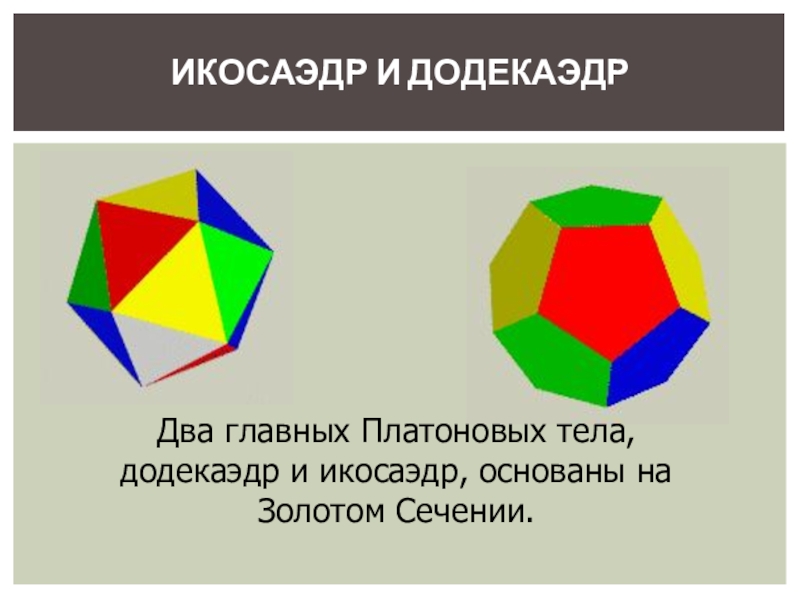
- 7. Два главных Платоновых тела, додекаэдр и икосаэдр, основаны на Золотом Сечении.ИКОСАЭДР И ДОДЕКАЭДР
- 8. С историей золотого сечения связано имя итальянского
- 9. Эпоха Возрождения ассоциируется с именами таких «титанов»,
- 10. Гениальный астроном Иоганн Кеплер (1571-1630) был последовательным
- 11. «Гармония – соразмерность частей и целого, слияние
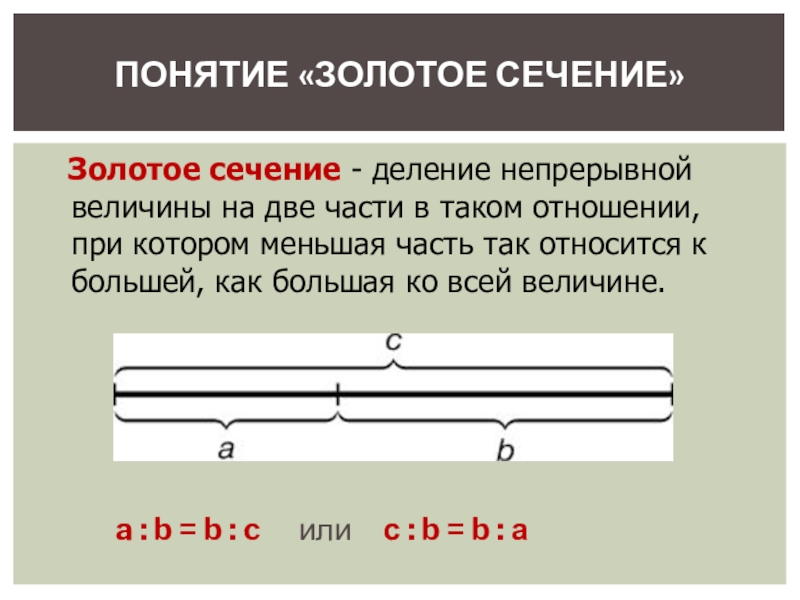
- 12. ПОНЯТИЕ «ЗОЛОТОЕ СЕЧЕНИЕ»a : b = b
- 13. Золотое сечение в процентах
- 14. Дано: отрезок АВ.Построить: золотое сечение отрезка АВ,
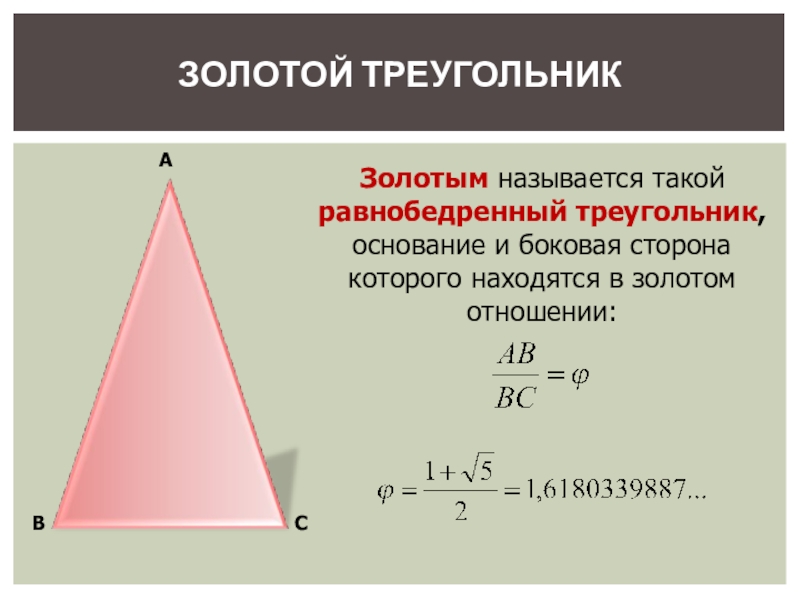
- 15. АВСЗолотым называется такой равнобедренный треугольник, основание и
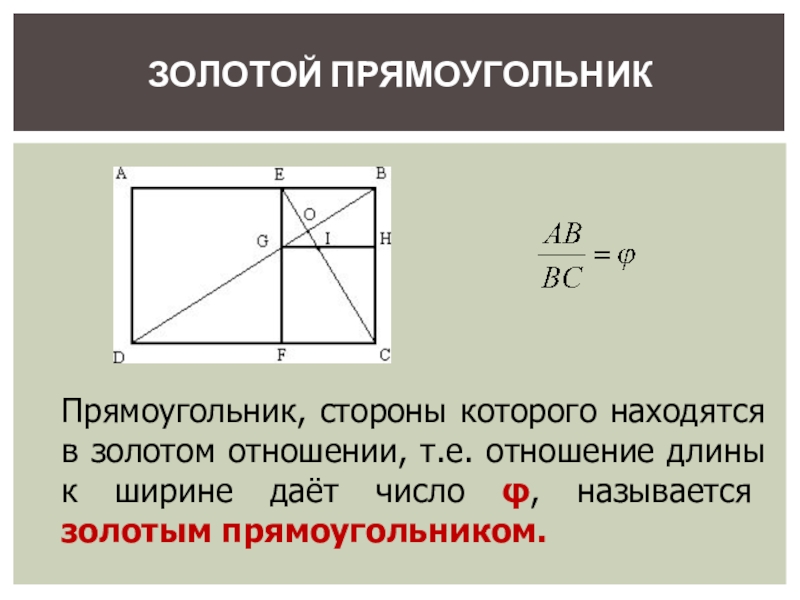
- 16. Прямоугольник, стороны которого находятся в золотом отношении,
- 17. ПЕНТАГРАММАЕсли в пентаграмме провести все диагонали, то
- 18. Последовательно отрезая от золотого прямоугольника квадраты и
- 19. Число ϕ является положительным корнем квадратного уравнения:x2
- 20. Все, что приобретало какую-то форму, образовывалось, росло,
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Цветки и семена подсолнуха, ромашки, чешуйки в
- 25. Золотая пропорция в теле ящерицы – длина
- 26. У многих бабочек узоры на крыльях, соотношение размеров грудной и брюшной части тела соответствуют золотой пропорции
- 27. РОГА И БИВНИ ЖИВОТНЫХ РАЗВИВАЮТСЯ В ФОРМЕ
- 28. В 1855 г. немецкий исследователь золотого сечения профессор
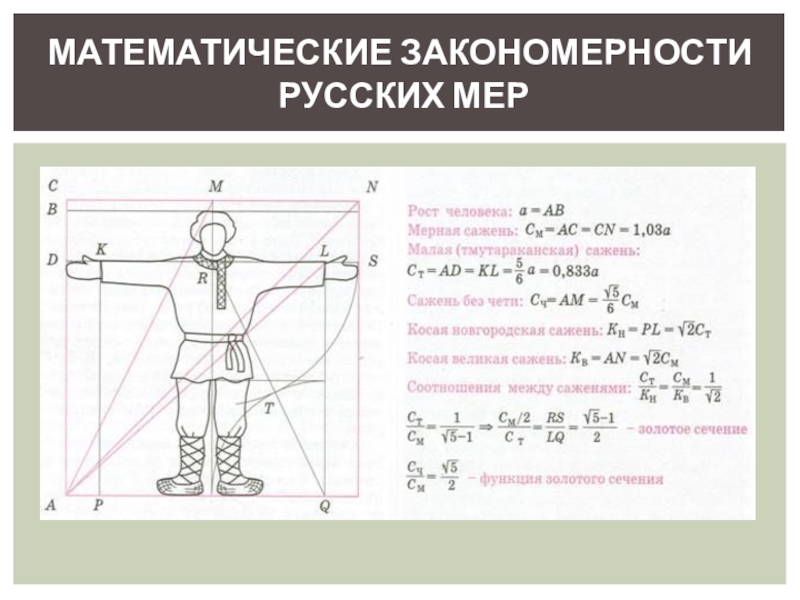
- 29. МАТЕМАТИЧЕСКИЕ ЗАКОНОМЕРНОСТИ РУССКИХ МЕР
- 30. ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ И ФОТОГРАФИИНа живописном
- 31. ЗОЛОТОЕ СЕЧЕНИЕ В СКУЛЬПТУРЕВенера МилосскаяДорифор Поликлета
- 32. ЗОЛОТОЕ СЕЧЕНИЕ В КАРТИНЕ ЛЕОНАРДО ДА
- 33. Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта
- 34. ЗОЛОТЫЕ ПРОПОРЦИИ ПАРФЕНОНА
- 35. Золотое соотношение мы можем увидеть и в здании Собора Парижской Богоматери
- 36. ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ РОССИИ Собор Христа Спасителя
- 37. Собор Василия Блаженного Храм Святителя Димитрия
- 38. Собор Вознесения Господня
- 39. Смольный соборПроект Смольного собора
- 40. Собор на Нерли
- 41. ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ ГОРОДА ЕССЕНТУКИ
- 42. ЗОЛОТЫЕ ПРОПОРЦИИ СВЯТО-ТРОИЦКОГО ХРАМА
- 43. ЗОЛОТЫЕ ПРОПОРЦИИ СВЯТО-ТРОИЦКОГО ХРАМА
- 44. Слайд 44
- 45. Понятие «золотое сечение» не изучается в школьном
«Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник ищет истину в красоте, а ученый – красоту в истине».
Слайд 1
Золотое сечение
Подготовили обучающиеся 9 класса
МБОУ ООШ №23
Руководитель:
Учитель математики Л. В. Абрамова
2017
Слайд 2«Красота и гармония стали важнейшими категориями познания, в определенной степени даже
его целью, ибо в конечном итоге художник ищет истину в красоте, а ученый – красоту в истине».
Стахов А.П.
Слайд 3Формирование у учащихся понимания понятия золотого сечения;
Формирование умений и навыков работы
с новым материалом;
Развитие эстетического и художественного вкуса, творческой активности и культуры обучающихся;
Формирование навыков группового общения, исследовательской и проектной деятельности.
Развитие эстетического и художественного вкуса, творческой активности и культуры обучающихся;
Формирование навыков группового общения, исследовательской и проектной деятельности.
ЦЕЛИ ПРОЕКТА:
Слайд 4Существование гармонии в окружающем нас мире.
Применение знаний о золотом сечении
в исследовании объектов города Ессентуки.
ПРОБЛЕМА:
Слайд 5Подобрать литературу по теме «Золотое сечение»
Провести исследования по следующим направлениям:
Ознакомиться с
историей золотого сечения
Дать формулировку понятия золотого сечения, рассмотреть алгебраический и геометрический смысл
Сформулировать понятие гармонии и математической гармонии
Исследовать пропорции тела человека по Цейзингу
Нахождение пропорции тела человека на примере обучающихся
Найти подтверждение наличия золотого сечения в природе
Рассмотреть применение золотого сечения в искусстве (скульптура, живопись, фотография)
Ознакомиться с применением золотого сечения в архитектуре
Исследования школьного двора
Анализ объектов архитектуры и скульптуры
Выводы по исследуемой теме
Дать формулировку понятия золотого сечения, рассмотреть алгебраический и геометрический смысл
Сформулировать понятие гармонии и математической гармонии
Исследовать пропорции тела человека по Цейзингу
Нахождение пропорции тела человека на примере обучающихся
Найти подтверждение наличия золотого сечения в природе
Рассмотреть применение золотого сечения в искусстве (скульптура, живопись, фотография)
Ознакомиться с применением золотого сечения в архитектуре
Исследования школьного двора
Анализ объектов архитектуры и скульптуры
Выводы по исследуемой теме
ЗАДАЧИ ПРОЕКТА:
Слайд 6В Древнем Египте существовала «система правил гармонии», основанная на Золотом Сечении.
В Древней Греции Золотое Сечение было своеобразным каноном культуры, который пронизывает все сферы науки и искусства. Красота и гармония стали важнейшими категориями познания.
В толковании древних греков понятие золотого сечения, и понятие гармонии идентичны.
Согласно Пифагору гармония имеет численное выражение, то есть, она связана с концепцией числа.
Евклид излагает теорию Платоновых тел, которая является существенным разделом геометрической теории Золотого Сечения.
ИСТОРИЯ «ЗОЛОТОГО СЕЧЕНИЯ»
Теория гармонии Древних
Слайд 7Два главных Платоновых тела, додекаэдр и икосаэдр, основаны на Золотом Сечении.
ИКОСАЭДР
И ДОДЕКАЭДР
Слайд 8
С историей золотого сечения связано имя итальянского математика Леонардо Фибоначчи.
Ряд
чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи.
Каждый член последовательности, начиная с третьего, равен сумме двух предыдущих, а отношение смежных чисел ряда приближается к отношению золотого деления.
Все исследователи золотого деления в растительном и в животном мире, искусстве, неизменно приходили к ряду Фибоначчи как арифметическому выражению закона золотого деления.
Каждый член последовательности, начиная с третьего, равен сумме двух предыдущих, а отношение смежных чисел ряда приближается к отношению золотого деления.
Все исследователи золотого деления в растительном и в животном мире, искусстве, неизменно приходили к ряду Фибоначчи как арифметическому выражению закона золотого деления.
РЯД ФИБОНАЧЧИ
Слайд 9Эпоха Возрождения ассоциируется с именами таких «титанов», как Леонардо да Винчи,
Микеланджело, Рафаэль, Николай Коперник, Альберт Дюрер, Лука Пачоли.
Имеется много авторитетных свидетельств о том, что именно Леонардо да Винчи(1452-1519) был одним из первых, кто ввел сам термин «Золотое Сечение».
«Витрувийский человек» - размах вытянутых в сторону рук человека примерно равен его росту, вследствие чего фигура человека вписывается в квадрат и в круг.
Рисунок и текст иногда называют каноническими пропорциями.
Имеется много авторитетных свидетельств о том, что именно Леонардо да Винчи(1452-1519) был одним из первых, кто ввел сам термин «Золотое Сечение».
«Витрувийский человек» - размах вытянутых в сторону рук человека примерно равен его росту, вследствие чего фигура человека вписывается в квадрат и в круг.
Рисунок и текст иногда называют каноническими пропорциями.
«ЗОЛОТАЯ ПРОПОРЦИЯ» - ГЛАВНЫЙ ЭСТЕТИЧЕСКИЙ ПРИНЦИП ЭПОХИ СРЕДНЕВЕКОВЬЯ
Слайд 10Гениальный астроном Иоганн Кеплер (1571-1630) был последовательным приверженцем Золотого Сечения, Платоновых
тел и Пифагорейской доктрины о числовой гармонии Мироздания.
Считается, что именно Кеплер обратил внимание на ботаническую закономерность филлотаксиса и установил связь между числами Фибоначчи и золотой пропорцией, доказав, что последовательность отношений соседних чисел Фибоначчи:
1/1; 2/1; 3/2; 5/3 ;8/5; 13/8;…в пределе стремится к золотой пропорции
Считается, что именно Кеплер обратил внимание на ботаническую закономерность филлотаксиса и установил связь между числами Фибоначчи и золотой пропорцией, доказав, что последовательность отношений соседних чисел Фибоначчи:
1/1; 2/1; 3/2; 5/3 ;8/5; 13/8;…в пределе стремится к золотой пропорции
ВКЛАД КЕПЛЕРА
В ТЕОРИЮ ЗОЛОТОГО СЕЧЕНИЯ
Слайд 11«Гармония – соразмерность частей и целого, слияние различных компонентов объекта в
единое органическое целое. В гармонии получают внешнее выявление внутренняя упорядоченность и мера бытия» -Большая Советская Энциклопедия
Математическая гармония - это равенство или соразмерность частей с друг другом и части с целым.
Понятие математической гармонии тесно связано с понятиями пропорции и симметрии.
Математическая гармония - это равенство или соразмерность частей с друг другом и части с целым.
Понятие математической гармонии тесно связано с понятиями пропорции и симметрии.
МАТЕМАТИЧЕСКОЕ ПОНИМАНИЕ
ГАРМОНИИ
Слайд 12ПОНЯТИЕ «ЗОЛОТОЕ СЕЧЕНИЕ»
a : b = b : c
или с : b = b : а
Золотое сечение - деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
Слайд 14Дано: отрезок АВ.
Построить: золотое сечение отрезка АВ, т.е. точку Е так,
чтобы .
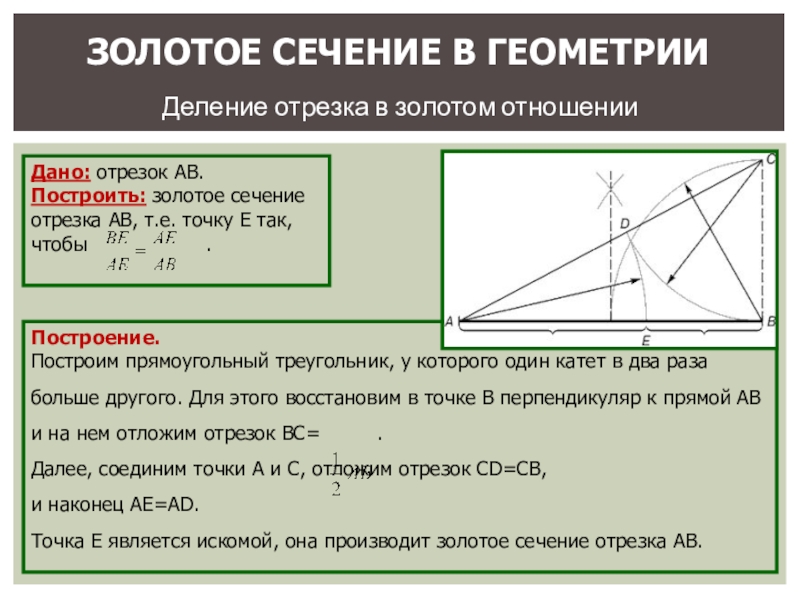
Построение.
Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок ВС= .
Далее, соединим точки А и С, отложим отрезок CD=CB,
и наконец AE=AD.
Точка Е является искомой, она производит золотое сечение отрезка АВ.
Деление отрезка в золотом отношении
ЗОЛОТОЕ СЕЧЕНИЕ В ГЕОМЕТРИИ
Слайд 15А
В
С
Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся
в золотом отношении:
ЗОЛОТОЙ ТРЕУГОЛЬНИК
Слайд 16Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение длины к
ширине даёт число φ, называется золотым прямоугольником.
ЗОЛОТОЙ ПРЯМОУГОЛЬНИК
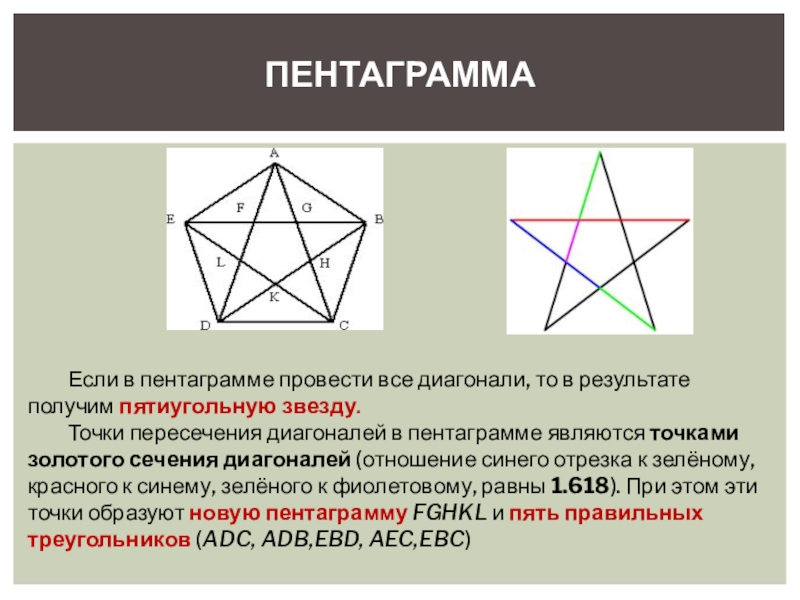
Слайд 17ПЕНТАГРАММА
Если в пентаграмме провести все диагонали, то в результате получим пятиугольную
звезду.
Точки пересечения диагоналей в пентаграмме являются точками золотого сечения диагоналей (отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому, равны 1.618). При этом эти точки образуют новую пентаграмму FGHKL и пять правильных треугольников (ADC, ADB,EBD, AEC,EBC)
Точки пересечения диагоналей в пентаграмме являются точками золотого сечения диагоналей (отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому, равны 1.618). При этом эти точки образуют новую пентаграмму FGHKL и пять правильных треугольников (ADC, ADB,EBD, AEC,EBC)
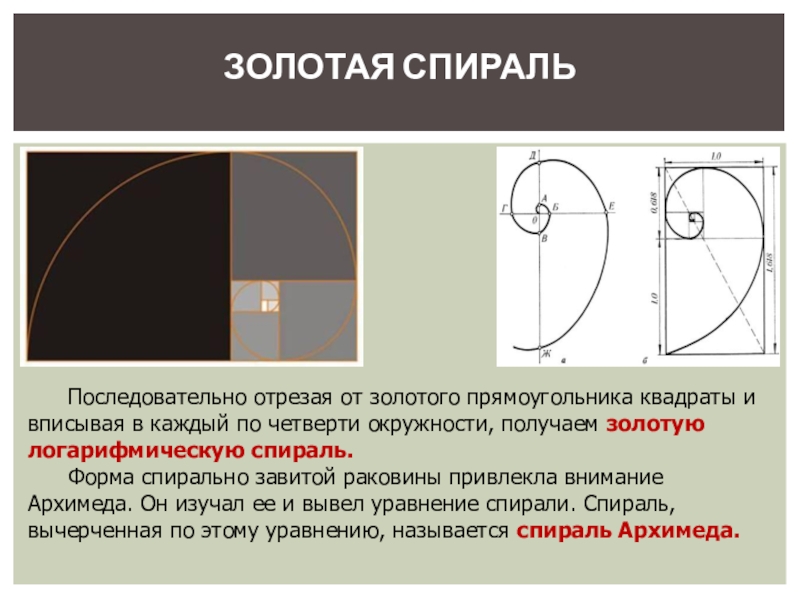
Слайд 18Последовательно отрезая от золотого прямоугольника квадраты и вписывая в каждый по
четверти окружности, получаем золотую логарифмическую спираль.
Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется спираль Архимеда.
Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется спираль Архимеда.
ЗОЛОТАЯ СПИРАЛЬ
Слайд 19Число ϕ является положительным корнем квадратного уравнения:
x2 = x + 1
подставим корень ϕ вместо x и разделим на ϕ :
Если продолжить такую подстановку бесконечное число раз, то получим цепную дробь:
Аналогично, если взять корень квадратный из правой и левой частей первого тождества, то получим представление золотой пропорции в «радикалах»:
«ЗОЛОТОЕ СЕЧЕНИЕ» - ГАРМОНИЯ МАТЕМАТИКИ
Слайд 20 Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в
пространстве и сохранить себя.
Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.
Гете называл спираль "кривой жизни". Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Паук плетет паутину спиралеобразно.
Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.
Гете называл спираль "кривой жизни". Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Паук плетет паутину спиралеобразно.
ЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕ
Слайд 24Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках
"упакованы" по логарифмическим ("золотым") спиралям, завивающимся навстречу друг другу, причем числа "правых "и "левых" спиралей всегда относятся друг к другу, как соседние числа Фибоначчи.
Слайд 25 Золотая пропорция в теле ящерицы – длина хвоста так относится к
длине остального тела, как 62 к 38
Слайд 26 У многих бабочек узоры на крыльях, соотношение размеров грудной и брюшной
части тела соответствуют золотой пропорции
Слайд 27 РОГА И БИВНИ ЖИВОТНЫХ РАЗВИВАЮТСЯ В ФОРМЕ СПИРАЛИ. БИВНИ СЛОНОВ И
ВЫМЕРШИХ МАМОНТОВ, КОГТИ ЛЬВОВ И КЛЮВЫ ПОПУГАЕВ ЯВЛЯЮТ СОБОЙ ЛОГАРИФМИЧЕСКИЕ ФОРМЫ И НАПОМИНАЮТ ФОРМУ ОСИ, СКЛОННОЙ ОБРАТИТЬСЯ В СПИРАЛЬ.
Слайд 28В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд
«Эстетические исследования». Он измерил около двух тысяч человеческих тел и пришел к выводу, что пропорции золотого сечения проявляются в отношении частей тела человека – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Деление тела точкой пупа – важнейший показатель золотого сечения.
Деление тела точкой пупа – важнейший показатель золотого сечения.
МАТЕМАТИЧЕСКАЯ ЭСТЕТИКА
ЦЕЙЗИНГА
Слайд 30ЗОЛОТОЕ СЕЧЕНИЕ В ЖИВОПИСИ И ФОТОГРАФИИ
На живописном полотне существуют четыре точки
повышенного внимания.
Зрительные центры расположены на расстоянии 3/8 и 5/8 от краев любой картины и фотографии.
Зрительные центры расположены на расстоянии 3/8 и 5/8 от краев любой картины и фотографии.
Слайд 32ЗОЛОТОЕ СЕЧЕНИЕ В КАРТИНЕ
ЛЕОНАРДО ДА ВИНЧИ "ДЖОКОНДА"
Портрет Моны Лизы привлекает
тем, что композиция рисунка построена на"золотых треугольниках" (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника).
Слайд 33Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы
Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
ЗОЛОТОЕ СЕЧЕНИЕ В АРХИТЕКТУРЕ
Пирамида Хеопса
Слайд 45Понятие «золотое сечение» не изучается в школьном курсе математики, а рассматривается
как гуманитарный фон в историческом развитии математики.
В данной работе рассмотрены способы нахождения «Золотого сечения», изложены примеры золотой пропорции в природе и теле человека, в архитектуре зданий города Ессентуки, в расположении зрительных центров на фотографиях.
В архитектуре пропорции совпадают с коэффициентом золотого сечения.
Многое в окружающей нас природе подчиняется правилу золотого сечения.
В данной работе рассмотрены способы нахождения «Золотого сечения», изложены примеры золотой пропорции в природе и теле человека, в архитектуре зданий города Ессентуки, в расположении зрительных центров на фотографиях.
В архитектуре пропорции совпадают с коэффициентом золотого сечения.
Многое в окружающей нас природе подчиняется правилу золотого сечения.
ВЫВОДЫ
