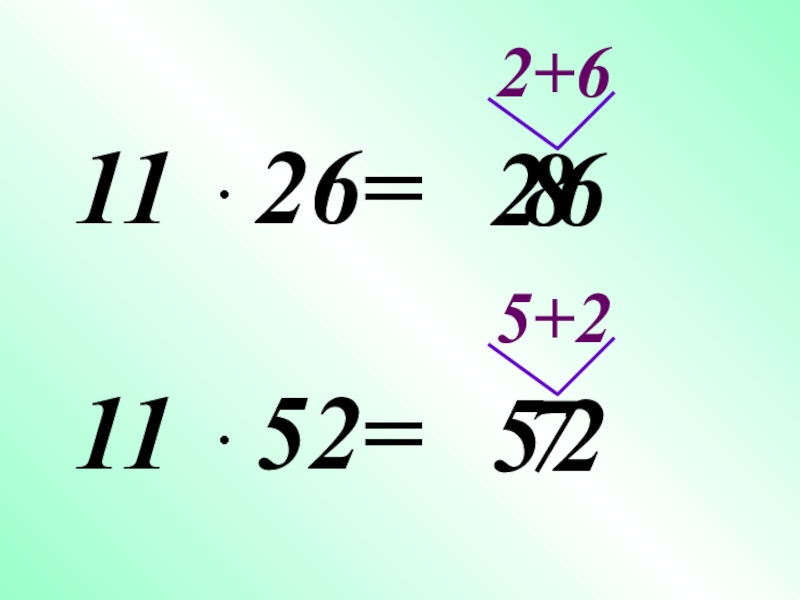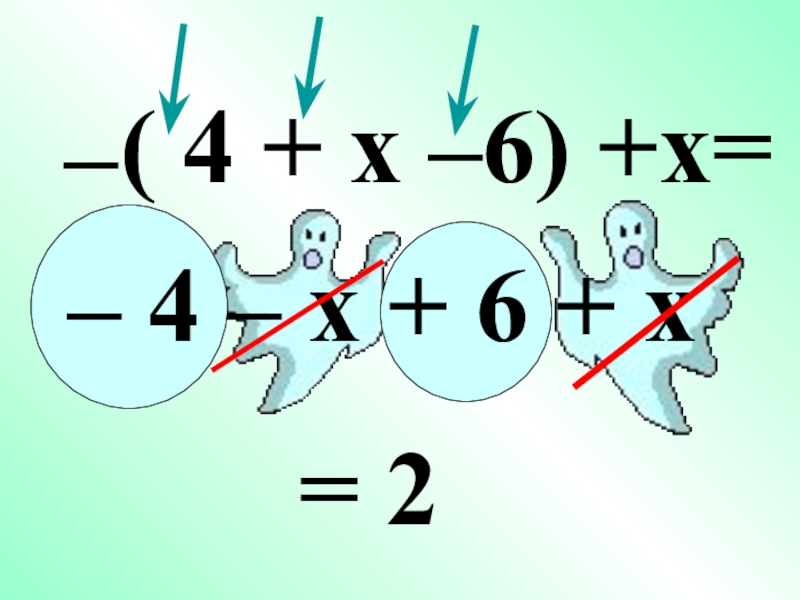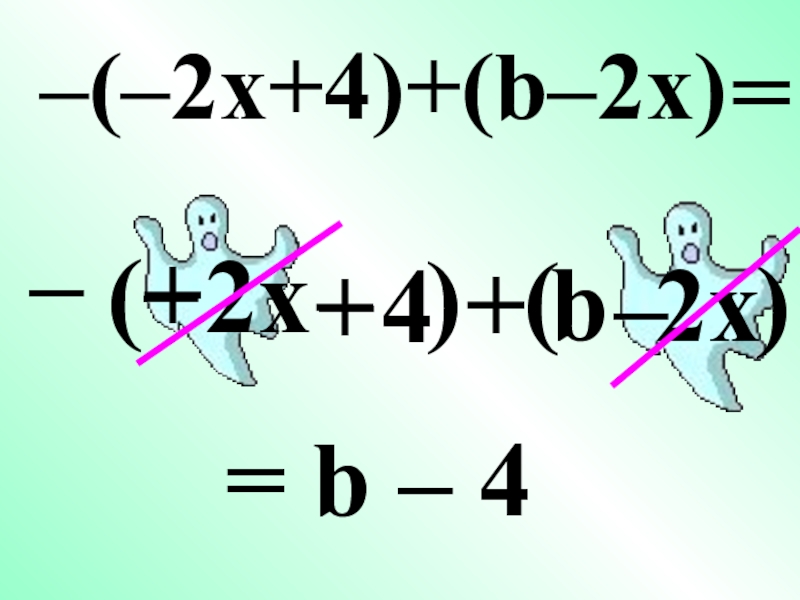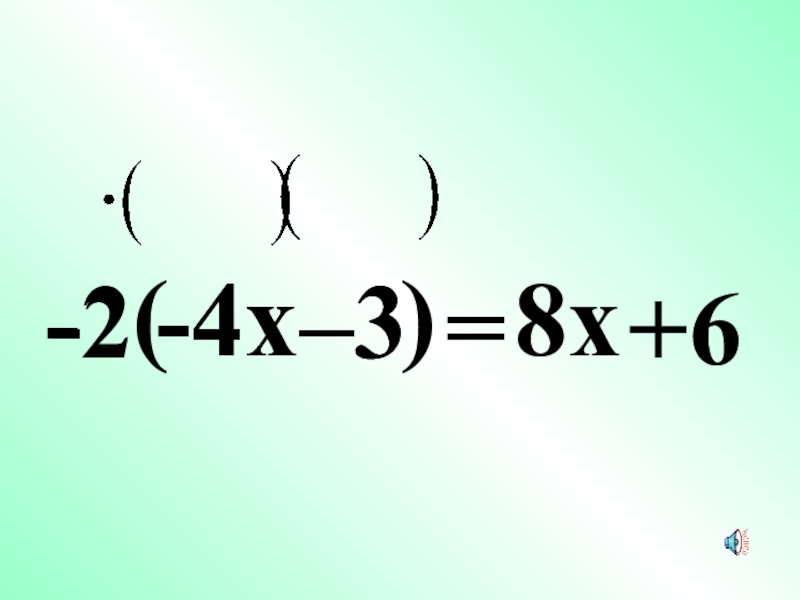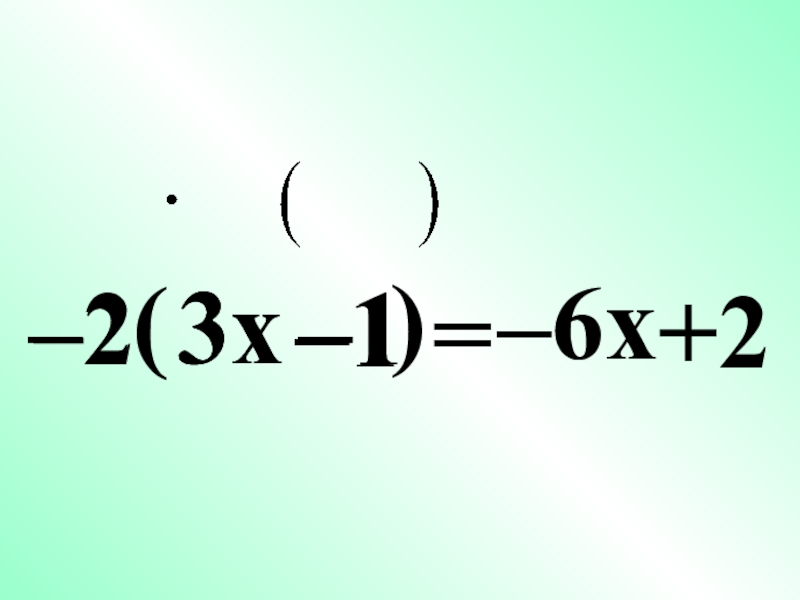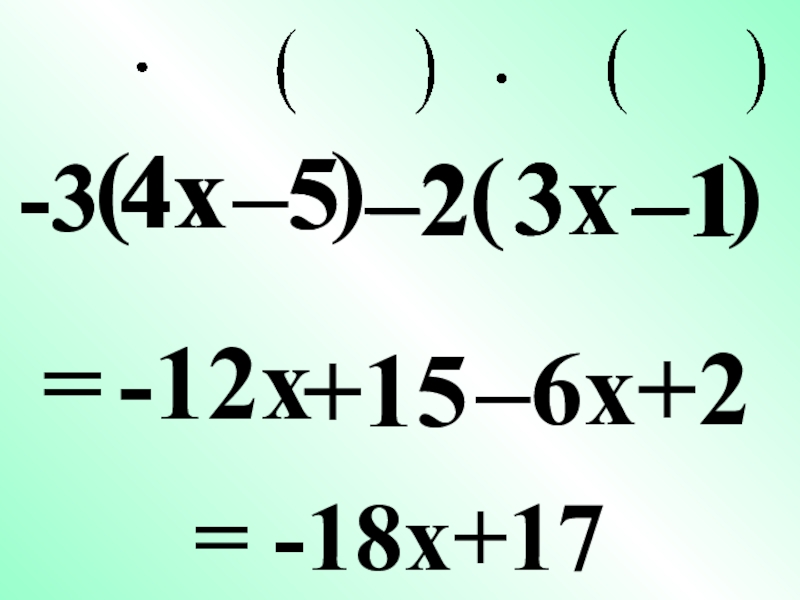- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к открытому уроку по теме: Раскрытие скобок 6 класс.
Содержание
- 1. Презентация к открытому уроку по теме: Раскрытие скобок 6 класс.
- 2. Название произошло от введенного Эйлером немецкого термина
- 3. cМы знаем!Распределительный закон умножения.a(b)=ab+acab+ cРаскрытие скобок
- 4. baaМы знаем!Распределительный закон умножения.=+acВынесение за скобкиобщего множителяacb
- 5. + cРаспределительный закон умножения.a(b)=ab+acРаскрытие скобокВынесение за скобкиобщего множителя
- 6. Применение распределительного закона умножения для быстрого счета.
- 7. 268527
- 8. Применение распределительного закона умножения для быстрого счета.
- 9. Применение распределительного закона умножения для быстрого счета.
- 10. Гимнастика для глаз
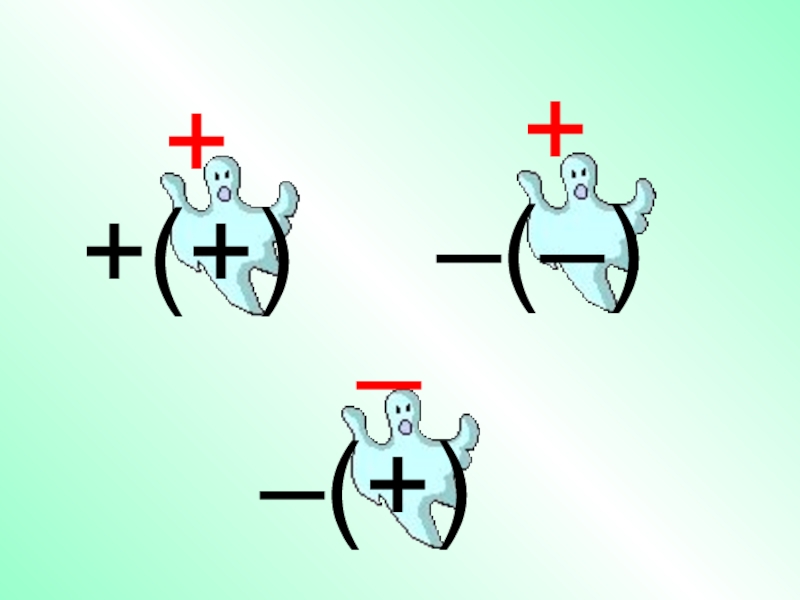
- 11. –(–)–(+)–++(+)+
- 12. +(+(–3x+2b–m)=–3x+2b–m)Если перед скобками стоит знак «+»,то при раскрытии скобок знаки слагаемых в скобках сохраняются.
- 13. +(+(x–2n–k)=x–2n–k)Если перед скобками стоит знак «+»,то при раскрытии скобок знаки слагаемых в скобках сохраняются.
- 14. –(–2x+4+b–k)–(–2x+4+b–k)+––+=Если перед скобками стоит знак «–»,то при раскрытии скобок знаки слагаемых в скобках заменяются на противоположные.
- 15. –Если перед скобками стоит знак «–»,то при
- 16. ( 4 + x –6) +x=–– 4 – x + 6 + x= 2
- 17. –(–2x+4+b2x)–(–2x+4)+(b–2x)+––=()= b – 4
- 18. –(a+b)= –a–b+a+bРаскрой скобки. Щелкни мышкой по выражениям,
- 19. –5-3-3–5(4x)=-12x+154xДля раскрытия скобок используем распределительный закон умножения.
- 20. -2–3-2–3(-4x)=8x+6-4x
- 21. –2(3x–1)=–6x+2–2–13x
- 22. –5–2(3x–1)=–6x+2–2–13x-3-3–5(4x)4x-12x+15= -18x+17
Название произошло от введенного Эйлером немецкого термина Klammer – «скобки». До появления специальных символов перед выражением, которое нужно заключить в скобки, ставилось слово Collect или буквы сs от communis, u от universal или b, означающее binomial,
Слайд 2Название произошло от введенного Эйлером
немецкого термина Klammer – «скобки».
До
появления специальных символов перед
выражением, которое нужно заключить в скобки,
ставилось слово Collect или буквы сs от communis,
u от universal или b, означающее binomial, и др.
выражением, которое нужно заключить в скобки,
ставилось слово Collect или буквы сs от communis,
u от universal или b, означающее binomial, и др.
Экскурс в историю математических символов
Фигурные скобки появляются в сочинениях Виета (1593)
Широкое применение скобки получили лишь в первой половине XVIII века, благодаря Лейбницу и еще больше Эйлеру.
Слайд 5+ c
Распределительный закон умножения.
a
(
b
)
=
ab
+ac
Раскрытие скобок
Вынесение за скобки
общего множителя
Слайд 12+
(
+(–3x+2b–m)=
–3x+2b–m
)
Если перед скобками стоит знак «+»,
то при раскрытии скобок знаки
слагаемых
в скобках сохраняются.
Слайд 13+
(
+(x–2n–k)=
x–2n–k
)
Если перед скобками стоит знак «+»,
то при раскрытии скобок знаки
слагаемых
в скобках сохраняются.
Слайд 14–
(
–
2x
+
4
+
b
–
k
)
–(–2x+4+b–k)
+
–
–
+
=
Если перед скобками стоит знак «–»,
то при раскрытии скобок знаки
слагаемых
в скобках заменяются
на противоположные.
на противоположные.
Слайд 15–
Если перед скобками стоит знак «–»,
то при раскрытии скобок знаки
слагаемых
в скобках заменяются
на противоположные.
на противоположные.
–
(
+
2x
+
3f
–
m
–
h
)
–( 2x+3f–m–h)
–
+
+
=
+
Слайд 18
–(a+b)=
–a
–b
+a
+b
Раскрой скобки. Щелкни мышкой по выражениям, которые считаешь
правильными. Не
ошибайся, твои ошибки все увидят!
–(a–b)=
–a
+b
+a
–b
–(–х+у)=
–у
+х
+у
–х
d–(–k+t)=
d
+k
+t
–k
–t
–m+(a – c)=
–c
+a
+c
–a
–m
p –(–n+ r –s)=
p
+n
+r
–n
–r
–(k+t)+(–a–s)=
–a
–k
+k
+s
–t
–(d–x)–(y–z)=
+x
–y
+d
+y
+z
–s
+s
–s
+a
+t
–x
–d
–z
