- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к открытому уроку
Содержание
- 1. Презентация к открытому уроку
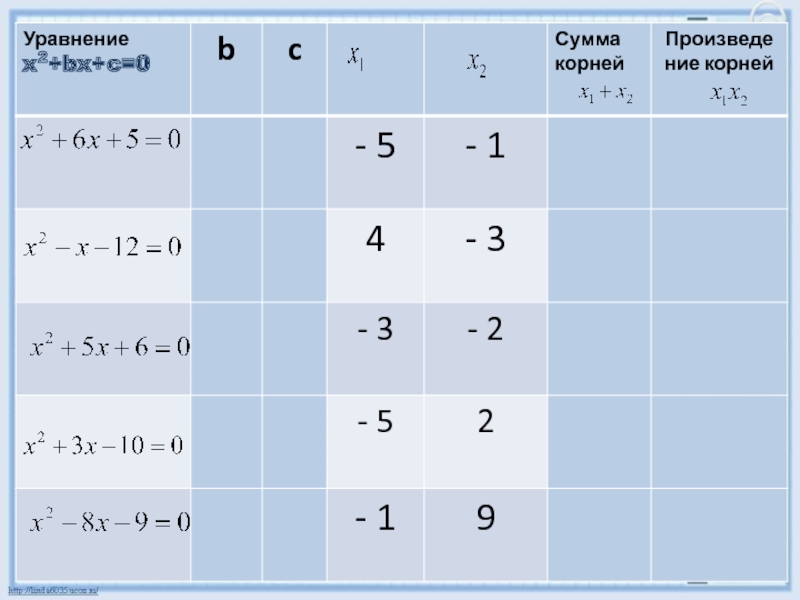
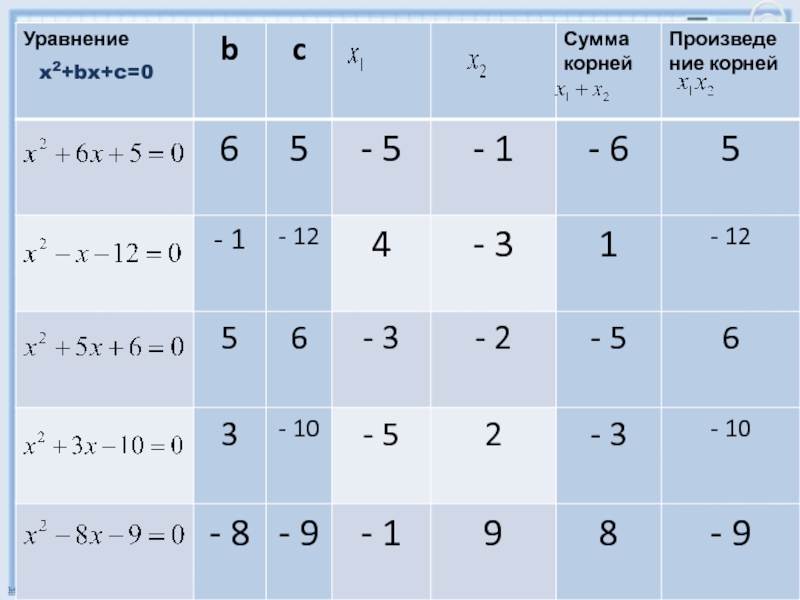
- 2. а) х2-13х+30=0б) 2х2+3х+1=0в) х2-26х+120=0 г) 3х2-7х+3=0д)3х2+16х+8=0 Выберите приведенные уравнения и найдите корни
- 3. Найдите сумму и произведение корней квадратного уравненияХ2-25х+100=05х2+13х+1=0Х2-8х+12=0 3х2-17х+3=03Х2+16х+8=0
- 4. 3 10 6
- 5. Слайд 5
- 6. Тема урока Теорема Виета
- 7. Слайд 7
- 8. x2+bx+c=0
- 9. Заполните пропускиСумма корней --------------квадратного уравнения
- 10. Если числа х1 и х2
- 11. • Какие уравнения мы сегодня рассматривали?• Чему
- 12. Задание на дом1. Знать формулировки теоремы Виета
- 13. Самостоятельная работа.Х2+ 6х + 8 = 0Х2
- 14. Проверьте себя:x2+ 6х + 8 = 0
- 15. Алгоритм нахождения корней: 1)Определить знаки корней уравнения.2)Подобрать
а) х2-13х+30=0б) 2х2+3х+1=0в) х2-26х+120=0 г) 3х2-7х+3=0д)3х2+16х+8=0 Выберите приведенные уравнения и найдите корни
Слайд 2а) х2-13х+30=0
б) 2х2+3х+1=0
в) х2-26х+120=0
г) 3х2-7х+3=0
д)3х2+16х+8=0
Выберите приведенные уравнения и найдите
корни
Слайд 3Найдите сумму и произведение корней квадратного уравнения
Х2-25х+100=0
5х2+13х+1=0
Х2-8х+12=0
3х2-17х+3=0
3Х2+16х+8=0
Слайд 5 Франсуа́ Вие́т
(1540 — 13
февраля 1603)
Родился во Франции, был адвокатом и советником королей Генриха III и IV. Будучи выдающимся математиком, сумел раскрыть ключ шифра, состоявшего из 500 знаков, с помощью которого враги короля вели переписку с испанским двором. Был приговорён испанской инквизицией к сожжению на костре. Среди математиков известен своей теоремой о свойствах корней квадратного уравнения, обнародованной в 1591 году.
Родился во Франции, был адвокатом и советником королей Генриха III и IV. Будучи выдающимся математиком, сумел раскрыть ключ шифра, состоявшего из 500 знаков, с помощью которого враги короля вели переписку с испанским двором. Был приговорён испанской инквизицией к сожжению на костре. Среди математиков известен своей теоремой о свойствах корней квадратного уравнения, обнародованной в 1591 году.
Слайд 9Заполните пропуски
Сумма корней --------------
квадратного уравнения равна второму коэффициенту,
-----------------------------------------------,
а
–------------------------
корней равно свободному члену.
корней равно свободному члену.
приведенного
взятому с противоположным знаком
произведение
Слайд 10Если числа х1 и х2
являются корнями
уравнения
х2+bх+c=0,
то справедливы формулы
х1+х2=-b х1∙х2=c
т.е.сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
х2+bх+c=0,
то справедливы формулы
х1+х2=-b х1∙х2=c
т.е.сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Теорема Виета.
Слайд 11• Какие уравнения мы сегодня рассматривали?
• Чему равна сумма корней квадратного
уравнения?
• Чему равно произведение корней квадратного уравнения?
Продолжите фразы:
• Сегодня на уроке я узнал...
• Сегодня на уроке я научился...
• Сегодня на уроке я познакомился...
• Чему равно произведение корней квадратного уравнения?
Продолжите фразы:
• Сегодня на уроке я узнал...
• Сегодня на уроке я научился...
• Сегодня на уроке я познакомился...
Подведём итог!
Слайд 12Задание на дом
1. Знать формулировки теоремы Виета и теоремы, обратной теореме
Виета.
2. Закончить доказательство теоремы Виета:
3. Учебник §21, №710,712
Слайд 13Самостоятельная работа.
Х2+ 6х + 8 = 0
Х2 + х - 90
= 0
Х2 - 10х - 24 = 0
Х2 - 15х + 14 = 0
-Х2+ 7х + 8 = 0
Х2 - 10х - 24 = 0
Х2 - 15х + 14 = 0
-Х2+ 7х + 8 = 0
Слайд 14Проверьте себя:
x2+ 6х + 8 = 0
x1=-2; x2 =-4
Х2 + х - 90 = 0 x1=-10; x2 =9
Х2- 10х -24=0 x1=12; x2 =-2
Х2- 15х +14=0 x1=14; x2 =1
-Х2+ 7х + 8 = 0 •(-1)
Х2 + х - 90 = 0 x1=-10; x2 =9
Х2- 10х -24=0 x1=12; x2 =-2
Х2- 15х +14=0 x1=14; x2 =1
-Х2+ 7х + 8 = 0 •(-1)
Слайд 15Алгоритм нахождения корней:
1)Определить знаки корней уравнения.
2)Подобрать пары целых чисел, произведение которых
равно q.
3)Из найденных пар чисел выбрать ту пару, которая в сумме будет равна –p.
4)Записать ответ.
3)Из найденных пар чисел выбрать ту пару, которая в сумме будет равна –p.
4)Записать ответ.