комбинаторике
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к интегрированным урокам по теории вероятностей и информатике на тему Перебор различных вариантов. Правило умножения. Презентации. (6 класс)
Содержание
- 1. Презентация к интегрированным урокам по теории вероятностей и информатике на тему Перебор различных вариантов. Правило умножения. Презентации. (6 класс)
- 2. Как говорят о событиях, которые в
- 3. Какое это событие?Черепаха научится говоритьневозможное Вода
- 4. Тестирование
- 5. _______________________________________________________________
- 6. №1. Выберите верное предложение I вариант
- 7. № 2. Выберите достоверное событие
- 8. № 3. Выберите невозможное событие из предложенных
- 9. № 4. Выберите случайное событие из
- 10. № 5. Вставьте нужное слово в определение
- 11. Слайд 11
- 12. Объяснение нового материала
- 13. Малыш, гуляя, случайным образом перебирает различные варианты
- 14. КОМБИНАТОРИКА – это раздел математики, посвященный решению
- 15. Блез Паскаль(1623-1662)Пьер Ферма(1601-1665)Якоб Бернули(1654-1705) Готфрид Лейбниц(1646-1716)
- 16. Задача 1Туристическая фирма планирует посещение туристами в
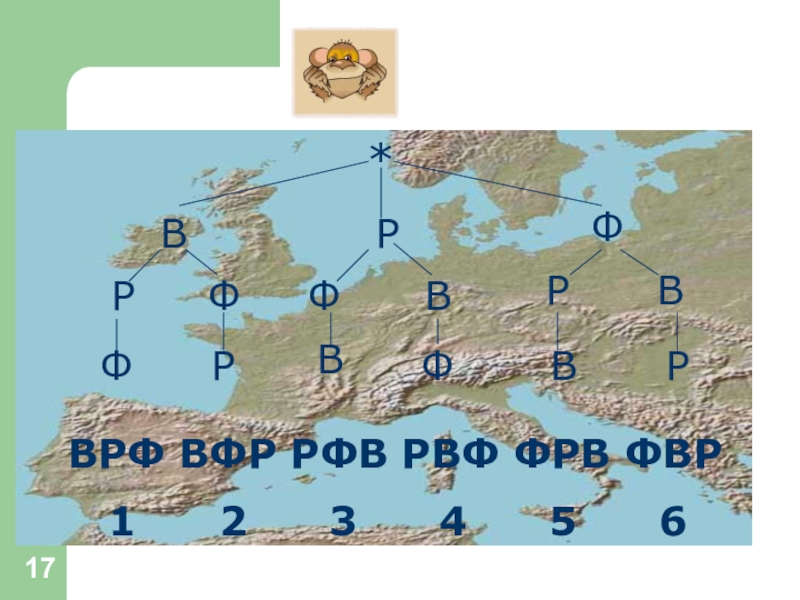
- 17. *ВРФ ВФР РФВ РВФ ФРВ ФВР
- 18. Задача 2.От турбазы к горному озеру ведут
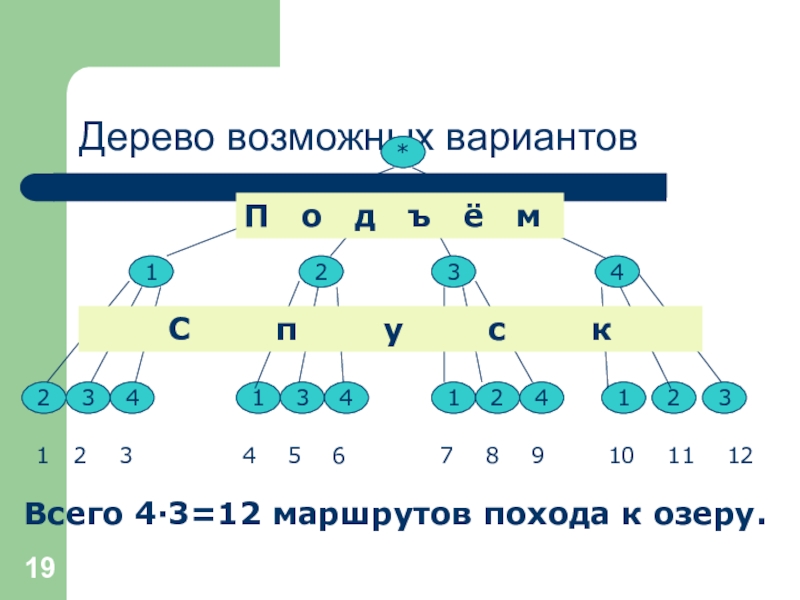
- 19. Дерево возможных вариантов**1234234134124123Всего 4∙3=12 маршрутов похода к
- 20. Для 10 и более троп будем решать
- 21. Правило УМНОЖЕНИЯЕсли объект а можно выбрать n
- 22. Задача 4 (№194 учебника) Сколько трёхзначных чисел
- 23. Задача 5.В турнире участвовало 6 шахматистов. Сколько
- 24. Решение:1. Закодируем игроков числами от 1 до
- 25. Человек, пришедший в гости, забыл код, открывающий
- 26. Решение:0001 0010 0100 1000
- 27. Задачи, в которых дается какое-то количество элементов
- 28. Правило СУММЫ Если объект а
- 29. Формирование умений и навыков
- 30. Правила работы в группе:Решить в тетради
- 31. Задача 1 (№ 24)Государственные флаги некоторых стран
- 32. Задача 2Витя, Толя и Игорь купили вместе
- 33. Задача 3Поэт-модернист написал стихотворение, в котором первая
- 34. Задача 4Трое господ при входе в ресторан
- 35. Человек забыл код, открывающий замок на его
- 36. Задача 6В классе три человека хорошо поют,
- 37. Задача 7Имеется ткань двух цветов: голубая и
- 38. Задача 8У ученика в тетради нарисован прямоугольник,
- 39. Задача 9. Фирма владеет четырьмя магазинами. Кассир
- 40. Задача 10.На обед в школьной столовой предлагается
- 41. Решение задачи № 1
- 42. Решение задачи №2*ВИТТВВТВВИИТТИИВТИ ВИТ ТВИ ТИВ
- 43. Решение задачи № 3Хочу
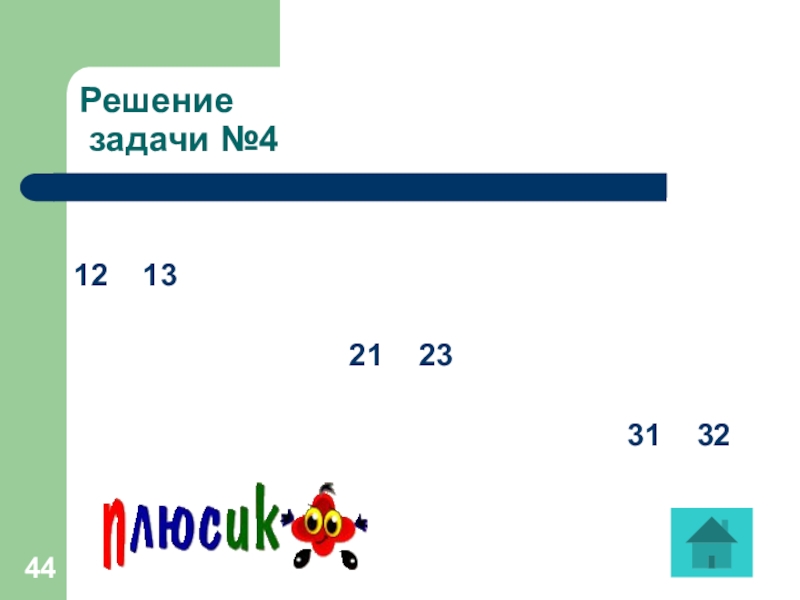
- 44. Решение задачи №412 13
- 45. Решение задачи № 5123 124
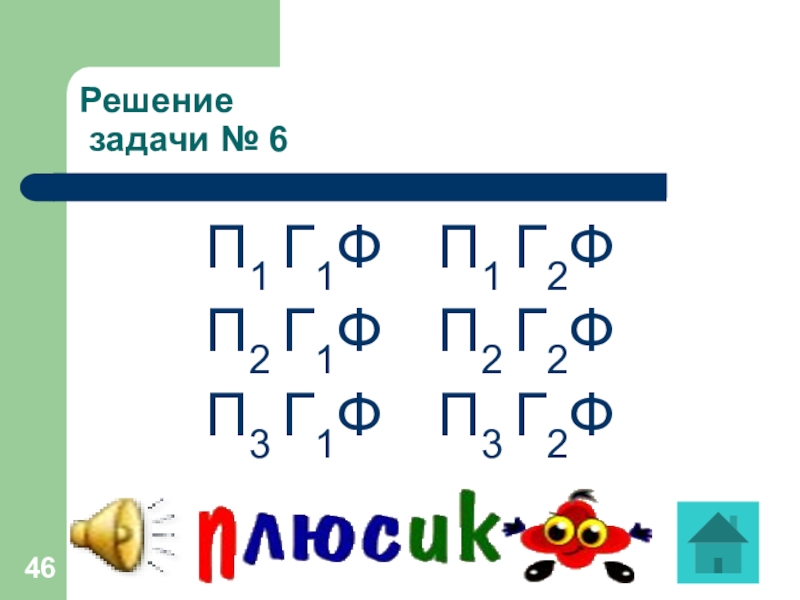
- 46. Решение задачи № 6 П1 Г1Ф
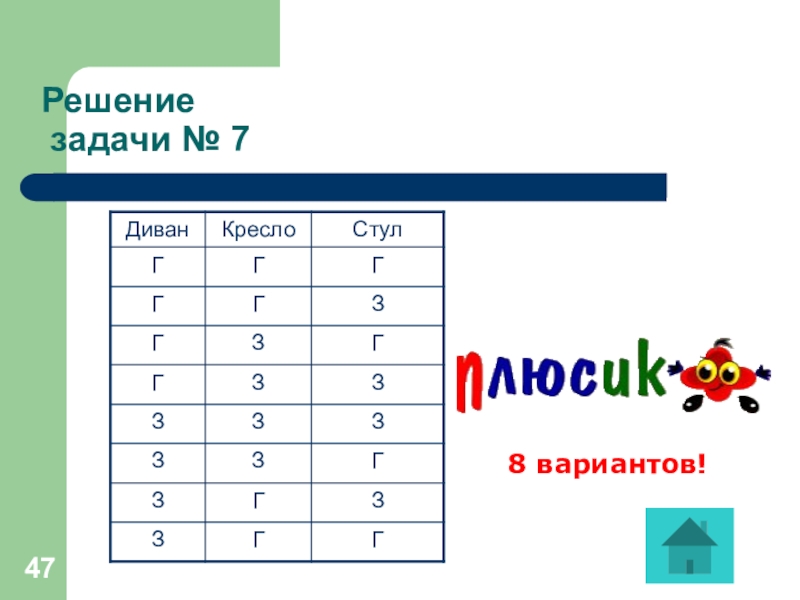
- 47. Решение задачи № 78 вариантов!
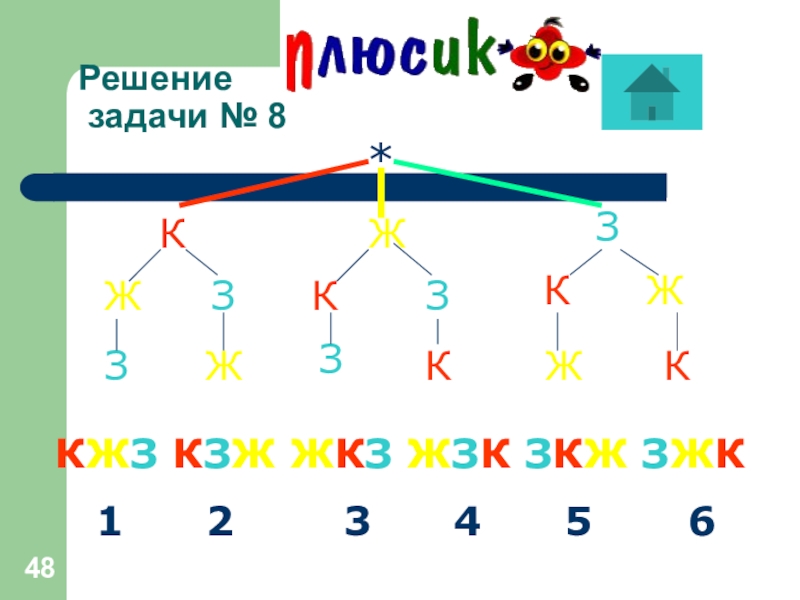
- 48. Решение задачи № 8*КЗЖЖККЖККЗЗЖЖЗЗКЖЗ КЗЖ ЖКЗ
- 49. Решение задачи № 9Все маршруты начинаются и
- 50. Решение задачи № 10Дерево вариантов «правильное»Ответ: 2∙3∙4=24 варианта *
- 51. Домашнее задание
- 52. Два курьера фирмы должны забрать почту из
- 53. Итоги урока
- 54. Ответьте на вопросыКакие обозначения удобно вводить
- 55. Ответьте на вопросыКак решаются задачи на
- 56. Малыш, гуляя, случайным образом перебирает различные варианты
- 57. МОЛОДЦЫ!
- 58. Цели и задачи:воспитательные:умение работать в группе,ответственность,дружелюбие, готовность
- 59. Цели и задачи:образовательные: Повторение материала 5 класса:
- 60. План урокаОрганизационный момент;Тестирование;Изучение нового материала;Работа в группе по формированию умений навыков;Итоги урока;Домашнее задание.
Как говорят о событиях, которые в данных условиях обязательно наступят? ДОСТОВЕРНЫЕникогда не наступят? НЕВОЗМОЖНЫЕмогут наступить, а могут и не наступить? СЛУЧАЙНЫЕ
Слайд 2Как говорят о событиях,
которые в данных условиях
обязательно наступят?
ДОСТОВЕРНЫЕ
никогда
не наступят?
НЕВОЗМОЖНЫЕ
могут наступить, а могут и не наступить?
СЛУЧАЙНЫЕ
НЕВОЗМОЖНЫЕ
могут наступить, а могут и не наступить?
СЛУЧАЙНЫЕ
Слайд 3Какое
это событие?
Черепаха научится говорить
невозможное
Вода в чайнике закипит
случайное
Вы нажали на
звонок, а он не зазвонил
случайное
День рождения вашего друга 30 февраля
невозможное
случайное
День рождения вашего друга 30 февраля
невозможное
В году не меньше 365 дней
достоверное
Подкинули монету и она упала на землю «орлом»
случайное
1 июня в Воронеже будет снег
невозможное
1 июня в Воронеже ночь короче дня
достоверное
Слайд 5_______________________________________________________________
Фамилия Имя Класс
Вариант (1 или 2)
Слайд 6№1. Выберите верное предложение I вариант
II вариант
Достоверное событие это: Невозможное событие это:
Событие, которое в данном опыте обязательно наступит
Событие, которое в данном опыте наступить не может
Событие, которое в данном опыте может наступить, а может и не наступить
Слайд 7
№ 2. Выберите достоверное событие из предложенных
I вариант
Вы
нажали звонок и он не зазвонил
День рождения вашего друга 30 февраля
Ель - вечнозелёное дерево
День рождения вашего друга 30 февраля
Ель - вечнозелёное дерево
II вариант
Вода в чайнике закипит
Черепаха научится говорить
Государственный флаг России имеет три цвета
Слайд 8№ 3. Выберите невозможное событие из предложенных
I вариант
1 июня в
Воронеже день короче ночи
Черепаха научится говорить
Вы нажали звонок и он не зазвонил
Черепаха научится говорить
Вы нажали звонок и он не зазвонил
II вариант
Вода в чайнике закипит
День рождения вашего друга 30 февраля
В году не меньше 365 дней
Слайд 9
№ 4. Выберите случайное событие из предложенных
I вариант
Мой
друг не пришёл в школу
В году не меньше 365 дней
Черепаха научится говорить
В году не меньше 365 дней
Черепаха научится говорить
II вариант
Вы нажали звонок и он не зазвонил
1 июня в Воронеже день короче ночи
День рождения вашего друга 30 февраля
Слайд 10№ 5. Вставьте нужное слово в определение
(«достоверным», «невозможным», «случайным»)
I вариант
Событие,
которое в данном опыте может наступить, а может и не наступить называется _________________
II вариант
Событие, которое в данном опыте обязательно наступит называется __________________
Слайд 13Малыш, гуляя, случайным образом перебирает различные варианты развлечений (велосипед, горка, тоннель,
кубики, лужайка).
Подсчитайте все виды игр ребёнка.
Ответ: 5
А сколькими способами можно разнообразить эту прогулку?
Слайд 14КОМБИНАТОРИКА – это раздел математики, посвященный решению задач на перебор различных
вариантов, удовлетворяющих каким-либо правилам или условиям.
Блез Паскаль
Пьер Ферма
Слайд 15Блез Паскаль
(1623-1662)
Пьер Ферма
(1601-1665)
Якоб Бернули
(1654-1705)
Готфрид Лейбниц
(1646-1716)
Слайд 16Задача 1
Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции,
Рима и Флоренции. Сколько существует вариантов такого маршрута?
Слайд 18Задача 2.
От турбазы к горному озеру ведут 4ре тропы (10 троп).
Сколькими способами туристы могут отправиться к озеру и вернуться обратно, если они не хотят спускаться по той же тропе по которой поднимались?
Решение:
Занумеруем тропы числами от 1 до 4;
Построим дерево возможных вариантов;
На подъёме к озеру 4 «узла»;
Из каждого «узла» выходят 3 ветки (спуск по 3м остальным тропам).
Решение:
Занумеруем тропы числами от 1 до 4;
Построим дерево возможных вариантов;
На подъёме к озеру 4 «узла»;
Из каждого «узла» выходят 3 ветки (спуск по 3м остальным тропам).
Слайд 19Дерево возможных вариантов
*
*
1
2
3
4
2
3
4
1
3
4
1
2
4
1
2
3
Всего 4∙3=12 маршрутов похода к озеру.
П о
д ъ ё м
С п у с к
1 2 3 4 5 6 7 8 9 10 11 12
Слайд 20Для 10 и более троп будем решать задачу рассуждением, т.к изобразить
её сложнее.
1) Поднимаемся по любой из 10 троп.
2) Спускаемся по любой из оставшихся 9 троп.
Итак: всего получим 10∙9 =90 различных маршрутов.
Такой способ подсчета возможен, если дерево вариантов «правильное»:, из каждого «узла» одного уровня выходит одно и тоже число веток.
Ответ получается умножением.
Слайд 21Правило УМНОЖЕНИЯ
Если объект а можно выбрать n способами, а объект b
выбрать m способами, то выбор пары
«а и b» можно осуществить
(n · m) способами.
«а и b» можно осуществить
(n · m) способами.
Слайд 22Задача 4 (№194 учебника)
Сколько трёхзначных чисел можно составить из чётных
цифр?
Решение:
0, 2, 4, 6, 8 - чётные цифры.
Ц ифра 0 первой быть не может, значит, имеется 4 варианта первой цифры.
Вторую цифру можно выбрать пятью способами.
Третью – также пятью способами.
Ответ: 4∙5∙5=100 трёхзначных чисел.
(п.с. Дерево вариантов «правильное»)
Решение:
0, 2, 4, 6, 8 - чётные цифры.
Ц ифра 0 первой быть не может, значит, имеется 4 варианта первой цифры.
Вторую цифру можно выбрать пятью способами.
Третью – также пятью способами.
Ответ: 4∙5∙5=100 трёхзначных чисел.
(п.с. Дерево вариантов «правильное»)
Слайд 23Задача 5.
В турнире участвовало 6 шахматистов. Сколько сыграно партий, если каждый
из них сыграл с каждым из остальных по одной партии?
(дерево вариантов неправильное, т.е. задача не может решаться по правилу умножения)
(дерево вариантов неправильное, т.е. задача не может решаться по правилу умножения)
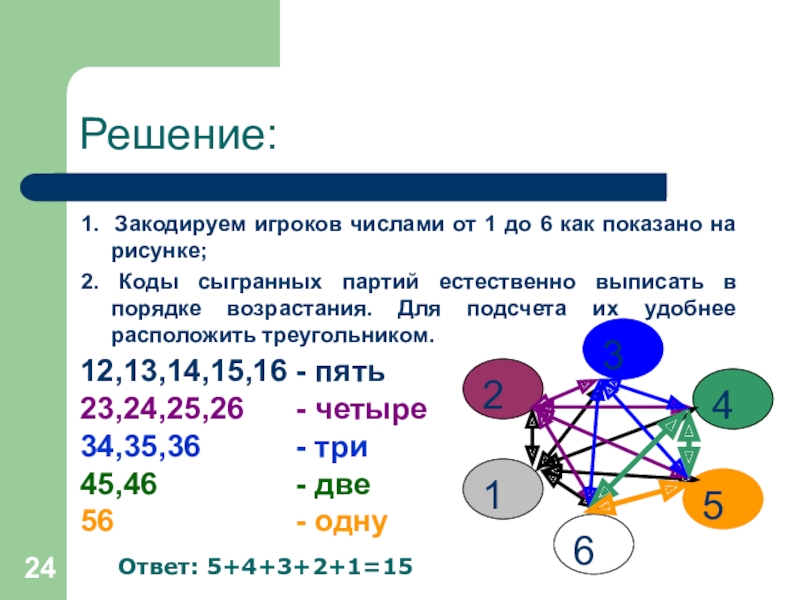
Слайд 24Решение:
1. Закодируем игроков числами от 1 до 6 как показано на
рисунке;
2. Коды сыгранных партий естественно выписать в порядке возрастания. Для подсчета их удобнее расположить треугольником.
2. Коды сыгранных партий естественно выписать в порядке возрастания. Для подсчета их удобнее расположить треугольником.
2
3
4
5
6
1
12,13,14,15,16 - пять
23,24,25,26 - четыре
34,35,36 - три
45,46 - две
56 - одну
Ответ: 5+4+3+2+1=15
Слайд 25
Человек, пришедший в гости, забыл код, открывающий дверь подъезда, но помнил,
что он составлен из нулей и единиц и содержит четыре цифры. Сколько вариантов
кода в худшем случае ему
придется перебрать, чтобы
открыть дверь?
кода в худшем случае ему
придется перебрать, чтобы
открыть дверь?
Задача 6
Слайд 26Решение:
0001 0010 0100 1000
- 4 варианта
0011 0101 0110 1001 1010 1100 - 6 вариантов
0111 1011 1101 1110 - 4 варианта
Всего: 4+6+4=14 попыток!
0011 0101 0110 1001 1010 1100 - 6 вариантов
0111 1011 1101 1110 - 4 варианта
Всего: 4+6+4=14 попыток!
Слайд 27
Задачи, в которых дается какое-то количество элементов и требуется подсчитать число
всевозможных перестановок, называются задачами на перестановки
Замену предметов их условными обозначениями называют кодированием
Замену предметов их условными обозначениями называют кодированием
Слайд 28
Правило СУММЫ
Если объект а можно выбрать n способами,
а объект b выбрать m способами, то выбор
«или а или b» можно осуществить
(n + m) способами.
«или а или b» можно осуществить
(n + m) способами.
Слайд 30Правила
работы в группе:
Решить в тетради предложенные задачи.
Красочно оформить их средствами
ИКТ.
Защитить предложенное решение.
Воспитательные цели урока:
умение работать в группе,
ответственность,
дружелюбие,
готовность к дискуссии,
стремление к достижению хороших результатов
Защитить предложенное решение.
Воспитательные цели урока:
умение работать в группе,
ответственность,
дружелюбие,
готовность к дискуссии,
стремление к достижению хороших результатов
Слайд 31Задача 1 (№ 24)
Государственные флаги некоторых стран состоят из трех горизонтальных
полос разного цвета. Сколько существует различных вариантов флагов с белой, синей и красной полосой? Есть ли среди них флаг Российской Федерации?
Проверь себя!
Проверь себя!
Проверь себя!
Слайд 32Задача 2
Витя, Толя и Игорь купили вместе интересную книгу и решили
ее читать по очереди. Выпишите все варианты такой очереди. Сколько есть вариантов, в которых Игорь на первом месте? Витя не на последнем месте?
Проверь себя!
Слайд 33Задача 3
Поэт-модернист написал стихотворение, в котором первая строчка – «Хочу пойти
гулять куда-нибудь», а остальные строки все разные и получены из первой перестановкой слов. Какое наибольшее количество строк может быть в этом стихотворении?
Указание: В строке 4 разных слова, закодируйте их цифрами.
Указание: В строке 4 разных слова, закодируйте их цифрами.
Проверь себя!
Слайд 34Задача 4
Трое господ при входе в ресторан отдали швейцару свои шляпы,
а при выходе получили обратно. Сколько существует вариантов, при которых каждый из них получит чужую шляпу?
Проверь себя!
Слайд 35Человек забыл код, открывающий замок на его чемодане, но вспомнил, что
код состоит из трёх различных цифр, каждая из которых, больше трёх. Кроме того, в код точно не входит сочетание 13. Сколько вариантов кода в худшем случае ему придется перебрать, чтобы открыть свой чемодан?
Проверь себя!
Задача 5
Слайд 36Задача 6
В классе три человека хорошо поют, двое других играют на
гитаре, а еще один умеет показывать фокусы. Сколькими способами можно составить концертную бригаду из певца, гитариста и фокусника?
Проверь себя!
Слайд 37Задача 7
Имеется ткань двух цветов: голубая и зеленая – и требуется
обить диван, кресло и стул. Сколько существует различных вариантов обивки этой мебели?
Проверь себя!
Слайд 38Задача 8
У ученика в тетради нарисован прямоугольник, разделенный на три равные
части. Он должен закрасить каждую из этих частей в один из трех цветов: красный, желтый, зеленый. Нельзя окрашивать разные части одинаковым цветом. Сколько вариантов рисунка может получиться?
Проверь себя
Слайд 39Задача 9. Фирма владеет четырьмя магазинами. Кассир магазина №1 должен собрать
выручку и вернуться обратно. Выбрать самый короткий маршрут.
5,3 км
3,8 км
2,3 км
4 км
3,5 км
3,2 км
№2
№1
№4
№3
ответ
Слайд 40Задача 10.
На обед в школьной столовой предлагается 2 супа, 3 вторых
блюда и 4 различных сока. Сколько различных вариантов обеда из трёх блюд можно составить по данному меню?
ответ
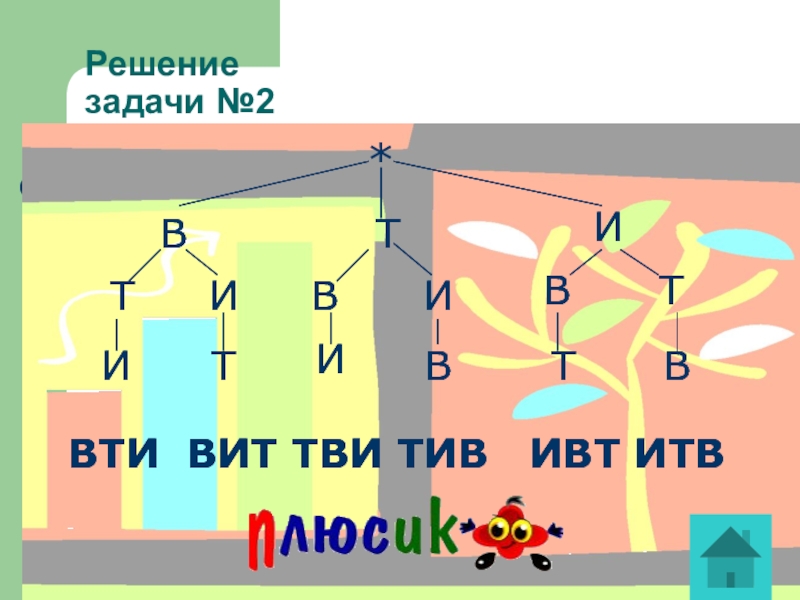
Слайд 42Решение
задачи №2
*
В
И
Т
Т
В
В
Т
В
В
И
И
Т
Т
И
И
ВТИ ВИТ ТВИ ТИВ ИВТ ИТВ
В
И
Т
Т
В
В
Т
В
В
И
И
Т
Т
И
И
ВТИ ВИТ ТВИ ТИВ
ИВТ ИТВ
В
И
Т
Т
В
В
Т
В
В
И
И
Т
Т
И
И
ВТИ ВИТ ТВИ ТИВ ИВТ ИТВ
Слайд 43
Решение
задачи № 3
Хочу пойти гулять куда-нибудь
Хочу пойти куда-нибудь гулять
Хочу гулять
пойти куда-нибудь
Хочу гулять куда-нибудь пойти
Хочу куда-нибудь пойти гулять
Хочу куда-нибудь гулять пойти
Пойти хочу гулять куда-нибудь
Пойти хочу куда-нибудь гулять
Пойти гулять хочу куда-нибудь
Пойти гулять куда-нибудь хочу
Пойти куда-нибудь хочу гулять
Пойти куда-нибудь гулять хочу
Хочу гулять куда-нибудь пойти
Хочу куда-нибудь пойти гулять
Хочу куда-нибудь гулять пойти
Пойти хочу гулять куда-нибудь
Пойти хочу куда-нибудь гулять
Пойти гулять хочу куда-нибудь
Пойти гулять куда-нибудь хочу
Пойти куда-нибудь хочу гулять
Пойти куда-нибудь гулять хочу
Гулять хочу пойти куда-нибудь
Гулять хочу куда-нибудь пойти
Гулять пойти хочу куда-нибудь
Гулять пойти куда-нибудь хочу
Гулять куда-нибудь хочу пойти
Гулять куда-нибудь пойти хочу
Куда-нибудь хочу пойти гулять
Куда-нибудь хочу гулять пойти
Куда-нибудь пойти хочу гулять
Куда-нибудь пойти гулять хочу
Куда-нибудь гулять хочу пойти
Куда-нибудь гулять пойти хочу
Слайд 45Решение
задачи № 5
123 124 132 134
142 143
213 214 231 234 243 241
312 314 321 324 341 342
412 413 421 423 431 432
20 кодов!
213 214 231 234 243 241
312 314 321 324 341 342
412 413 421 423 431 432
20 кодов!
Слайд 49Решение
задачи № 9
Все маршруты начинаются и заканчиваются 1.
12341, 12431, 13241, 13421,
14231, 14321,
т. е всего шесть маршрутов.
Подсчитаем расстояние.
5,3+4+3,5+3,2=16 (км) 5,3+3,8+3,5+2,3=14,9 (км)
2,3+4+3,8+3,2=13,3 (км) 2,3+3,5+3,8+5,3=14,9 (км)
3,2+3,8+4+2,3=13,3 (км) 3,2+3,5+4,5,3=16 (км)
Ответ: 13,3 км, если 13241 или 14231.
т. е всего шесть маршрутов.
Подсчитаем расстояние.
5,3+4+3,5+3,2=16 (км) 5,3+3,8+3,5+2,3=14,9 (км)
2,3+4+3,8+3,2=13,3 (км) 2,3+3,5+3,8+5,3=14,9 (км)
3,2+3,8+4+2,3=13,3 (км) 3,2+3,5+4,5,3=16 (км)
Ответ: 13,3 км, если 13241 или 14231.
Слайд 52
Два курьера фирмы должны забрать почту из четырех филиалов, причем каждый
успеет съездить только в два филиала из четырех. Сколькими способами они смогут распределить между собой поездки?
№53,80,81,100,108,137,160,232,262,293,355,410,517 – учебника
(любые 3 задачи).
Слайд 54Ответьте
на вопросы
Какие обозначения удобно вводить при решении комбинаторных задач?
Ответ: Обозначают
или кодируют предметы их первыми буквами названий или имён;
буквами с индексами, если имена или названия повторяются или совпадают;
нумеруют цифрами от 1 до n.
В чем состоит особенность задач на перестановки?
Ответ: В таких задачах производят подсчёт различных вариантов.
буквами с индексами, если имена или названия повторяются или совпадают;
нумеруют цифрами от 1 до n.
В чем состоит особенность задач на перестановки?
Ответ: В таких задачах производят подсчёт различных вариантов.
Слайд 55Ответьте
на вопросы
Как решаются задачи на перестановки?
Ответ: Составляют алгоритм решения в
виде графа, таблицы, дерева и пр., далее необходимо выяснить, дерево вариантов «правильное» или нет? Способы подсчёта вариантов – «умножение» или «сложение».
Сколько можно составить перестановок из трех элементов?
Ответ: Из трёх элементов можно сделать 6 перестановок. 3*2*1=6 или 3!=6.
Сколько можно составить перестановок из трех элементов?
Ответ: Из трёх элементов можно сделать 6 перестановок. 3*2*1=6 или 3!=6.
Слайд 56Малыш, гуляя, случайным образом перебирает различные варианты развлечений.
Итак виды игр
ребёнка – это велосипед, горка, тоннель, кубики, лужайка. Всего пять!
Так сколькими же способами можно разнообразить эту прогулку?
Так сколькими же способами можно разнообразить эту прогулку?
Ответ:
5! = 5∙4∙3∙2∙1=120 способов
Слайд 58Цели и задачи:
воспитательные:
умение работать в группе,
ответственность,
дружелюбие,
готовность к дискуссии,
стремление к
достижению хороших результатов
развивающие:
развитие познавательного интереса и эрудиции.
развивающие:
развитие познавательного интереса и эрудиции.
Слайд 59Цели и задачи:
образовательные:
Повторение материала 5 класса: случайные, достоверные и невозможные
события, «перебор различных вариантов», элементы кодирования информации и алгоритмизация;
Применение к решению задач «Правила умножения» и «Правила сложения»;
Применение к решению задач «Правила умножения» и «Правила сложения»;
Слайд 60План урока
Организационный момент;
Тестирование;
Изучение нового материала;
Работа в группе по формированию умений навыков;
Итоги
урока;
Домашнее задание.
Домашнее задание.
