- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Интересные свойства чисел
Содержание
- 1. Презентация Интересные свойства чисел
- 2. Содержание? Введение. ? Цель работы и задачи
- 3. Введение Число – одно из основных понятий математики,позволяющее
- 4. Потребность в измерениях привела к возникновению и
- 5. Цели работы и задачи по ее реализацииЦели:
- 6. Глава 1. Старинные системы записи чисел Современные цифры
- 7. В каменном веке, когда
- 8. Но до этого идеала человечество прошло
- 9. Иероглифическая система древних египтян
- 10. Для записи чисел использовали иероглифы:Означает: Две тысячи,
- 11. Уцелели два математических папируса, раскрывающие тайну древнеегипетского
- 12. Иератические (жреческие) цифры20
- 13. Вавилонские цифры Использовались клинообразные числовые знаки: вертикальная черточка – единица, угол – десять.
- 14. Числа от 1 до 59
- 15. Узловой счет индейцевСчет- узелки на шнурках разной
- 16. Цифры древнего народа майяЦифры – рисунки голов.
- 17. Позднее изображение чисел было упрощено. В изображении
- 18. В числовой системе майя:на первом месте стоят
- 19. Римские цифры Среди множества иероглифических систем счисления, которые
- 20. I V X
- 21. В римской нумерации используются принцип сложения и
- 22. Отличительные черты римской нумерации сравнению с нашей
- 23. В современной нумерации не только вид, начертание
- 24. Алфавитные системы Наряду
- 25. Славянские цифрычисла обозначались буквами, над которыми ставили особый знак титло
- 26. Способ обозначения больших цифр у славянДесять тысяч
- 27. Древние индийцыкаждая цифра – свой знак
- 28. Арабские цифрызаимствовали цифры у индийцев, упростили значки
- 29. Индийская нумерация пришла сначала в арабские страны,
- 30. Постепенное превращение первоначальных цифр в современные
- 31. Глава 2. Числовые диковинки В мире чисел, как
- 32. Оно замечательно прежде всего тем, что определяет
- 33. Любопытная особенность числа 999проявляется при умножении на
- 34. Число 1001 обладает рядом интересных свойств:является произведением
- 35. Число 1001 состоит из 77 «чертовых дюжин»
- 36. Число 10 101, так же как и
- 37. Число 10 001 проще двух предыдущих,
- 38. Глава 2. Числовые пирамиды Некоторые числа, хорошо всем
- 39. Пирамида 1. 1 х
- 40. Чтобы число вида 12 345… превратилось в
- 41. Пирамида 2. 1
- 42. Получение данного результата показано в следующем примере:Воспользовавшись
- 43. Пирамида 3. 9 х
- 44. Из первой пирамиды нам известно, что, например:
- 45. Заключение В ходе своего развития человечество стремилось совершенствовать
- 46. Мы проследили историю возникновения современных цифр,
- 47. Спасибо за внимание!
Слайд 2Содержание
? Введение.
? Цель работы и задачи по ее реализации.
? Глава
? Глава 2. Числовые диковинки.
? Глава 3. Числовые пирамиды.
? Заключение.
Слайд 3Введение
Число – одно из основных понятий математики,
позволяющее выразить результаты счета и
Цифры – условные знаки для обозначения цифр.
Считать люди научились еще в незапамятные времена.
Было время, когда человек умел считать только до двух.
Лишь постепенно человек научился считать до трех, затем
до пяти, десяти и т.д.
С развитием производства и торговли счет
распространяется на множества, содержащие все большее
и большее число предметов. Люди в своей практической
деятельности не могли обходиться без измерения
расстояний, площадей, земельных участков, вместимости
сосудов.
Слайд 4
Потребность в измерениях привела к возникновению и развитию как приемов измерений,
так
С древнейших времен люди интересовались свойствами чисел, выделяли среди них особенные. Некоторые, на первый взгляд обычные числа, записанные всем нам знакомыми цифрами, выделяются из ряда других какими-либо необычайными свойствами. Некоторые из них уже по внешности привлекают внимание, другие открывают свои диковинные особенности лишь при более близком знакомстве.
Слайд 5Цели работы и задачи по ее реализации
Цели: рассмотреть историю возникновения натуральных
Задачи:
показать необходимость введения цифр и чисел;
совершенствование их обозначения от каменного века до наших дней;
рассмотреть историю происхождения арабских цифр и найти преимущества записи чисел арабскими цифрами перед римскими;
исследовать свойства чисел 365, 999, 1001, 10 101, 10 001, 111 111, а также числовые пирамиды, рассмотреть применение этих свойств в устном счете.
Слайд 6Глава 1. Старинные системы записи чисел
Современные цифры были выработаны на протяжении
Слайд 7 В каменном веке, когда люди собирали плоды, ловили
Например, в 1937г. в Вестонице (Моравия) на месте одной из таких стоянок найдена волчья кость с 55 глубокими зарубками. Видно, что, делая эти зарубки, древний охотник считал по пальцам.
Слайд 8 Но до этого идеала человечество прошло путем
долгой эволюции, пользуясь гораздо
способами записи чисел.
Самая простая система записи чисел получила
название единичной, так как любое число в ней
образуется путем повторения одного знака,
символизирующего единицу.
Группировки и вспомогательные значки
Используются лишь для облегчения восприятия больших
чисел.
После того как в языке народа установился способ
называть числа, возникают поиски и создается система
письменного изображения этих чисел.
Система цифр у разных народов на разных ступенях
культурного развития были различны, начиная от зарубок
на деревянных палочках и кончая нашей десятичной
системой символов.
Слайд 9Иероглифическая система
древних египтян
В ней
ключевые
числа:
1, 10, 100 и т.д. - изображались
иероглифами.
Около 3 – 2,5 тыс. лет до н.э. древние египтяне придумали свою числовую систему.
Цифры- длинные знаки на папирусах
Слайд 10Для записи чисел использовали иероглифы:
Означает:
Две тысячи, три сотни, два десятка
1 10 102 103 104 105 106 107
Запись:
Слайд 11Уцелели два математических папируса, раскрывающие тайну древнеегипетского счета.
Один из них
«Папирусом Райнда»,
другой - «Московским папирусом»
«Московский папирус»
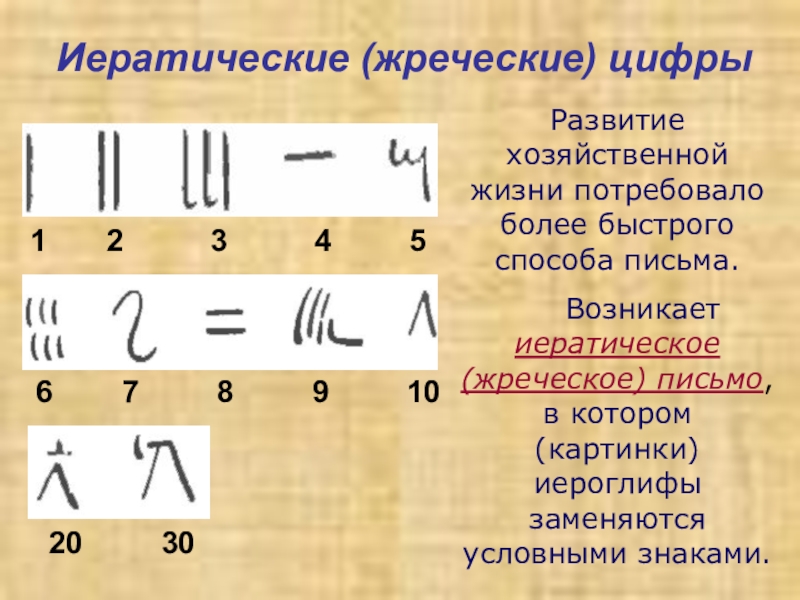
Слайд 12Иератические (жреческие) цифры
20 30
6
1 2 3 4 5
Развитие хозяйственной жизни потребовало более быстрого способа письма.
Возникает иератическое (жреческое) письмо, в котором (картинки) иероглифы заменяются условными знаками.
Слайд 13Вавилонские цифры
Использовались клинообразные числовые знаки: вертикальная черточка – единица, угол
Слайд 14 Числа от 1 до 59 записывались с помощью
Число 60 записывается тем же значком, что и 1, т.е .
Примеры записи чисел, больших 60:
Слайд 15Узловой счет индейцев
Счет- узелки на шнурках разной длины и цвета
Некоторые народы
Слайд 17Позднее изображение чисел было упрощено. В изображении чисел применяли пятеричную систему:
Система
В году у них содержалось 360 дней, которые делятся на 18 месяцев, по 20 дней в каждом.
Слайд 18В числовой системе майя:
на первом месте стоят единицы, далее
единицы второго разряда,
Единицей третьего разряда являются (18 ·20=)360 в соответствии с числом дней в году.
Отсутствие разряда указывалось специальным знаком , появившимся около 500 до н.э., в роде изображения глаза (наш нуль).
Слайд 19Римские цифры
Среди множества иероглифических систем счисления, которые существовали в разные времена
Ее цифры встречаются на циферблатах часов, фронтонах старинных и современных зданий. Речь идет о римской системе записи чисел.
Слайд 20I V X L c
1 5 10 50 100 500 1000
Некоторые из этих знаков служили и буквами.
Потребности практики, развитие производства и торговли способствовали созданию болеем удобных, современных цифр и образованию современной письменной нумерации
Вам известны римские цифры:
Запись числа 38784:
Слайд 21В римской нумерации используются принцип сложения и принцип вычитания; так, например,
пишут: для числа 9 вместо VIIII знак IV,
вместо XXXX знак XL и т.д.
Обозначение чисел римскими цифрами
Слайд 22Отличительные черты римской нумерации сравнению с нашей десятичной:
Записи длинные, умножение
Все действия надо производить в уме.
При прочтении числа необходимо складывать или вычитать, потому что каждая из семи римских цифр означает всюду, где бы она ни стояла, одно и то же число.
Например: V означает пять единиц, как в числе IV, так и в числеVI.
Слайд 23В современной нумерации не только вид, начертание цифры, но и
Например: В числе 15 цифра 5 означает пять единиц, а в числе 53 та же самая цифра означает пять десятков, т.е пятьдесят единиц. Отсюда нашу нумерацию называют позиционной.
Она, как и современные цифры, возникла примерно 1500 лет назад в Индии. В течение многих столетий, переходя от народа к народу, старинные индийские цифры много раз изменялись, пока приняли современную форму.
Слайд 24Алфавитные системы
Наряду с иероглифическими в
изображались буквами алфавита.
Именно такой была греческая алфавитная нумерация (ионическая).
В III в до н.э. она сменила аттическую.
Вместе с христианством и письменностью эта нумерация пришла к славянам.
Слайд 26Способ обозначения больших цифр у славян
Десять тысяч – тьма,
десять тем
десять легионов – леодр,
десять леодров – ворон,
десять воронов – колода
Слайд 29 Индийская нумерация пришла сначала в арабские страны, а затем и в
больших чисел, записанных в десятичной системе, сделали ее особенно популярной.
А поскольку труд аль-Хорезми был написан на общем для мусульманского мира языке – арабском, то за индийской нумерацией в Европе закрепилось неправильное название – «арабская»
аль-Хорезми
Слайд 31Глава 2. Числовые диковинки
В мире чисел, как и в мире живых
Из таких необыкновенных чисел можно было бы составить своего рода музей числовых редкостей
Слайд 32Оно замечательно прежде всего тем, что определяет число дней в году.
При
Другая особенность числа365:
365=10*10+11*11+12*12 т.е. 365 равно сумме квадратов трех последовательных чисел, начиная c 10.
Сумма квадратов двух следующих чисел 13 и 14 тоже равна 365.
13*13+14*14=169+196=365
Число 365
Слайд 33 Любопытная особенность числа 999
проявляется при умножении на него всякого
другого трехзначного числа.
Число 999
Зная эту особенность, можно мгновенно умножать трехзначное число на 999.
947◾999 = 946 053;
509◾999 = 508 491
и т.п.
Слайд 34Число 1001 обладает рядом интересных свойств:
является произведением тех простых чисел: 1001=7◾11◾13.
например: 873◾1001=873 873
Это свойство объясняется следующим: 873◾1001=873 ◾1000+873=873 000+873
1001=103+13;
Число 1001
Слайд 35Число 1001 состоит из 77 «чертовых дюжин» (1001=77∙13), из 91 одиннадцатки
Если будем считать, что год равен 52 неделям, то:
На свойствах числа 1001 основан метод определения делимости числа на 7, 11 и на 13.
348 285 = 348∙1000+285=348∙1000+(348-348)+285= = 348∙1001-(348-285).
Так как 1001 делится на 7, то чтобы число 348325 делилось на 7, достаточно, чтобы разность 348-285=63 делилась на 7.
Слайд 36Число 10 101, так же как и 1001, дает удивительный результат
Каждое двузначное число, умноженное на 10 101, дает в результате само себя, написанное трижды, например:
73◾10 101=737 373
Это свойство объясняется следующим:
Числа 10 101 и 10 001
Слайд 37
Число 10 001 проще двух предыдущих, оно представляет собой произведение
Каждое четырехзначное число, умноженное на 10 001, дает в результате само себя, написанное дважды, например:
3456◾10 001=34 563 456,так как:
Если же умножаем трехзначное число на 10 001, то в результате получим число, записанное дважды, но между этими двумя записями стоит 0, например: 345◾10 001=3 450 345
Слайд 38
Глава 2. Числовые пирамиды
Некоторые числа, хорошо всем знакомые, имеют очень
Иногда для записи чисел-множителей используются те же цифры, что и для записи произведения...
Слайд 39Пирамида 1.
1 х 9 + 2 =
12 х 9 + 3 = 111
123 х 9 + 4 = 1111
1234 х 9 + 5 = 11111
12345 х 9 + 6 = 111111
123456 х 9 + 7 = 1111111
1234567 х 9 + 8 = 11111111
12345678 х 9 + 9 = 111111111
Чтобы постичь данную числовую закономерность рассмотрим какой-нибудь из средних рядов нашей числовой пирамиды:
123456 х 9 + 7
Слайд 40 Чтобы число вида 12 345… превратилось в число вида 11 111…,
из второй его цифры вычесть 1,
из третьей – 2,
из четвертой – 3,
из пятой – 4 и т.д. Иначе говоря, вычесть из него то же число вида 12 345…, укороченное на свою последнюю цифру.
Слайд 41Пирамида 2.
1 х 8 + 1
12 х 8 + 2 = 98
123 х 8 + 3 = 987
1234 х 8 + 4 = 9876
12345 х 8 + 5 = 98765
123456 х 8 + 6 = 987654
1234567 х 8 + 7 = 9876543
12345678 х 8 + 8 = 98765432
123456789 х 8 + 9 = 987654321
Особенно интересна в пирамиде последняя строка, где в результате умножения на 8 и прибавления 9 происходит превращение цифр в такой же ряд, но записанных в обратном порядке: 123456789 х 8 + 9 = 987654321
Слайд 42 Получение данного результата показано в следующем примере:
Воспользовавшись особенностями Пирамиды 1
получаем,
То есть 12345 х 8 + 5 = 111 111 – 12 346= 98765
Слайд 43Пирамида 3.
9 х 9 + 7 =
98 х 9 + 6 = 888
987 х 9 + 5 = 8888
9876 х 9 + 4 = 88888
98765 х 9 + 3 = 888888
987654 х 9 + 2 = 8888888
9876543 х 9 + 1 = 88888888
98765432 х 9 + 0 = 888888888
Эта пирамида является следствием первых двух.
Слайд 44 Из первой пирамиды нам известно, что, например:
12 345 х 9
Умножив обе части на 8, получим:
(12 345 х 8 х 9) +(6 х 8) = 888 888.
Из второй пирамиды известно, что
12 345 х 8 + 5 = 98 765,
12 345 х 8 = 98 760,
Значит:
(12 345х8х9) +(6 х 8) = (98 760х9)+48=
= (98 760х9)+(5 х 9)+3= (98 760+5)х9+3=
=98 765х9+3
Слайд 45Заключение
В ходе своего развития человечество стремилось совершенствовать запись чисел, использовались различные
Слайд 46
Мы проследили историю возникновения современных цифр, а также возникновение современной
Были выявлены частные свойства чисел: 365, 1001, 10 101, 10 001, а также рассмотрено применение этих свойств в устном счете;
Мы рассмотрели числовые пирамиды и выявили закономерности их построения;
Рассмотрели особенности десятичной системы, выявили ее преимущества над другими системами (недесятичными).
В ходе проделанной работы: