- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад ИКТ на уроках математики
Содержание
- 1. Презентация ИКТ на уроках математики
- 2. Что такое ИКТКонец 20 – начало 21
- 3. Всё шире используются информационные технологии в образовательном
- 4. Теорема ПифагораПребудет вечной истина, как скороЕё познает
- 5. Содержание Формулировка теоремы Доказательства теоремы Значение теоремы Пифагора
- 6. Формулировка теоремы« Доказать, что квадрат, построенный
- 7. Современная формулировка« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
- 8. Доказательства теоремы Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.).
- 9. Самое простое доказательствоРассмотрим квадрат, показанный на рисунке. Сторона квадрата равна a + c. ca
- 10. В одном случае (слева) квадрат
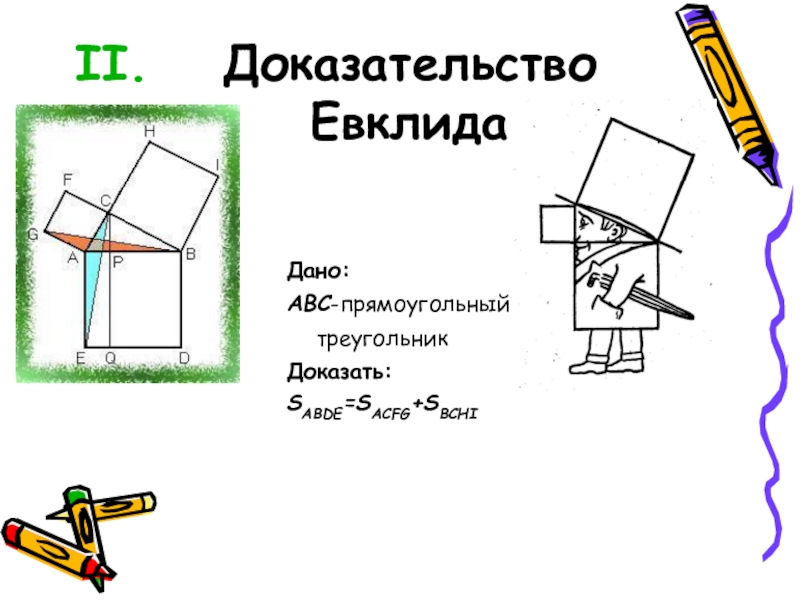
- 11. Доказательство Евклида Дано: ABC-прямоугольный треугольник Доказать:SABDE=SACFG+SBCHI
- 12. Доказательство: Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного
- 13. Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что
- 14. Алгебраическое доказательствоДано: ABC-прямоугольный треугольникДоказать: AB2=AC2+BC2 Доказательство: 1) Проведем высоту
- 15. Значение теоремы ПифагораТеорема Пифагора- это одна
- 16. Доказательство теоремы Пифагора учащиеся средних веков считали
- 17. Урок геометрии в 7 классе «Построение биссектрисы угла»
- 18. Построение биссектрисы угла
- 19. За горами, за лесами ,За
- 20. Звали старшего Данилой,Звали среднего Гаврилой,И, коль
- 21. Что тут делать, как тут быть?Как злодея
- 22. Треугольник очертили,Меж собой установили:Двое спят, а третий
- 23. K А FГлядь!... И обмер от испуга,В центре вписанного кругаСтранный конь без седокаПляшет в поле гопака.
- 24. Тут Иван перекрестился,Быстро Богу помолился,И хоть было не легко,Он подкрался к точке О.K А F О
- 25. Вывод:С помощью циркуля и линейки построили биссектрисы
- 26. Урок математики в 6 классе «Координатная плоскость»Астрономия на координатной плоскости
- 27. План проведения игры.Организационный момент.Созвездия на звездном небе.Зодиакальные
- 28. Зодиакальные созвездия.
- 29. Созвездия звёздного неба. Лебедь (лат. Cygnus, Cyg)
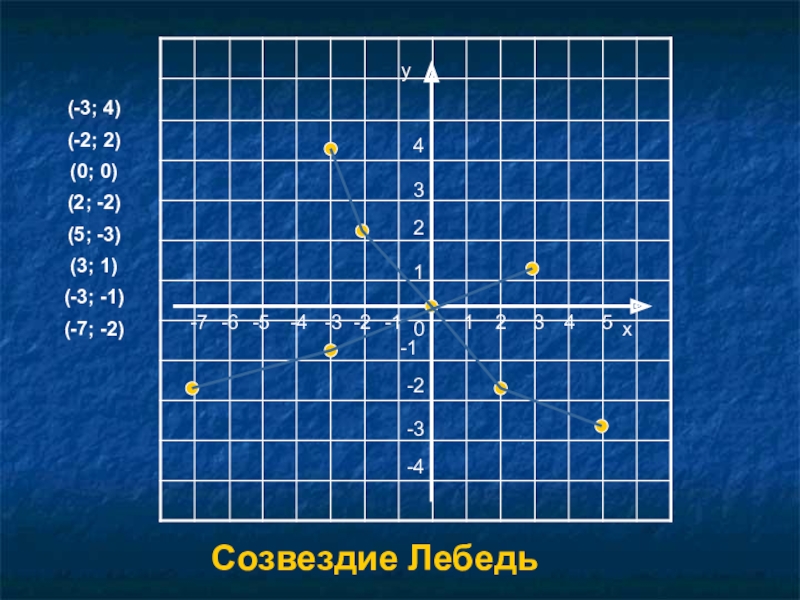
- 30. (-3; 4)(-2; 2)(0; 0)(2; -2)(5; -3)(3; 1)(-3; -1)(-7; -2)yx024-2-4-2-424Созвездие Лебедь1351-33-1-3-7-5-6-1
- 31. Что древние греки рассказывали о Медведицах?О Большой
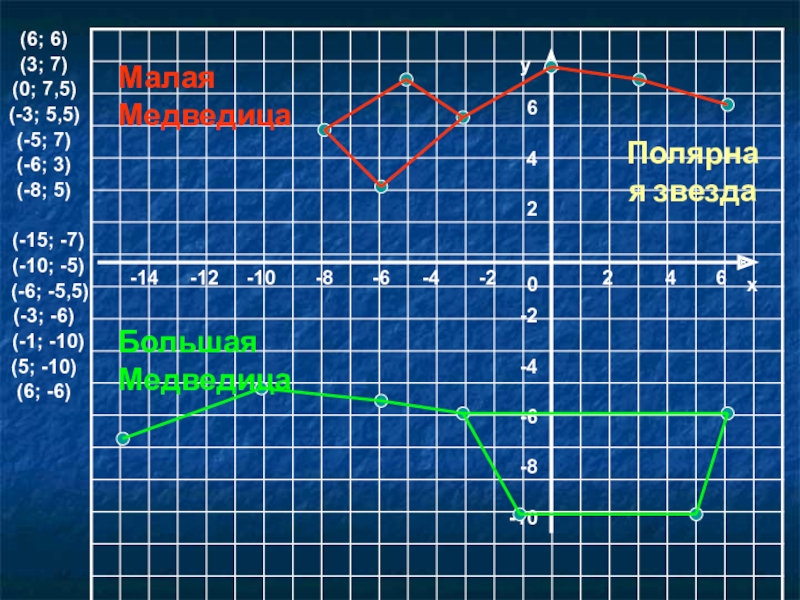
- 32. (6; 6)(3; 7)(0; 7,5)(-3; 5,5)(-5; 7)(-6; 3)(-8;
- 33. Применяя информационные технологии на уроках математики, учителям
Слайд 2Что такое ИКТ
Конец 20 – начало 21 века отмечены бурным развитием
За последние годы активной информатизации образования сложилась некоторая терминология, закрепившаяся в профессиональной сфере. Так стал общепринятым термин «информационно-коммуникационные технологии (ИКТ)», хотя в нём легко усмотреть некоторую повторяемость: наличие коммуникаций автоматически влечёт за собой обмен информацией, в то же время обмен информацией предполагает наличие коммуникаций.
Информационно-коммуникационные технологии предполагают использование компьютера для поиска, передачи, сохранения, структурирования и обработки информации.
Слайд 3
Всё шире используются информационные технологии в образовательном процессе, что повышает эффективность
мультимедийного наглядного пособия, тренажёра, средства диагностики и контроля. ИКТ можно использовать на различных этапах процесса обучения: при объяснении нового материала, закреплении, повторении, контроле, обобщении и систематизации, а также в домашних заданиях и внеклассной работе.
Слайд 4Теорема Пифагора
Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема
Верна, как и в его далёкий век.
Слайд 6Формулировка
теоремы
« Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик
« Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».
Во времена Пифагора теорема звучала так:
или
Слайд 7Современная формулировка
« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
Слайд 8Доказательства теоремы
Существует около 500 различных доказательств этой теоремы (геометрических,
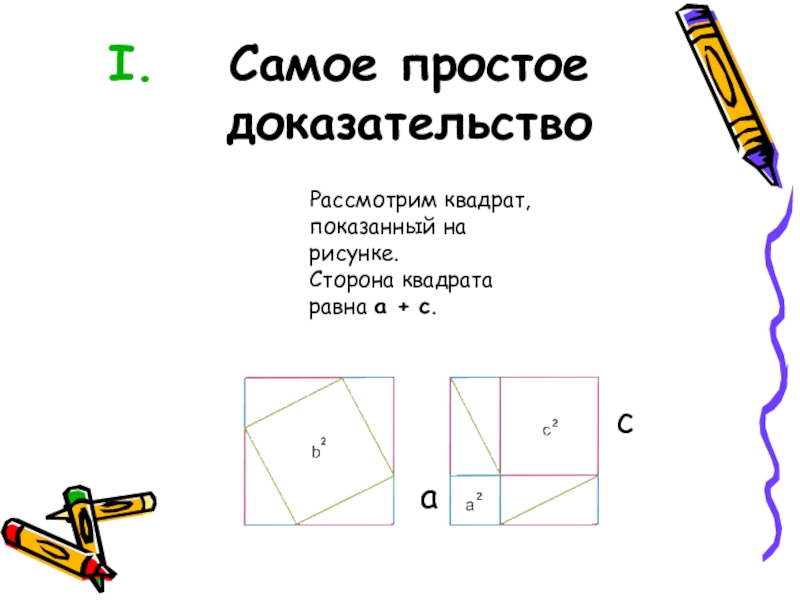
Слайд 9Самое простое доказательство
Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна a +
c
a
Слайд 10
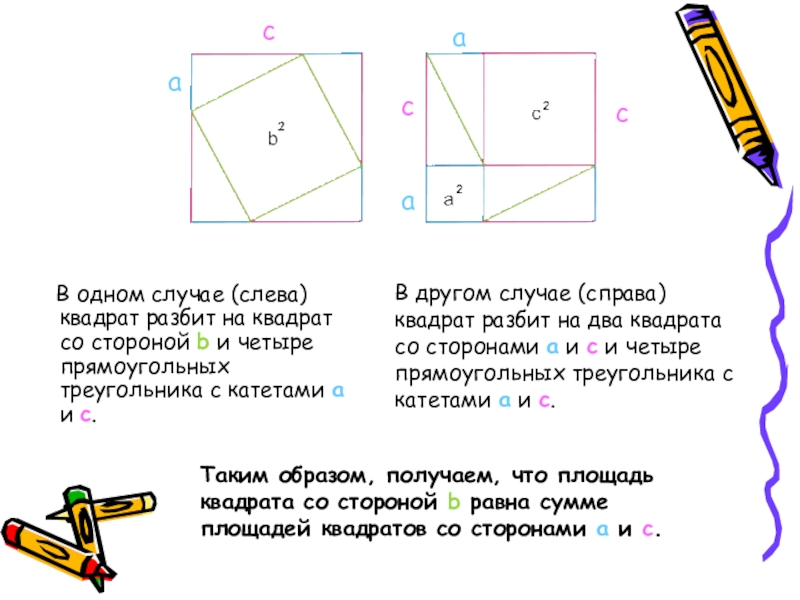
В одном случае (слева) квадрат разбит на квадрат со
a
c
a
c
В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.
a
c
Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.
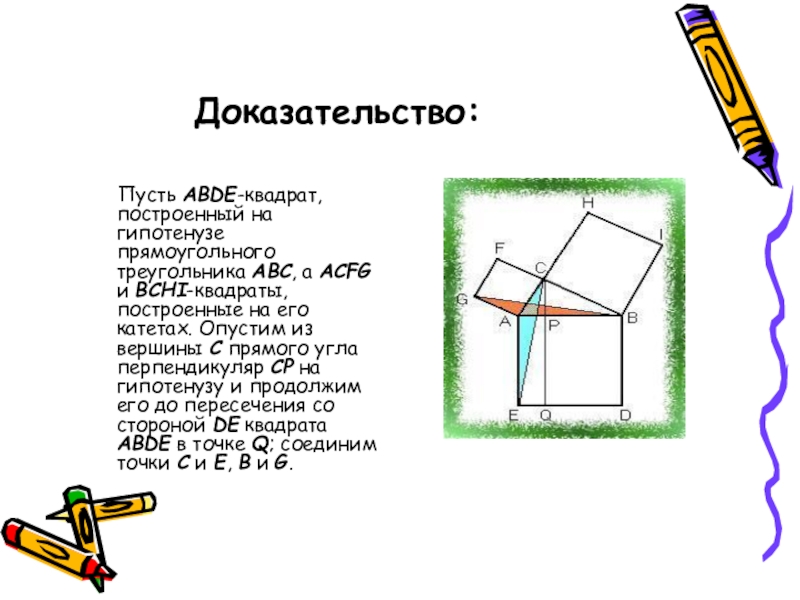
Слайд 12Доказательство:
Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного треугольника ABC, а ACFG
Слайд 13Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что треугольники ACE и AGB(закрашенные
SPQEA=2SACE
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, SFCAG=2SGAB
Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.
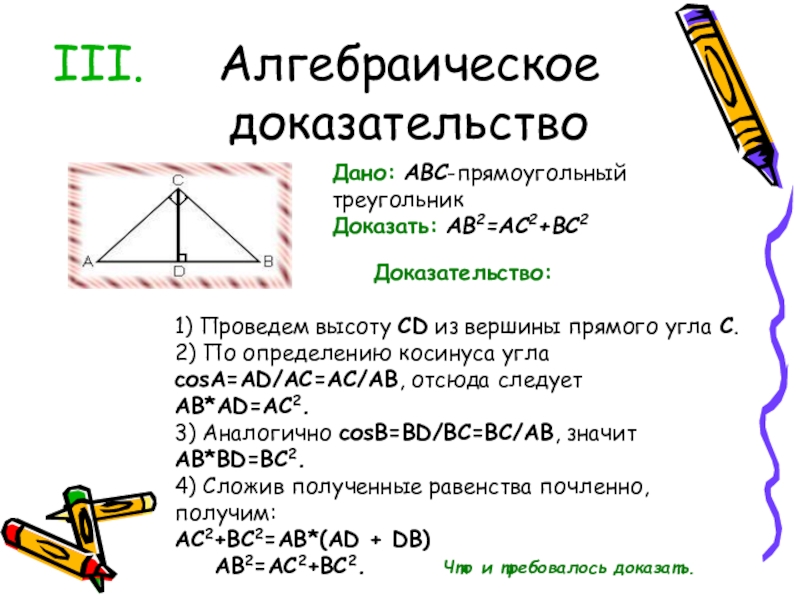
Слайд 14Алгебраическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: AB2=AC2+BC2
Доказательство:
1) Проведем высоту CD из вершины прямого угла
AB*AD=AC2.
3) Аналогично соsВ=BD/BC=BC/AB, значит
AB*BD=BC2.
4) Сложив полученные равенства почленно, получим:
AC2+BC2=АВ*(AD + DB)
AB2=AC2+BC2. Что и требовалось доказать.
Слайд 15 Значение теоремы Пифагора
Теорема Пифагора- это одна из самых важных теорем
Слайд 16Доказательство теоремы Пифагора учащиеся средних веков считали очень трудным и называли
Слайд 19За горами, за лесами ,
За широкими морями ,
Против
Жил старик в одном селе.
У старинушки три сына:
Старший умный был детина,
Средний сын и так и сяк,
Младший вовсе был дурак.
(П. П. Ершов «Конёк-Горбунок»)
Слайд 20Звали старшего Данилой,
Звали среднего Гаврилой,
И, коль это не обман,
Самый
Братья сеяли пшеницу
И возили за границу.
Ту пшеницу продавали
И карманы набивали…
Вдруг, случилась им беда
(Так бывает иногда), -
Кто-то в поле стал гулять
И пшеницу воровать.
Слайд 21Что тут делать, как тут быть?
Как злодея изловить?
Братья думали-рядили,
И в конце
Стал Данила в точке А,
Стал Гаврила в точке К,
А Иван, почистив хлев,
Притаился в точке F.
Слайд 22Треугольник очертили,
Меж собой установили:
Двое спят, а третий ждёт
Тех, кто ночью красть
В точке А уснул Данила,
В точке К уснул Гаврила,
В точке F Иван не спит,
Он пшеницу сторожит.
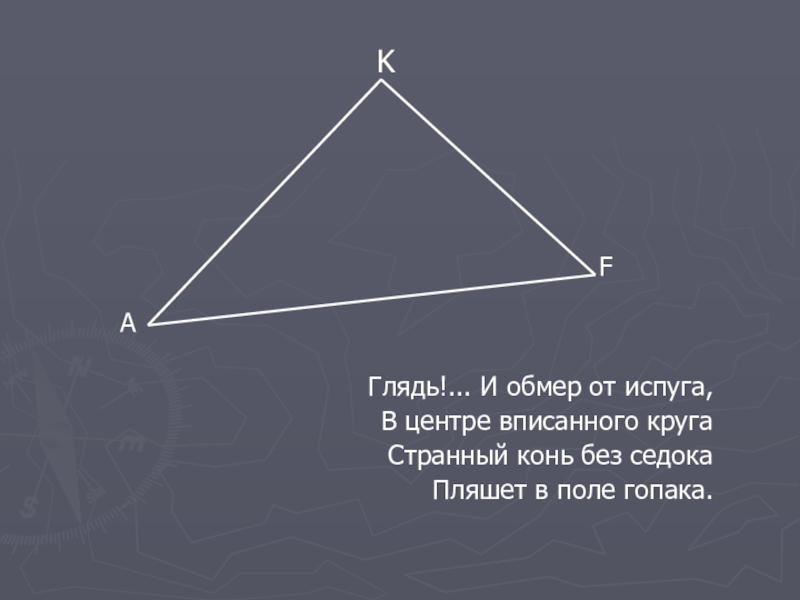
Слайд 23K
А
F
Глядь!... И обмер от испуга,
В центре вписанного круга
Странный конь
Пляшет в поле гопака.
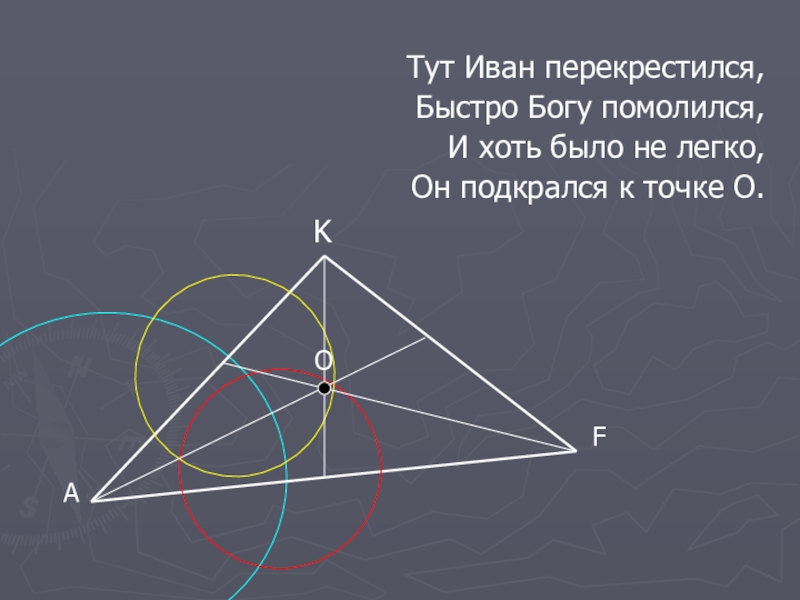
Слайд 24
Тут Иван перекрестился,
Быстро Богу помолился,
И хоть было не легко,
Он подкрался к
K
А
F
О
Слайд 25Вывод:
С помощью циркуля и линейки построили биссектрисы углов треугольника АKF. Биссектрисы
По теореме:
центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Слайд 27План проведения игры.
Организационный момент.
Созвездия на звездном небе.
Зодиакальные созвездия.
Легенда о Персее.
Легенда о
Биография Рене Декарта
Подведение итогов
Слайд 29Созвездия звёздного неба.
Лебедь (лат. Cygnus, Cyg) — созвездие северного полушария
Оптимальное время года для наблюдения — лето
Слайд 30(-3; 4)
(-2; 2)
(0; 0)
(2; -2)
(5; -3)
(3; 1)
(-3; -1)
(-7; -2)
y
x
0
2
4
-2
-4
-2
-4
2
4
Созвездие Лебедь
1
3
5
1
-3
3
-1
-3
-7
-5
-6
-1
Слайд 31Что древние греки рассказывали о Медведицах?
О Большой и Малой Медведицах существует
Слайд 32(6; 6)
(3; 7)
(0; 7,5)
(-3; 5,5)
(-5; 7)
(-6; 3)
(-8; 5)
(-15; -7)
(-10; -5)
(-6; -5,5)
(-3;
(-1; -10)
(5; -10)
(6; -6)
y
x
0
2
4
2
6
4
6
-2
-4
-6
-8
-10
-2
-4
-6
-8
-10
-12
-14
Малая Медведица
Большая Медведица
Полярная звезда
Слайд 33Применяя информационные технологии на уроках математики, учителям удалось добиться:
индивидуализировать учебный
Создать условия для развития самостоятельности учащихся;
Повысить качество наглядности в учебном процессе (презентации, построение сечений многогранников, построение графиков и т. д.).
Информационные технологии повышают информативность урока, эффективность обучения, придают уроку динамизм и выразительность.
Итогом внедрения ИКТ в образовательный процесс является позитивная динамика изменения мотивации учащихся.