неизвестными.
Развивать интегративное мышление учащихся.
Воспитывать информационно-математическую культуру учащихся и познавательную самостоятельность.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Графический способ решения систем уравнений
Содержание
- 1. Презентация Графический способ решения систем уравнений
- 2. Графический способ решения системы двух уравнений первой степени с двумя неизвестными
- 3. Этапы урока:Актуализация знаний учащихся ( учитель математики)Самостоятельное
- 4. Линейное уравнение с двумя переменными ах+bу+с=0Что называется
- 5. у=кх+mЭто частный вид линейного уравнения с двумя переменными, к и m – коэффициенты, причем к≠0
- 6. График линейной функцииу=кх+m – линейная функция, специальный
- 7. График линейной функцииГрафиком линейной функции y = kxявляется прямая, проходящая через начало координат.
- 8. Зависимая и независимая переменная6х+3у+18=0 → х и
- 9. Реши устно:Является ли решением уравнения х-2у=6
- 10. График линейного уравнения с двумя переменными ах+bу+с=0
- 11. Графический способ решения системы двух уравнений первой степени с двумя неизвестными
- 12. Система двух линейных уравнений с двумя неизвестными:а1х+b1у+с1=0,а2х+b2у+с2=0,
- 13. Решением системы двух уравнений с двумя неизвестными
- 14. Пример1у = 3х+2 – уравнение прямой, проходящей
- 15. Построим эти прямые в системе координат хОуПрямые
- 16. Пример 2.Решим графическим способом систему уравнений:х-у+1=0х-у+2=0
- 17. Решить графическим способом систему уравнений2х+2у-1=0-4х-4у+2=0
- 18. Разрешить каждое уравнение относительно у;Для решения системы
- 19. Решить графическим способом систему уравнений:
- 20. Гимнастика для глаз
- 21. Слайд 21
Графический способ решения системы двух уравнений первой степени с двумя неизвестными
Слайд 3Этапы урока:
Актуализация знаний учащихся
( учитель математики)
Самостоятельное изучение нового материала (
по презентации)
Закрепление изученного ( групповая работа с учителем математики)
Использование компьютера для решения заданий по данной теме (учитель информатики)
Самостоятельная работа ( по вариантам с учителем информатики)
Итоги урока (учитель математики)
Закрепление изученного ( групповая работа с учителем математики)
Использование компьютера для решения заданий по данной теме (учитель информатики)
Самостоятельная работа ( по вариантам с учителем информатики)
Итоги урока (учитель математики)
Слайд 4Линейное уравнение с двумя переменными ах+bу+с=0
Что называется решением уравнения с двумя
переменными?
Что является графиком линейного уравнения с двумя переменными?
Сколько необходимо точек для построения этого
графика?
Что значит, точка принадлежит графику линейного уравнения с двумя переменными?
Приведите пример линейного уравнения с двумя переменными
Слайд 5у=кх+m
Это частный вид линейного уравнения с двумя переменными, к и m
– коэффициенты, причем к≠0
Слайд 6График линейной функции
у=кх+m – линейная функция, специальный вид линейного уравнения с
двумя переменными.
Графиком линейной функции является прямая
Коэффициент k называется угловым коэффициентом этой прямой
При положительных k этот угол острый,
при отрицательных - тупой.
Слайд 7График линейной функции
Графиком линейной функции
y = kx
является прямая, проходящая через
начало координат.
Слайд 8Зависимая и независимая переменная
6х+3у+18=0 → х и у равноправны
у=2х+3 → у
зависит от х
Х – независимая переменная или аргумент,
У – зависимая переменная или функция.
Слайд 9Реши устно:
Является ли решением уравнения х-2у=6 пара чисел:
а) (0;0) в)
(8;1) д) (15;4)
б) (2;-2) г) (0;3) е) (6;0)
б) (2;-2) г) (0;3) е) (6;0)
Выразите переменную у через переменную х из уравнения:
а) х+у=1 б) 3х-у=2 в) 2х+5у=10
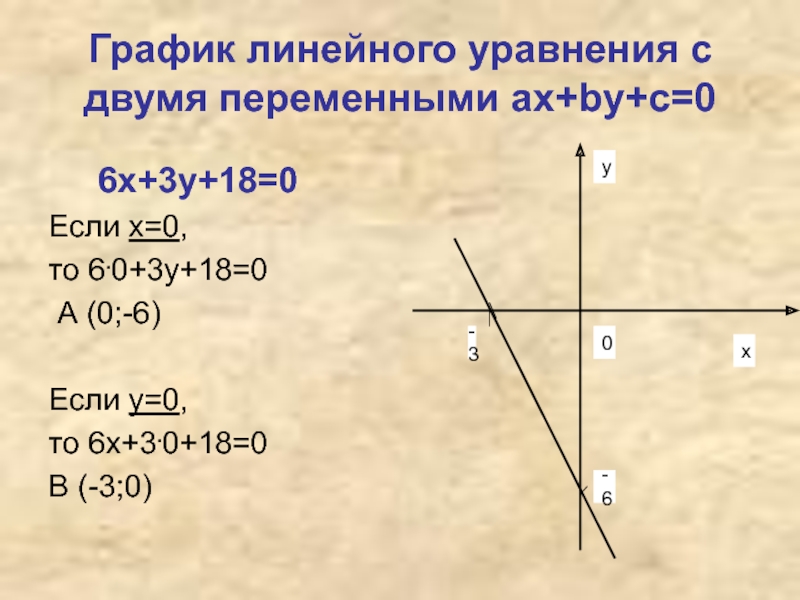
Слайд 10График линейного уравнения с двумя переменными ах+bу+с=0
6х+3у+18=0
Если х=0,
то 6.0+3у+18=0
А (0;-6)
Если у=0,
то 6х+3.0+18=0
В (-3;0)
Слайд 12Система двух линейных уравнений с двумя неизвестными:
а1х+b1у+с1=0,
а2х+b2у+с2=0,
где а1,b1,с1,а2,b2,с2 – заданные
числа,
а х и у - неизвестные
а х и у - неизвестные
Слайд 13Решением системы двух уравнений с двумя неизвестными называют такую пару чисел
Х и У, которые при подстановке в эту систему, обращают каждое ее уравнение в верное равенство.
Решить систему уравнений – это значит найти все ее решения или показать, что их нет.
Слайд 14Пример1
у = 3х+2 –
уравнение прямой, проходящей через точки А1(1;5) и
В1(0;2).
- уравнение прямой, проходящей через точки А2(1;-2) и В2(0;-3/2)
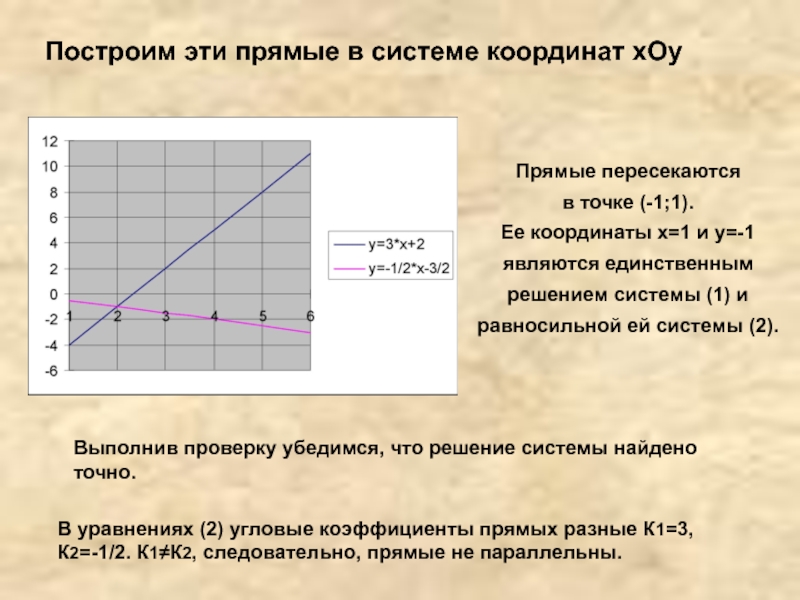
Слайд 15Построим эти прямые в системе координат хОу
Прямые пересекаются
в точке (-1;1).
Ее координаты х=1 и у=-1 являются единственным решением системы (1) и равносильной ей системы (2).
Выполнив проверку убедимся, что решение системы найдено точно.
В уравнениях (2) угловые коэффициенты прямых разные К1=3, К2=-1/2. К1≠К2, следовательно, прямые не параллельны.
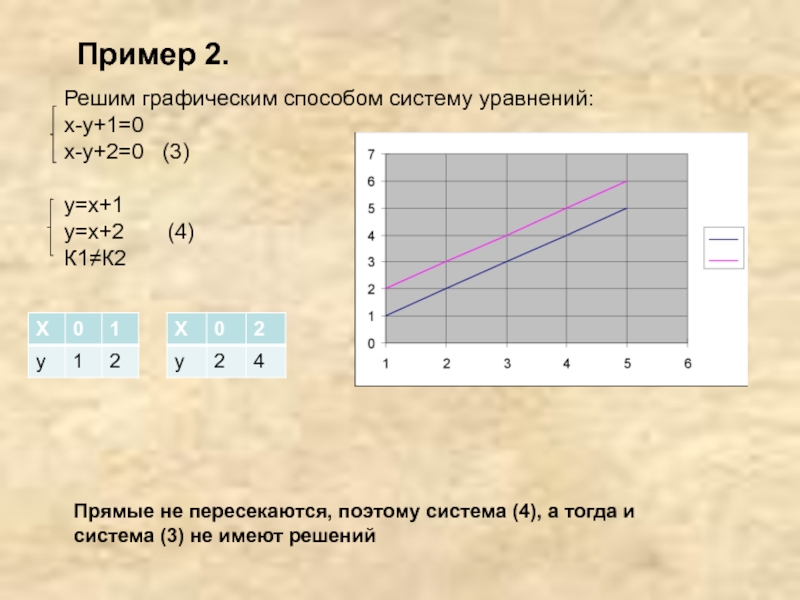
Слайд 16Пример 2.
Решим графическим способом систему уравнений:
х-у+1=0
х-у+2=0 (3)
у=х+1
у=х+2
(4)
К1≠К2
К1≠К2
Прямые не пересекаются, поэтому система (4), а тогда и система (3) не имеют решений
Слайд 17
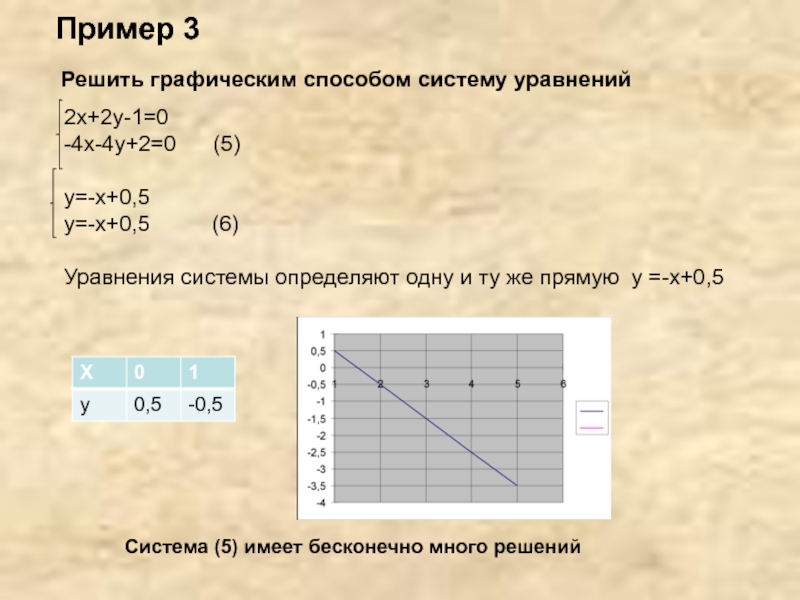
Решить графическим способом систему уравнений
2х+2у-1=0
-4х-4у+2=0 (5)
у=-х+0,5
у=-х+0,5
(6)
Уравнения системы определяют одну и ту же прямую у =-х+0,5
Уравнения системы определяют одну и ту же прямую у =-х+0,5
Система (5) имеет бесконечно много решений
Пример 3
Слайд 18Разрешить каждое уравнение относительно у;
Для решения системы линейных уравнений графическим способом
надо:
2. Построить на координатной плоскости прямые, соответствующие полученным уравнениям:
если прямые пересекаются, то координаты точки их пересечения и будут решением системы;
если прямые окажутся параллельными, то система не имеет решений;
если прямые совпадут, то система имеет много решений- множество пар координат точек этой прямой.
