МБОУ СОШ №11
Воротилина Екатерина
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад 1 для подготовки к ОГЭ по математике, задания № 21-26 (9 класс)
Содержание
- 1. Презентация 1 для подготовки к ОГЭ по математике, задания № 21-26 (9 класс)
- 2. Задание №21:Алгебраические выражения, уравнения, неравенства и их системыРешите неравенство (3x-2)(x+4)>-11
- 3. Решение :Раскроем скобки, приведём подобные слагаемые, разложим
- 4. Задание №22:Текстовые задачиИгорь и Паша красят забор
- 5. Решение:За один час Игорь и Паша красят
- 6. Задание№23: Функции и их свойства. Графики функцийПостройте
- 7. Решение:Построим график функцииИз графика видно, что прямая
- 8. Задание№24:Геометрическая задача на вычислениеБиссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF = 24, BF = 10.
- 9. Решение:Сумма углов, прилежащих к боковой стороне трапеции,
- 10. Задание№25: Геометрическая задача на доказательствоТри стороны параллелограмма
- 11. Решенеие:В параллелограмме противоположные стороны равны, поэтому если
- 12. Задание№26: Геометрическая задача повышенной сложностиПрямая, параллельная основаниям
- 13. Решение:Проведём построения и введём обозначения как показано
Задание №21:Алгебраические выражения, уравнения, неравенства и их системыРешите неравенство (3x-2)(x+4)>-11
Слайд 2Задание №21:Алгебраические выражения, уравнения, неравенства и их системы
Решите неравенство
(3x-2)(x+4)>-11
Слайд 3Решение :
Раскроем скобки, приведём подобные слагаемые, разложим на множители:
(3x-2)(x+4)>-11
3х²+10x+3>0
3(x+1/3)(x+3)>0
Произведение двух сомножителей
будет больше нуля, если сомножители имеют одинаковый знак (см. рисунок). Таким образом, получаем ответ:
(-∞;-3) U(-1/3; ∞)
(-∞;-3) U(-1/3; ∞)
Слайд 4Задание №22:Текстовые задачи
Игорь и Паша красят забор за 18 часов. Паша
и Володя красят этот же забор за 20 часов, а Володя и Игорь — за 30 часов. За сколько минут мальчики покрасят забор, работая втроём?
Слайд 5Решение:
За один час Игорь и Паша красят 1/18 забора, Паша и
Володя красят 1/20 забора, а Володя и Игорь — за 1/30 забора. Работая вместе, за один час два Игоря, Паши и Володи покрасили бы:
1/18+1/20+1/30=50/360=5/36 забора.
Тем самым, они могли бы покрасить один забор за 7,2 часа. Поскольку каждый из мальчиков был учтен два раза, в реальности Игорь, Паша и Володя могут покрасить забор за 14,4 часа=864 минуты.
Ответ: 864
1/18+1/20+1/30=50/360=5/36 забора.
Тем самым, они могли бы покрасить один забор за 7,2 часа. Поскольку каждый из мальчиков был учтен два раза, в реальности Игорь, Паша и Володя могут покрасить забор за 14,4 часа=864 минуты.
Ответ: 864
Слайд 6Задание№23: Функции и их свойства. Графики функций
Постройте график функции и определите,
при каких значениях прямая будет иметь с графиком единственную общую точку.
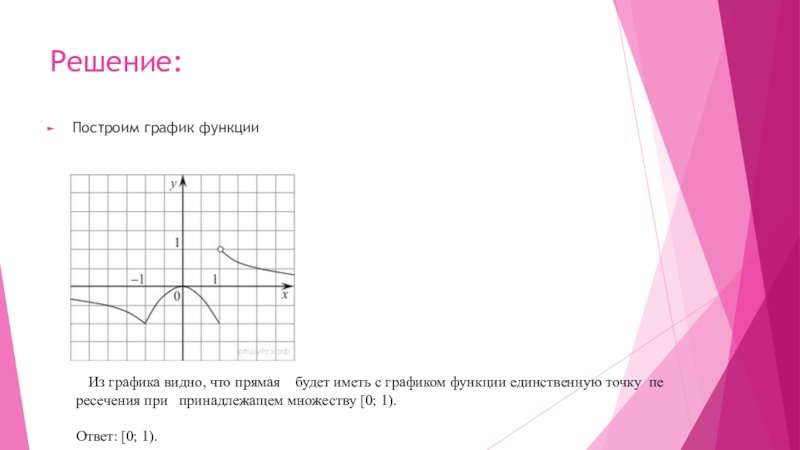
Слайд 7Решение:
Построим график функции
Из графика видно, что прямая будет иметь с графиком
функции единственную точку пересечения при принадлежащем множеству [0; 1).
Ответ: [0; 1).
Ответ: [0; 1).
Слайд 8Задание№24:Геометрическая задача на вычисление
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF = 24, BF = 10.
Слайд 9Решение:
Сумма углов, прилежащих к боковой стороне трапеции, равна 180° , значит,
Получаем,
что треугольник ABF прямоугольный с прямым углом F . По теореме Пифагора находим AB:
Ответ:26.
Ответ:26.
Слайд 10Задание№25: Геометрическая задача на доказательство
Три стороны параллелограмма равны. Докажите, что отрезок
с концами в серединах противоположных сторон параллелограмма равен четверти его периметра.
Слайд 11Решенеие:
В параллелограмме противоположные стороны равны, поэтому если равны три стороны, то
все стороны этого параллелограмма равны, значит, это ромб. Отрезки и равны и параллельны, следовательно, — параллелограмм, значит, длина равна длине стороны и, следовательно, равна четверти периметра параллелограмма.
Слайд 12Задание№26: Геометрическая задача повышенной сложности
Прямая, параллельная основаниям трапеции ABCD, пересекает её
боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD = 44, BC = 24, CF:DF = 3:1.
Слайд 13Решение:
Проведём построения и введём обозначения как показано на рисунке. Рассмотрим треугольники
KFC и ACD, угол C — общий, углы CAD и CKF равны друг другу как соответственные углы при параллельных прямых, следовательно, треугольники KFC и ACD подобны. Откуда
поэтому Аналогично, из треуголь
ников EKA и ABC получаем, что Таким образом,
Ответ:39.
поэтому Аналогично, из треуголь
ников EKA и ABC получаем, что Таким образом,
Ответ:39.