- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презентационный материал Расширение понятия числа
Содержание
- 1. Презентационный материал Расширение понятия числа
- 2. Рациональные числа.Понятие дроби. Обыкновенные дроби
- 3. Дробь-число, полученное в результате измерения величин (
- 4. Длина отрезка а может быть выражена бесконечным
- 5. Дроби, выражающие длину одного и того же
- 6. Теорема: для того, чтобы m/n была равна
- 7. Свойства дробей:Если числитель и знаменатель дроби умножить
- 8. Приведите дроби к наименьшему общему знаменателю:8/15 и 4/353/22 и 2/333/26 и 5/39
- 9. Правило 1 : Чтобы сравнить две дроби
- 10. Правило 2. Неправильная и смешанная дроби всегда
- 11. Правило 3. из двух смешанных дробей больше
- 12. Положительное рациональное число
- 13. Положительное рациональное число - множество равных дробей,
- 14. Положительные рациональные числа- числа, которые можно представить
- 15. Действия над положительными рациональными числами
- 16. Сложениеc=а+bЧтобы сложить два положительных рациональных числа a
- 17. Свойства:Коммуникативность: a+b=b+aАссоциативность: (a+b)+c=a+(b+c)Сократимость: a+c=b+ca=bМонотонность: a+b=a
- 18. Теоремы: У всякой неправильной дроби можно выделить
- 19. Вычитание положительных рациональных чисел a и b называется такое положительное рациональное число с, что a=b+c
- 20. Упражнения: Сложите дроби15/120+17/68+39/78311/12+53/15+12/9
- 21. 2. Сложите рациональным способом:2/15+15/13+31/5+43/26515/24+322/33+132/48+17/24+2/3
- 22. Найди разность:102/17-31/1357/36-19/54
- 23. Найди значение выражения:(7/8-4/5)+(1/20+1/4)-1/2(151/2-23/8)-(55/6+63/4)+(102/3-55/8)
- 24. Умножение и деление положительных рациональных чиселЕсли положительные
- 25. Запись положительных рациональных чисел в виде десятичных
- 26. Реши примеры:3,4+2,512,3-1,82,6*3,78,4:4
- 27. Бесконечные десятичные периодические дробиЕсли дробь m/n несократима
- 28. Запишите в виде обыкновенной дроби:0,(43)
- 29. ПроцентПроцент-это частный вид десятичных дробей, сотая доля
- 30. Процентное отношение первого числа ко второму, достаточно:1.Разделить
- 31. Чтобы найти указанное число процентов от данного
- 32. Нахождение числа, если известно несколько процентов этого
- 33. Отрицательные числа Отрицательное число-элемент множества отрицательных чисел,
- 34. Для каждого натурального числа n существует одно
- 35. .Вычитание целого числа а из другого целого числа b равносильно сложению b с противоположным для а:b-a=b+(-a)
- 36. Свойства отрицательных чисел :1. Если любое множество
- 37. Чтобы сложить два числа с разными знаками,
- 38. Понятие положительного иррационального числаИррациональные числа –это действительное
- 39. Слайд 39
Рациональные числа.Понятие дроби. Обыкновенные дроби
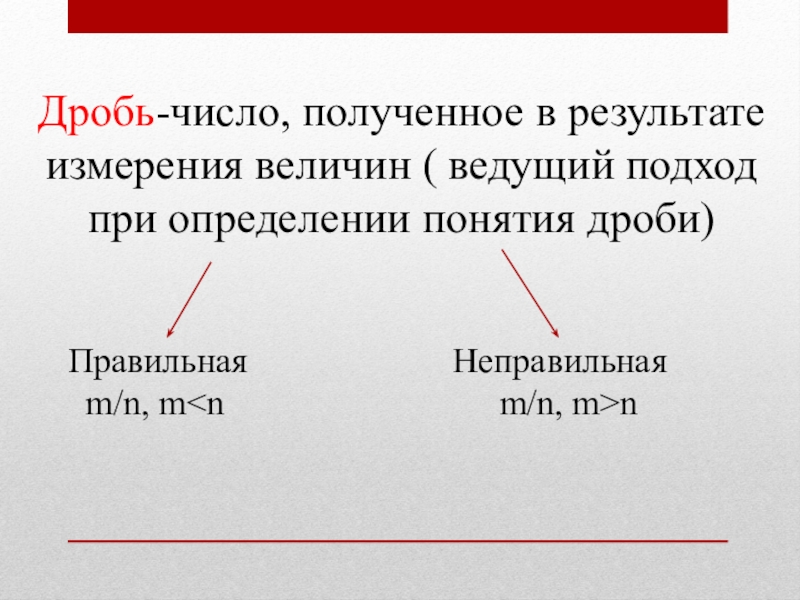
Слайд 3Дробь-число, полученное в результате измерения величин ( ведущий подход при определении
понятия дроби)
Правильная Неправильная
m/n, m
Слайд 4Длина отрезка а может быть выражена бесконечным множеством различных дробей, т.е
если при единице длины е длина отрезка а может быть выражена как m/n, то она может быть выражена любой дробью вида mk/nk, где k- натуральное число.
Слайд 5Дроби, выражающие длину одного и того же отрезка при единице длины
е, называют равными дробями. Если дроби m/n и p/q равны, то пишут m/n=p/q
Например: 14/4 и 28/8 выражают длину одного и того же отрезка при единице длины е, следовательно, 14/4=28/8
Например: 14/4 и 28/8 выражают длину одного и того же отрезка при единице длины е, следовательно, 14/4=28/8
Слайд 6Теорема: для того, чтобы m/n была равна дроби p/q, необходимо и
достаточно, чтобы mq=np
Равны ли дроби:
17/19 и 23/27
7/8 и 72/108
Равны ли дроби:
17/19 и 23/27
7/8 и 72/108
Слайд 7Свойства дробей:
Если числитель и знаменатель дроби умножить или разделить на одно
и то же натуральное число, то получится дробь, равная данной
Если числитель и знаменатель дроби являются взаимнопростыми, то дробь называется несократимой
Общий знаменатель двух дробей m/n и p/q, является любое общее кратное чисел n и q
Если числитель и знаменатель дроби являются взаимнопростыми, то дробь называется несократимой
Общий знаменатель двух дробей m/n и p/q, является любое общее кратное чисел n и q
Слайд 9Правило 1 : Чтобы сравнить две дроби с одинаковыми знаменателями, надо
сравнить их числители. Больше (меньше) та дробь, у которой числитель больше (меньше).
m/n>p/n, если m>p
Сравни дроби:
5/17 и 7/17
m/n>p/n, если m>p
Сравни дроби:
5/17 и 7/17
Слайд 10Правило 2. Неправильная и смешанная дроби всегда больше любой правильной дроби.
Правильная
дробь по определению меньше 1, поэтому неправильная и смешанная дробь
( имеющие в составе число, равное или больше 1) больше правильной дроби.
Сравни дроби:
21/3 и 8/15
7/3 и 7/8
( имеющие в составе число, равное или больше 1) больше правильной дроби.
Сравни дроби:
21/3 и 8/15
7/3 и 7/8
Слайд 11Правило 3. из двух смешанных дробей больше (меньше) та, у которой
целая часть дроби больше (меньше). При равенстве целых частей смешанных дробей больше (меньше) та дробь, у которой больше (меньше) дробная часть.
Слайд 13Положительное рациональное число - множество равных дробей, а каждая дробь, принадлежащая
этому множеству, и есть запись (представление) этого числа
Например:
Множество {4/3, 8/6, 12/9, 16/12…} есть некоторое положительное рациональное число, а дроби 4/3, 8/6, 12/9, 16/12-это различные записи этого числа.
Например:
Множество {4/3, 8/6, 12/9, 16/12…} есть некоторое положительное рациональное число, а дроби 4/3, 8/6, 12/9, 16/12-это различные записи этого числа.
Слайд 14Положительные рациональные числа- числа, которые можно представить в виде обыкновенных дробей
Q+
N
Множество
положительных рациональных чисел обозначают Q+ . Все натуральные числа содержатся в множестве положительных рациональных чисел N принадлежит Q+. Любое натуральное число можно представить в виде дроби.
Слайд 16Сложение
c=а+b
Чтобы сложить два положительных рациональных числа a и b нужно представить
их дробями с одинаковыми знаменателям и сложить их, оставив знаменатели теми же.
Слайд 17Свойства:
Коммуникативность: a+b=b+a
Ассоциативность: (a+b)+c=a+(b+c)
Сократимость: a+c=b+ca=b
Монотонность: a+b=a
Слайд 18Теоремы:
У всякой неправильной дроби можно выделить целую часть.
Всякую смешанную дробь
можно представить в виде неправильно дроби.
Слайд 19Вычитание положительных рациональных чисел a и b называется такое положительное рациональное
число с, что a=b+c
Слайд 24Умножение и деление положительных рациональных чисел
Если положительные рациональные числа выражены дробями
m/n и p/q, то их произведение представляется дробью:
m/n*p/q=mp/nq
Частное представляется дробью:
m/n:p/q=mq/np
m/n*p/q=mp/nq
Частное представляется дробью:
m/n:p/q=mq/np
Слайд 25Запись положительных рациональных чисел в виде десятичных дробей
Для того, чтобы несократимая
дробь m/n была равна десятичной дроби, необходимо и достаточно чтобы в разложении ее знаменателя на простые множители входили лишь числа 2 или 5
Слайд 27Бесконечные десятичные периодические дроби
Если дробь m/n несократима и в разложении знаменателя
есть простой множитель, отличный от 2 и 5, то дробь m/n представляется бесконечной десятичной периодической дробью
Последовательность повторяющихся после запятой в десятичной записи числа называется периодом. 6/7=0,857142857 (чисто периодическая дробь, где период начинается сразу после запятой)
3,27(346)(смешанная периодическая дробь)
Слайд 29Процент
Процент-это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу.
Например:
7% можно записать 7/100 или 0,07
Слайд 30Процентное отношение первого числа ко второму, достаточно:
1.Разделить первое число на второе
2.
Умножить полученное частное на 100 и на 0,01, передав последний множитель в виде знака %
Например:
Куриное яйцо весит 60 г, а его скорлупа 3 г. Найди процентное соотношение веса скорлупы к весу всего яйца
Например:
Куриное яйцо весит 60 г, а его скорлупа 3 г. Найди процентное соотношение веса скорлупы к весу всего яйца
Слайд 31Чтобы найти указанное число процентов от данного числа, достаточно умножит данное
число на сотую долю указанного числа процентов или, разделив заданное число на 100 (узнается 1 % от нео), умножить полученное частное на указанное число процентов (узнается все заданное число процентов от него))
Нахождение указанного числа процентов от данного числа
Слайд 32Нахождение числа, если известно несколько процентов этого числа
Чтобы найти число, зная,
чему равно от него несколько процентов, достаточно разделить это известное число на число указанных процентов, умножить полученное частное на 100
Найди:
20% от числа 15
30% от 700
Слайд 33Отрицательные числа
Отрицательное число-элемент множества отрицательных чисел, которое (вместе с нулем)
появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество целых чисел, состоящих из положительных натуральных чисел, отрицательных и нуля.
На числовой оси отрицательные числа располагаются левее нуля.
На числовой оси отрицательные числа располагаются левее нуля.
Слайд 34Для каждого натурального числа n существует одно и только одно отрицательное
число, обозначаемое – n, которое дополняет n до нуля
n+ (-n)=0
n+ (-n)=0
Оба числа называются противоположными друг для друга
Слайд 35.
Вычитание целого числа а из другого целого числа b равносильно сложению
b с противоположным для а:
b-a=b+(-a)
b-a=b+(-a)
Слайд 36Свойства отрицательных чисел :
1. Если любое множество положительных чисел ограничено снизу,
то любое множество отрицательных чисел ограничено сверху.
2. Любое отрицательное число меньше любого положительного числа. Из двух отрицательных чисел меньше то, модуль которого больше. Нуль больше любого отрицательного числа.
3. Любое число от прибавления положительного числа увеличивается, а от прибавления отрицательного уменьшается. Сумма двух противоположных чисел равна нулю
2. Любое отрицательное число меньше любого положительного числа. Из двух отрицательных чисел меньше то, модуль которого больше. Нуль больше любого отрицательного числа.
3. Любое число от прибавления положительного числа увеличивается, а от прибавления отрицательного уменьшается. Сумма двух противоположных чисел равна нулю
Слайд 37Чтобы сложить два числа с разными знаками, надо:
Из большего модуля вычесть
меньший;
Поставить перед полученным числом знак того слагаемого, модуль которого больше.
6,1+(-4,2)=+(6,1-4,2)=1,9
Или
6,1+(-4,2)=6,1-4,2=1,9
Реши: 2,7+(-3,4)
Поставить перед полученным числом знак того слагаемого, модуль которого больше.
6,1+(-4,2)=+(6,1-4,2)=1,9
Или
6,1+(-4,2)=6,1-4,2=1,9
Реши: 2,7+(-3,4)
Слайд 38Понятие положительного иррационального числа
Иррациональные числа –это действительное число, которое не является
рациональным, то есть которое не может быть представленным в виде дроби m/n, где m-целое число, а n-натуральное число.
Иррациональные числа можно получить и при извлечении корней из некоторых рациональных чисел ( корень из 2,7..)
Множество положительных иррациональных чисел обозначают символом I+
Иррациональные числа можно получить и при извлечении корней из некоторых рациональных чисел ( корень из 2,7..)
Множество положительных иррациональных чисел обозначают символом I+
