- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презентации к урокам математики
Содержание
- 1. Презентации к урокам математики
- 2. Цели урока: Научиться применять интегрирование функций в
- 3. План урока. 1. Организационный момент. Постановка проблемы.2.
- 4. 1612 г. Австрия город Линц.
- 5. Иоганн Кеплер(1571 – 1630)«Новая стереометрия винных бочек», 1615 г.
- 6. Если функция f(x) непрерывна на промежутке I
- 7. Вычисление объёмов тел.1. Заключаем тело Т между
- 8. 6. Разбиваем [a;b] на n - равных
- 9. Задача 1.Найти объём наклонной треугольной призмы с
- 10. АЛГОРИТМ ВЫЧИСЛЕНИЯ ОБЪЁМОВ ГЕОМЕТРИЧЕСКИХ ТЕЛ С ПОМОЩЬЮ
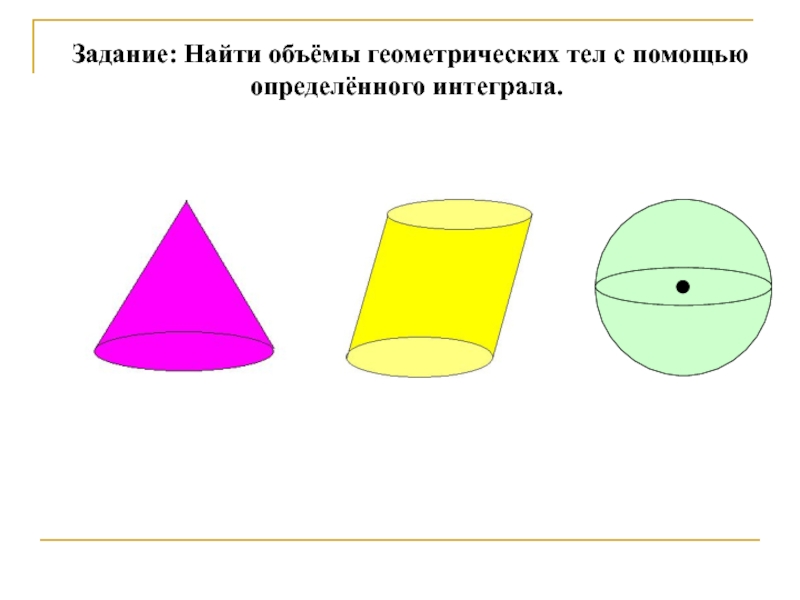
- 11. Задание: Найти объёмы геометрических тел с помощью определённого интеграла.
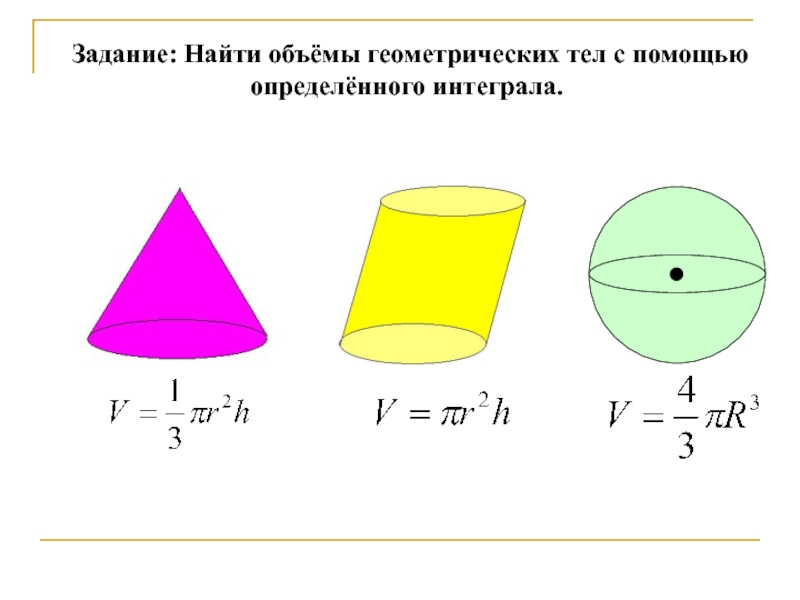
- 12. Задание: Найти объёмы геометрических тел с помощью определённого интеграла.
- 13. ДОМАШНЕЕ ЗАДАНИЕ. п 67-71, краткий конспект. Вывести
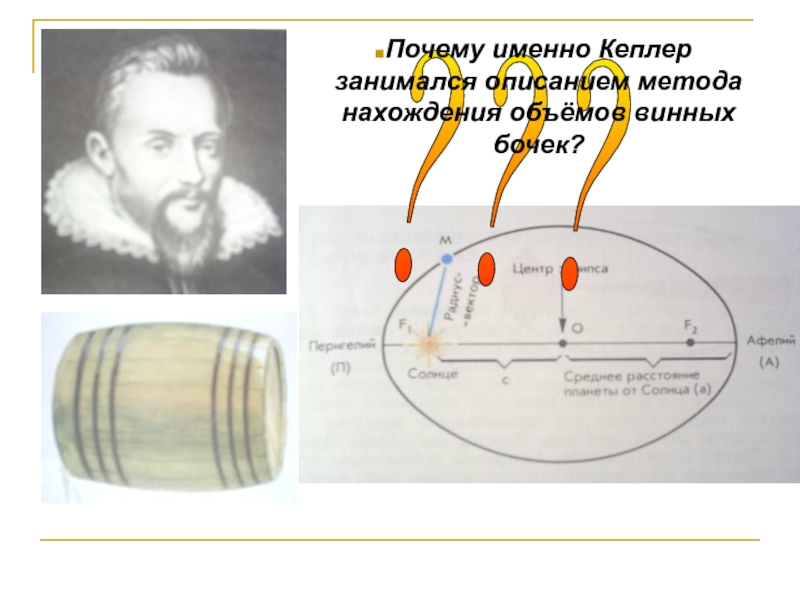
- 14. ???Почему именно Кеплер занимался описанием метода нахождения объёмов винных бочек?
- 15. Подведение итогов урокаМожно ли считать точным метод
Слайд 1Вычисление объемов геометрических тел с помощью определенного интеграла.
Чипышева Людмила Викторовна,
учитель математики
МОУ Гимназии №80
Слайд 2Цели урока:
Научиться применять интегрирование функций в качестве одного из способов решения
Развитие логического мышления, пространственного воображения, умений действовать по алгоритму, составлять алгоритмы действий.
Воспитание познавательной активности, самостоятельности.
Слайд 3План урока.
1. Организационный момент. Постановка проблемы.
2. Подготовка к восприятию материала: повторение
3. Изучение нового материала:
Раскрытие связи между двумя науками: алгеброй и геометрией. Вывод основной формулы для нахождения объёмов геометрических тел.
Коллективное решение задачи. Составление алгоритма действий.
Групповая работа. Решение задач на нахождение объёмов геометрических тел с помощью интеграла.
Защита решений и формулировка теорем.
4. Комментарии к домашнему заданию.
5. Итоги урока. Рефлексия.
Слайд 6Если функция f(x) непрерывна на промежутке I числовой оси, содержащей точки
формула Ньютона-Лейбница.
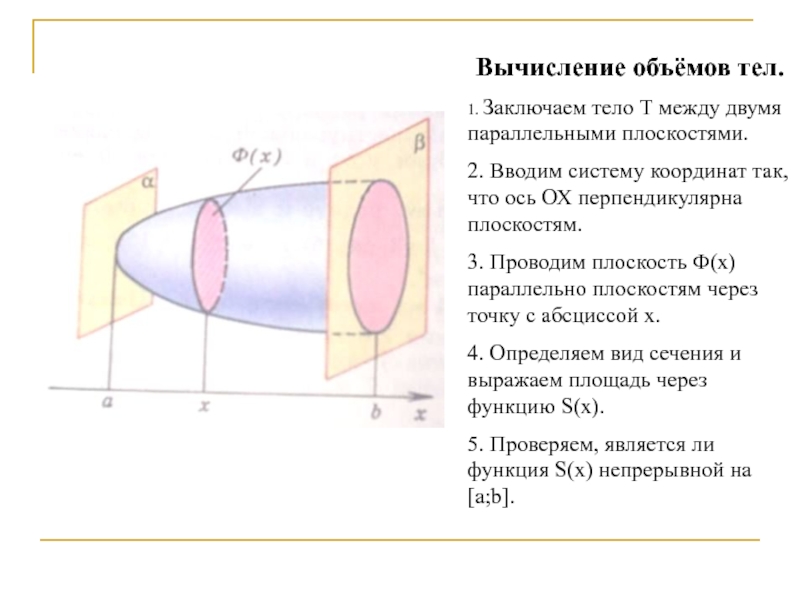
Слайд 7Вычисление объёмов тел.
1. Заключаем тело Т между двумя параллельными плоскостями.
2. Вводим
3. Проводим плоскость Ф(х) параллельно плоскостям через точку с абсциссой х.
4. Определяем вид сечения и выражаем площадь через функцию S(х).
5. Проверяем, является ли функция S(х) непрерывной на [a;b].
Слайд 86. Разбиваем [a;b] на n - равных отрезков точками а =
и проводим через хi плоскости перпендикулярно ОХ.
7. Плоскости разбивают тело Т на n- тел Т1, Т2, Т3,... Тn с основаниями Ф(хi) и высотой Δxi= (b - a)/n
8. V≈Vn= (S(x1) + S(x2) +…+ S(xn) )Δxi= =(S(x1) + S(x2) +…+ S(xn))(b - a)/n. При n →∞, Vn→V, поэтому
но 9.
Слайд 9Задача 1.Найти объём наклонной треугольной призмы с основанием S и высотой
1. Введём ось ОХ перпендикулярно основаниям призмы.
2. (АВС)∩OX=a, a=0, (A1B1C1) ∩ OX=b, b=h
3. Проведём плоскость перпендикулярно ОХ через точку с абсциссой х.
А2В2С2-треугольник, равный основаниям.
Площадь А2В2С2 равна S.
Ответ: V=Sh
4. S(x) непрерывна на [0;h]
Слайд 10АЛГОРИТМ ВЫЧИСЛЕНИЯ ОБЪЁМОВ ГЕОМЕТРИЧЕСКИХ ТЕЛ С ПОМОЩЬЮ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА.
1. Ввести систему
2. Найти пределы интегрирования а и b.
3. Провести сечение плоскостью перпендикулярно оси ОХ через точку с абсциссой х.
Определить вид сечения, задать формулой его площадь как функцию S(X).
4. Проверить непрерывность функции S(X) на [a;b].
5.
Слайд 13ДОМАШНЕЕ ЗАДАНИЕ.
п 67-71, краткий конспект.
Вывести формулу для нахождения объёма
Вывести формулу для нахождения объёма треугольной пирамиды с основанием S и высотой h.
Вывести формулу для нахождения объёма усечённой треугольной пирамиды с основаниями S1 и S2 и высотой h.
Слайд 15Подведение итогов урока
Можно ли считать точным метод Кеплера нахождения объёмов геометрических
Сравните его с методом, который узнали сегодня.
Спасибо за урок!






![Презентации к урокам математики 6. Разбиваем [a;b] на n - равных отрезков точками а = 6. Разбиваем [a;b] на n - равных отрезков точками а = х0, х1, х2, …хn=bи проводим через](/img/thumbs/125ebe82629ed7f9f73bd8e15370b4d4-800x.jpg)