Тема урока:
«Длина кружности».
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Прецентация по математике на тему Длина окружности (6 класс)
Содержание
- 1. Прецентация по математике на тему Длина окружности (6 класс)
- 2. Цели урока:Образовательныесистематизировать знания учащихся об окружности и
- 3. Задачи урока: – продолжить формирование навыков применения
- 4. Мы живём с братишкой дружно,Нам так весело
- 5. ОКРУЖНОСТЬ
- 6. Округлите число 3,1415926а) до десятитысячных;б) до тысячных;в)
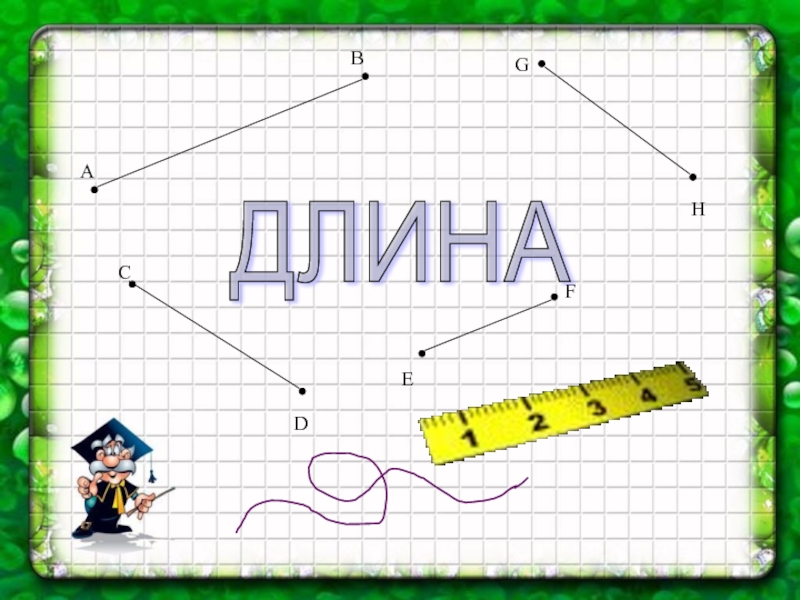
- 7. ABCDEFGHДЛИНА
- 8. Тема исследования: ДЛИНА ОКРУЖНОСТИ
- 9. ОАВСrrrОкружность – замкнутая линия, все точки которой
- 10. “Семь раз отмерь, один раз отрежь”Длина окружности обозначается буквой СОПЫТ №1
- 11. “Катилось колесо…”ОПЫТ №2
- 12. Слайд 12
- 13. Из истории числа πОбозначение числа «Пи» происходит
- 14. Число Архимедаπ ≈ 227
- 15. π = 3, 141592653589793238462643…
- 16. Запоминание числа π«Что я знаю о кругах»
- 17. Формулы длины окружностиC = πdC = 2πr
- 18. Задание №1Вычислить длину окружности С радиуса r,
- 19. Задание №2Вычислить длину окружности С, если:а). d
- 20. Задание №3Найдите радиус окружности, если её длина С = 25,12 см (π ≈ 3,14)
- 21. Задание №4Колесо, преодолев расстояние 188,4 метра, сделало 20 оборотов. Найдите диаметр колеса.
- 22. Тест1. Отрезок соединяющий центр окружности с точкой
- 23. Тест1. Отрезок соединяющий центр окружности с точкой
- 24. Итоги урокаПовторили пройденное…Узнали нового…Научились…
- 25. Домашнее заданиеп. 24 №868, №869Творческое задание
- 26. Спасибо за урок!
Цели урока:Образовательныесистематизировать знания учащихся об окружности и её элементах;ввести формулы для нахождения длины окружности по длине её диаметра и по длине её радиуса;продолжить формирование умения решать задачи на применение этих формул; Развивающиеразвитие графической культуры;развитие вычислительных навыков;обогащение
Слайд 1Учитель математики Косинец Е. В.
ГБОУ школа №106 Приморского района
Санкт-Петербурга.
Урок математики
6 класс
Слайд 2Цели урока:
Образовательные
систематизировать знания учащихся об окружности и её элементах;
ввести формулы для
нахождения длины окружности по длине её диаметра и по длине
её радиуса;
продолжить формирование умения решать задачи на применение этих формул;
Развивающие
развитие графической культуры;
развитие вычислительных навыков;
обогащение словарного запаса;
демонстрация меж предметных связей.
Воспитательные
продолжить формирование интереса к предмету;
продолжить формирование коммуникативной культуры учащихся;
её радиуса;
продолжить формирование умения решать задачи на применение этих формул;
Развивающие
развитие графической культуры;
развитие вычислительных навыков;
обогащение словарного запаса;
демонстрация меж предметных связей.
Воспитательные
продолжить формирование интереса к предмету;
продолжить формирование коммуникативной культуры учащихся;
Слайд 3Задачи урока:
– продолжить формирование навыков применения данных формул для нахождения длины
окружности;
–продолжить формирование умения применять свои знания на практике; работать самостоятельно и в паре;
– продолжить формирование познавательного интерес учащихся в ходе ознакомления с историческими сведениями;
– продолжить формирование навыков самостоятельной работы;
– продолжить формирование умения работать с имеющейся информацией;
–продолжить формирование умения применять свои знания на практике; работать самостоятельно и в паре;
– продолжить формирование познавательного интерес учащихся в ходе ознакомления с историческими сведениями;
– продолжить формирование навыков самостоятельной работы;
– продолжить формирование умения работать с имеющейся информацией;
Слайд 4Мы живём с братишкой дружно,
Нам так весело вдвоём,
Мы на лист поставим
кружку,
Обведём карандашом.
Получилось то, что нужно –
Называется…
Обведём карандашом.
Получилось то, что нужно –
Называется…
Слайд 6Округлите число 3,1415926
а) до десятитысячных;
б) до тысячных;
в) до сотых;
г) до десятых;
д)
до целых.
3,14 3,14159 3,1416 3 3,142 3,1
И К Д А Л Н
3,14 3,14159 3,1416 3 3,142 3,1
И К Д А Л Н
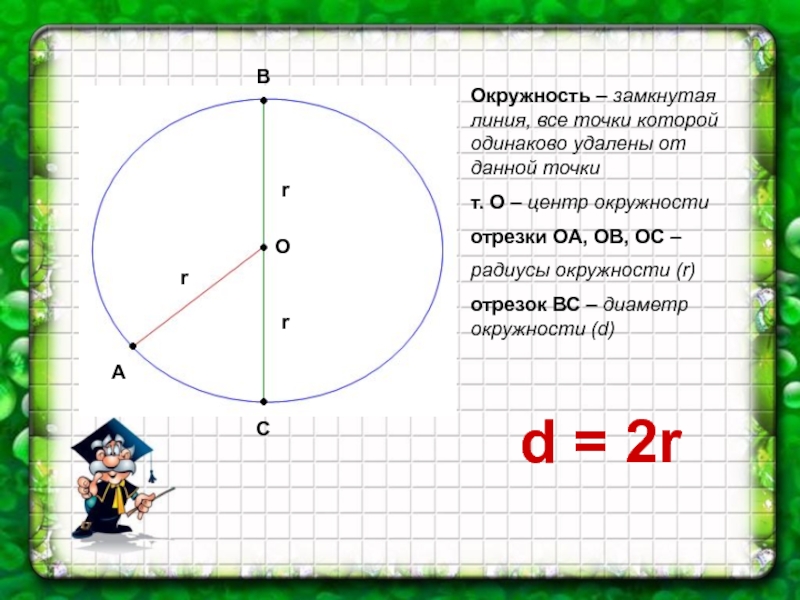
Слайд 9О
А
В
С
r
r
r
Окружность – замкнутая линия, все точки которой одинаково удалены от данной
точки
т. О – центр окружности
отрезки ОА, ОВ, ОС –
радиусы окружности (r)
отрезок ВС – диаметр окружности (d)
d = 2r
т. О – центр окружности
отрезки ОА, ОВ, ОС –
радиусы окружности (r)
отрезок ВС – диаметр окружности (d)
d = 2r
Слайд 13Из истории числа π
Обозначение числа «Пи» происходит от греческого слова perijerio
«периферия», что означает «окружность».
Впервые использовалось в 1706 году английский математик Уильям Джонс, но общепринятым оно стало после того, как его стал систематически употреблять Леонард Эйлер, начиная с 1736 года
Впервые использовалось в 1706 году английский математик Уильям Джонс, но общепринятым оно стало после того, как его стал систематически употреблять Леонард Эйлер, начиная с 1736 года
Слайд 16Запоминание числа π
«Что я знаю о кругах»
(количество букв в каждом
слове соответствует значению числа
π ≈ 3,1416)
π ≈ 3,1416)
Слайд 18Задание №1
Вычислить длину окружности С радиуса r, если:
a). r = 24
см; π ≈ 3,14
б). r = 4,7 дм; π ≈ 3,14
в). r = 1,54 м; π =
б). r = 4,7 дм; π ≈ 3,14
в). r = 1,54 м; π =
22
7
Слайд 21Задание №4
Колесо, преодолев расстояние 188,4 метра, сделало 20 оборотов. Найдите диаметр
колеса.
Слайд 22Тест
1. Отрезок соединяющий центр окружности с точкой на окружности называется:
1) диаметр
2) хорда 3) радиус 4) сторона
2. Чему равен диаметр окружности, если её радиус 4,7 м?
1) 8,14 2) 2,35 3) 9,4 4) 9,14
3. Число π приближенно равно:
1) 1,43 2) 3,14 3) 3,41 4) 4,13
4. Формула для вычисления длины окружности:
1) С = 2πd 2) C = 2πr 3) C = πr 4) C = 2d
5. Колесо преодолело расстояние 17, 5 м за пять оборотов. Длина окружности колеса:
1) 87,5 м 2) 3,5 м 3) 0,35 м 4) 35 м
2. Чему равен диаметр окружности, если её радиус 4,7 м?
1) 8,14 2) 2,35 3) 9,4 4) 9,14
3. Число π приближенно равно:
1) 1,43 2) 3,14 3) 3,41 4) 4,13
4. Формула для вычисления длины окружности:
1) С = 2πd 2) C = 2πr 3) C = πr 4) C = 2d
5. Колесо преодолело расстояние 17, 5 м за пять оборотов. Длина окружности колеса:
1) 87,5 м 2) 3,5 м 3) 0,35 м 4) 35 м
Слайд 23Тест
1. Отрезок соединяющий центр окружности с точкой на окружности называется:
1) диаметр
2) хорда 3) радиус 4) сторона
2. Чему равен диаметр окружности, если её радиус 4,7 м?
1) 8,14 2) 2,35 3) 9,4 4) 9,14
3. Число π приближенно равно:
1) 1,43 2) 3,14 3) 3,41 4) 4,13
4. Формула для вычисления длины окружности:
1) С = 2πd 2) C = 2πr 3) C = πr 4) C = 2d
5. Колесо преодолело расстояние 17, 5 м за пять оборотов. Длина окружности колеса:
1) 87,5 м 2) 3,5 м 3) 0,35 м 4) 35 м
2. Чему равен диаметр окружности, если её радиус 4,7 м?
1) 8,14 2) 2,35 3) 9,4 4) 9,14
3. Число π приближенно равно:
1) 1,43 2) 3,14 3) 3,41 4) 4,13
4. Формула для вычисления длины окружности:
1) С = 2πd 2) C = 2πr 3) C = πr 4) C = 2d
5. Колесо преодолело расстояние 17, 5 м за пять оборотов. Длина окружности колеса:
1) 87,5 м 2) 3,5 м 3) 0,35 м 4) 35 м