- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему практическое применение кубика Рубика
Содержание
- 1. практическое применение кубика Рубика
- 2. Развивает память, логическое мышление, пространственное воображение, моторику
- 3. Объект исследования: учащиеся 5-9 классов КГУ «Комплекс
- 4. Кубик Рубика: от создания до наших
- 5. Интересные фактыСамый большой кубик РубикаСамый маленький кубик РубикаСамый дорогой кубик Рубика
- 6. Методики сборки кубика Рубика:Грани кубика Рубика -
- 7. Математика кубика РубикаPn = n·(n−1)·(n−2) = n!
- 8. Соревнования по скоростной сборке: СпидкубингЛогика и системное
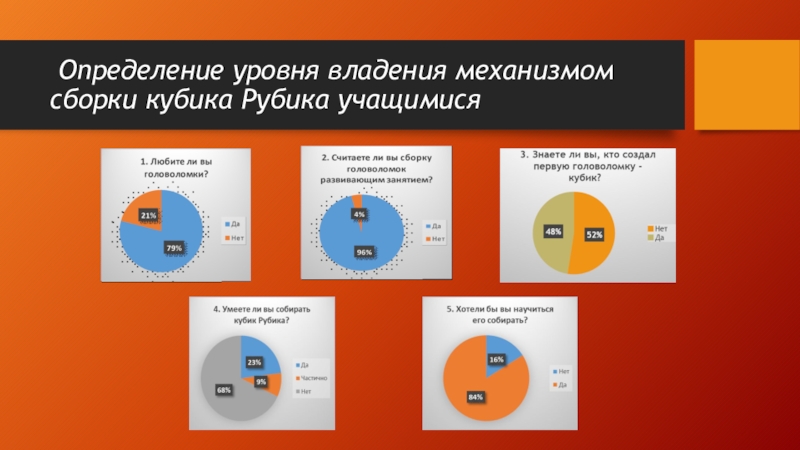
- 9. Определение уровня владения механизмом сборки кубика Рубика учащимися
- 10. Разработка алгоритма сборки кубика
- 11. Решение задач по математике с применением кубика
- 12. Определение уровня наглядно-действенного мышления дошкольника с
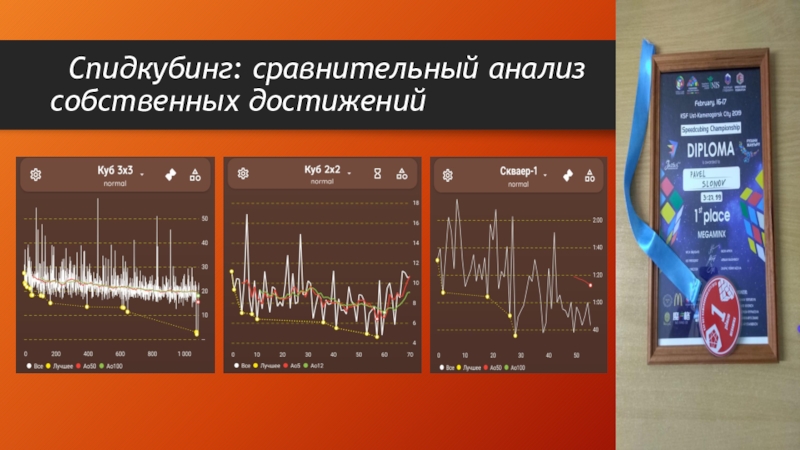
- 13. Спидкубинг: сравнительный анализ собственных достиженийМ
- 14. Слайд 14
Слайд 1ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ КУБИКА РУБИКА
Автор: ученик 7 класса КГУ «Комплекс
Руководитель: Зарубина Елена Витальевна, учитель математики
Слайд 2Развивает память, логическое мышление, пространственное воображение, моторику пальцев
Помогает осваивать предметы математического
Гипотеза: если освоить основные алгоритмы сборки кубика Рубика, то можно найти им практическое применение
Цель: выявление областей практического применения кубика Рубика
Задачи:
Изучить историю кубика Рубика - от создания до наших дней;
Выявить уровень владения механизмом сборки учащимися;
Составить основные алгоритмы сборки кубика Рубика;
Отобрать математические задачи, в основу решения которых можно положить алгоритм сборки кубика Рубика ;
Определить уровень наглядно-действенного мышления дошкольника с помощью кубика Рубика;
Проанализировать собственные результаты по сборке кубика Рубика;
Создать мастер-класс по сборке кубика Рубика.
АКТУАЛЬНОСТЬ
Слайд 3Объект исследования: учащиеся 5-9 классов КГУ «Комплекс Предгорненская средняя школа –
Предмет исследования: кубик Рубика.
Научная новизна исследования: создание видео «Мастер-класс по сборке кубика Рубика».
Практическая значимость: разработанные мною алгоритмы сборки различных модификаций кубика Рубика и видео могут быть полезными всем желающим научиться его собирать и решать математические задачи.
Материал и методика исследований. При работе над теоретической частью проекта я использовал описательный и исторический методы; практические исследования – по методам Д.Фридрих, М. Ростовикова, алгоритму Е.Бондаренко
Слайд 4 Кубик Рубика: от создания до наших дней
Родился в 1944 году
В настоящее время в основном участвует в разработке видеоигр, пишет статьи по архитектуре и возглавляет студию Рубика. Награждён Государственной премией Венгерской народной республики (1983), Премией им. Дэнниса Габора (1995) и Кошутовской премией (2007)
ЕРНЕ РУБИК
Слайд 5Интересные факты
Самый большой кубик Рубика
Самый маленький кубик Рубика
Самый дорогой кубик Рубика
Слайд 6Методики сборки кубика Рубика:
Грани кубика Рубика - 9 элементов, которые можно
Алгоритм Марвина Тистлетуэйта или"как поймать льва в пустыне" (метод половинного деления)
Алгоритм Коцембы:
точное значение числа Бога равно 20!
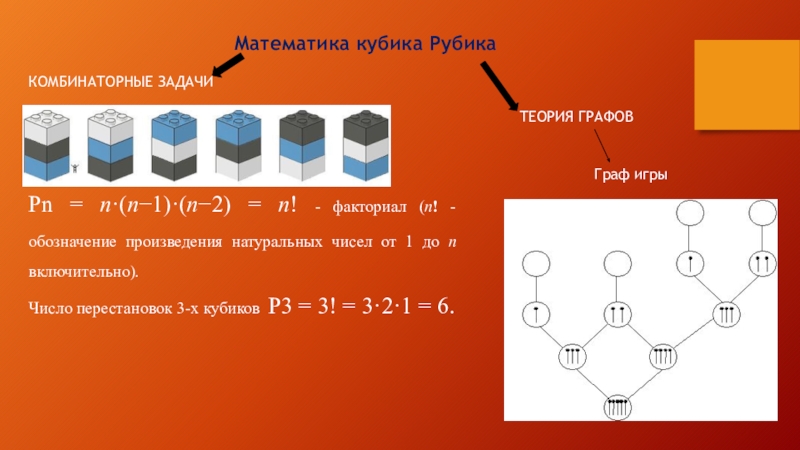
Слайд 7Математика кубика Рубика
Pn = n·(n−1)·(n−2) = n! - факториал (n! -
Число перестановок 3-х кубиков P3 = 3! = 3·2·1 = 6.
КОМБИНАТОРНЫЕ ЗАДАЧИ
ТЕОРИЯ ГРАФОВ
Граф игры
Слайд 8Соревнования по скоростной сборке: Спидкубинг
Логика и системное мышление
Быстрое понимание алгоритмов
Зрительная память
Ловкость
Наглядно – действенное и
пространственное мышление
Действующий рекорд по сборке кубика 3*3*3* - 4,74 сек (Матс Валк, голландский спидкубер, 2016)
Слайд 10 Разработка алгоритма сборки кубика модификации 3*3*3*
Шаг 1. "Правая
Шаг 3. "Глаза" Шаг 4. "Уши"
Шаг 5. Собранная сторона
Слайд 11Решение задач по математике с применением кубика Рубика
Можно ли нарисовать на
Куб, стоящий на плоскости, несколько раз перекатили через его рёбра, после чего он вернулся на прежнее место. Обязательно ли он стоит на той же грани? (Пусть куб находится перед нами, а нижняя грань окрашена. Рассмотрим следующий путь куба (см. рисунок). Ответ: нет.
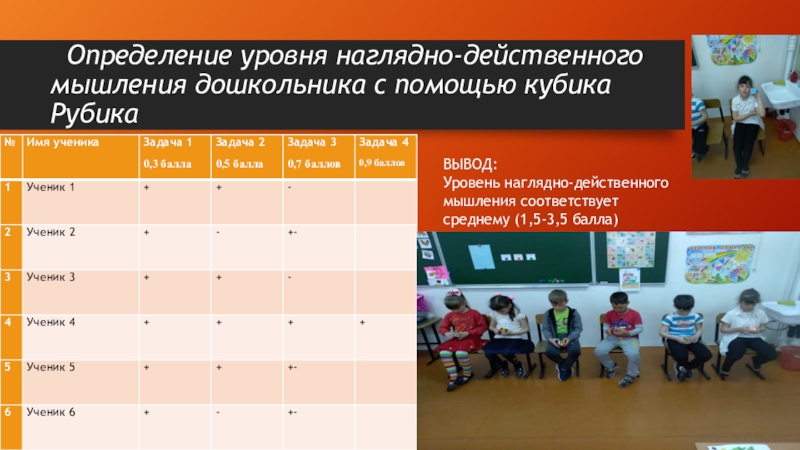
Слайд 12 Определение уровня наглядно-действенного мышления дошкольника с помощью кубика Рубика
ВЫВОД:
Уровень
Слайд 14
Алгоритмы сборки Кубика Рубика могут быть использованы при решении комбинаторных задач по математике.
Теория графов применяется в транспортных и коммуникационных системах (для составления оптимальных маршрутов доставки грузов или маршрутизации данных в Интернете)
Увлечение спидкубингом развивает навыки и компетенции, столь необходимые подростку в современном мире
С помощью заданий по сборке кубика Рубика можно определить уровень наглядно-действенного мышления для диагностики подготовленности ребенка к школе
Разработав программу курса, в рамках кружка «Юный математик» в следующем учебном году возможно проведение мастер-классов по сборке кубика Рубика