- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Подготовка к ЕГЭ Теория вероятностей
Содержание
- 1. Подготовка к ЕГЭ Теория вероятностей
- 2. Задача 1. На экзамене 40 вопросов, Коля
- 3. Задача 2. В фирме такси в данный
- 4. Задача 3. В случайном эксперименте бросают три
- 5. Задача 4. В случайном эксперименте симметричную монету
- 6. Задача 5. Научная конференция проводится в 3
- 7. Задача 6. Перед началом первого тура чемпионата
- 8. Задача 7. В чемпионате мира участвуют 20
- 9. Задача 8. На клавиатуре телефона 10 цифр,
- 10. Задача 9. Какова вероятность того, что случайно
- 11. Задача 10. В классе 21 учащийся, среди
- 12. Задача 11. Вероятность того, что новый блендер
- 13. Задача 12. Механические часы с двенадцатичасовым циферблатом
- 14. Задача 13. Фабрика выпускает сумки. В среднем
- 15. Задача 14. Две фабрики выпускают одинаковые стекла
- 16. Задача 15. Помещение освещается фонарём с двумя
- 17. Задача 16. В случайном эксперименте симметричную монету
- 18. Задача 17 В случайном эксперименте бросают три
- 19. Задача 18. Если гроссмейстер А. играет белыми,
- 20. Задача 19. В торговом центре два одинаковых
- 21. Задача20: Биатлонист пять раз стреляет по мишеням.
Слайд 1Подготовка к ЕГЭ
(профильный уровень)
Задание 5
Математика 11
МБОУ СОШ «Солнечная» Дмитровская Елена
Слайд 2Задача 1. На экзамене 40 вопросов, Коля не выучил 4 из
Слайд 3Задача 2. В фирме такси в данный момент свободно 35 машин:
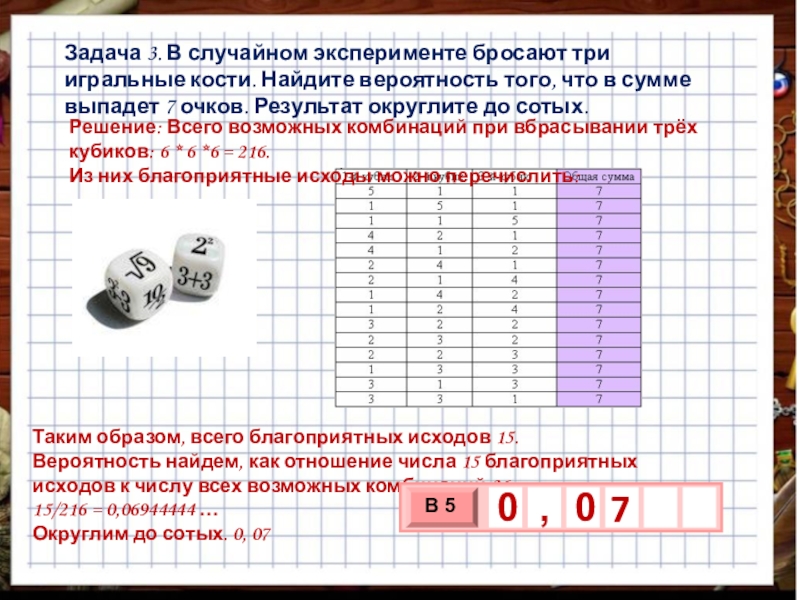
Слайд 4Задача 3. В случайном эксперименте бросают три игральные кости. Найдите вероятность
Решение: Всего возможных комбинаций при вбрасывании трёх кубиков: 6 * 6 *6 = 216.
Из них благоприятные исходы можно перечислить:
Таким образом, всего благоприятных исходов 15.
Вероятность найдем, как отношение числа 15 благоприятных исходов к числу всех возможных комбинаций 36.
15/216 = 0,06944444 …
Округлим до сотых. 0, 07
Слайд 5Задача 4. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность
Решение:
Благоприятный исход: орел – орел – орел - орел.
Всего исходов : 2 · 2 · 2 · 2 = 16.
Значит, вероятность того, что решка не выпадет ни разу – есть 1/16 = 0,0625.
Слайд 6Задача 5. Научная конференция проводится в 3 дня. Всего запланировано 75
Решение:
Всего запланировано 75 докладов, и так как в первый день запланировано 27, то на оставшиеся два дня остается 75 – 27 = 48 докладов, при этом во второй и третий дни будет прочитано по 48 :2 = 24 доклада.
Значит вероятность, что доклад профессора М. окажется запланированным на третий день есть 24/75 = 8/25 = 0,32;
Слайд 7Задача 6. Перед началом первого тура чемпионата по шашкам участников разбивают
Решение:
В первом туре Василий Лукин может сыграть с 26 − 1 = 25 шашистом, из которых 3 − 1 = 2 из России.
Значит, вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России, есть 2/25 = 0,08;
Слайд 8Задача 7. В чемпионате мира участвуют 20 команд. С помощью жребия
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда Китая окажется в первой группе?
Решение:
Количество карточек с номером «1» – 4 штуки. Всего карточек (команд) – 20.
Значит, вероятность того, что команда Китая окажется в первой группе равна
4/20 = 1/5 = 0,2;
Слайд 9Задача 8. На клавиатуре телефона 10 цифр, от 0 до 9.
Решение:
На клавиатуре телефона цифр меньше 4-х – 4 штуки (0; 1; 2; 3). Всего цифр 10.
Значит, вероятность того, что случайно нажатая цифра будет меньше 4 равна 4/10 = 0,4;
Слайд 10Задача 9. Какова вероятность того, что случайно выбранное натуральное число от
Решение:
От 41 до 56 ровно 16 чисел. Среди них четных 8 штук (42; 44; 46; 48; 50; 52; 54; 56).
Значит, вероятность того, что случайно выбранное натуральное число от 41 до 56 делится на 2 равна
8/16 = 0,5;
Слайд 11Задача 10. В классе 21 учащийся, среди них два друга — Вадим
Решение:
Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 6 человек из 20 оставшихся учащихся. Вероятность того, что друг окажется среди этих 6 человек, равна 6 : 20 = 0,3.
Слайд 12Задача 11. Вероятность того, что новый блендер в течение года поступит
Решение:
Частота события «гарантийный ремонт» составляет 102 : 1000 = 0,102.
Вероятность же, что новый блендер в течение года поступит в гарантийный ремонт, равна 0,096.
Разница между частотой события и вероятностью составляет 0,102 - 0,096 = 0,006.
Слайд 13Задача 12. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались
Решение:
На циферблате между 6 часами и 9 располагаются три часовых деления.
Всего на циферблате 12 часовых делений. Поэтому искомая вероятность равна:
3 :12 = 0,25;
Слайд 14Задача 13. Фабрика выпускает сумки. В среднем на 160 качественных сумок
Слайд 15Задача 14. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая
Решение.
Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,45 · 0,03 = 0,0135.
Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,55 · 0,01 = 0,0055.
Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна 0,0135 + 0,0055 = 0,019.
Слайд 16Задача 15. Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы
Решение.
Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,3 · 0,3 = 0,09.
Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна 1 − 0,09 = 0,91.
Слайд 17Задача 16. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность
Решение: Всего возможных 2³ = 8 вариантов: ООО, ООР, ОРО, РОО,ОРР, РОР, РРО, РРР; значит m = 8
Благоприятных 3: n = 3
Вероятность равна Р = 3/8 = 0,375.
Слайд 18Задача 17 В случайном эксперименте бросают три игральные кости. Найдите вероятность
Решение: Всего вариантов выпадения для трёх кубиков m= 6³ = 216 (каждый из кубиков имеет 6 граней).
А подходящих для нас (сумма равна 16) всего n = 6:
16 = 6+6+4 = 6+4+6 = 4+6+6 = 5+5+6 = 5+6+5 = 6+5+5.
Искомая вероятность равна Р = 6/216 = ¹⁄₃₆ ≈ 0,03.
Слайд 19Задача 18. Если гроссмейстер А. играет белыми, то он выигрывает у
Решение.
Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,52 · 0,3 = 0,156.
Слайд 20Задача 19. В торговом центре два одинаковых автомата продают кофе. Вероятность
Решение: Рассмотрим события .А = кофе закончится в первом автомате,
В = кофе закончится во втором автомате. Тогда
A•B = кофе закончится в обоих автоматах, A + B = кофе закончится хотя бы в одном автомате.
По условию P(A) = P(B) = 0,3; P(A•B) = 0,12.
События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
P(A + B) = P(A) + P(B) − P(A•B) = 0,3 + 0,3 − 0,12 = 0,48.
Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1 − 0,48 = 0,52.
Слайд 21Задача20: Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень
Решение: Результат каждого следующего выстрела не зависит от предыдущих. Поэтому события «попал при первом выстреле», «попал при втором выстреле» и т.д. независимы.
Вероятность каждого попадания равна 0,8. Значит, вероятность промаха равна 1 – 0,8 = 0,2.
1 выстрел: Р= 0,8 ; 2 выстрел : Р= 0,8 ; 3 выстрел : Р= 0,8;
4 выстрел :Р = 0,2 ;5 выстрел :Р= 0,2
По формуле умножения вероятностей независимых событий, получаем, что искомая вероятность равна:
Р=0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02.