- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Подготовка к ЕГЭ. Решение зад.С2.С4
Содержание
- 1. Подготовка к ЕГЭ. Решение зад.С2.С4
- 2. 1. Опорные знания:Теорема синусов; Теорема косинусов;Угол между
- 3. 2. Решение задач по готовым рисункам: DACBS1.)
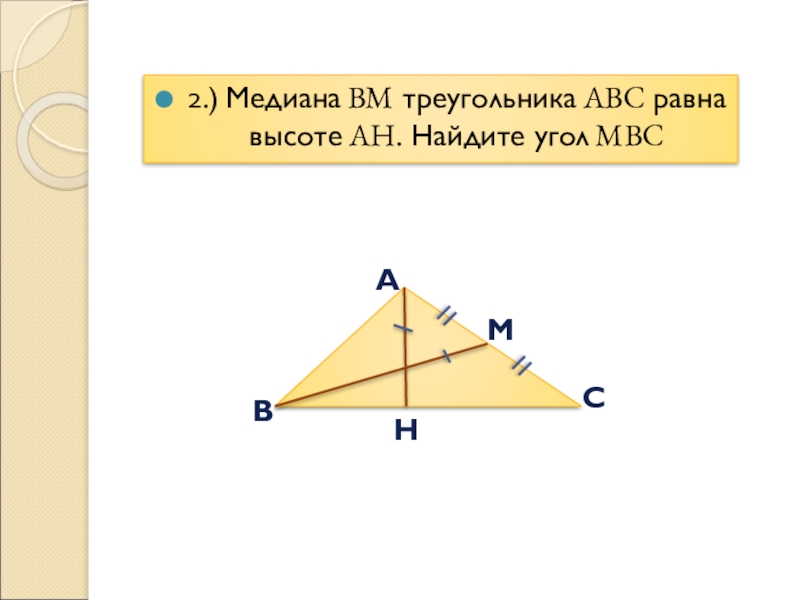
- 4. ABCMH2.) Медиана BM треугольника ABC равна высоте AH. Найдите угол MBC
- 5. 3.) В кубе ABCDA1B2C3D4 E - середина
- 6. 3. Решение задач :1.) В треугольнике ABC
- 7. 1.) В треугольнике ABC угол A равен
- 8. 3.) Ребра AD и BC
- 9. 3.) Ребра AD и BC пирамиды DABC
- 10. 3.) Около трапеции ABCD описана окружность радиуса
- 11. 3.) Около трапеции ABCD описана окружность радиуса
- 12. 2.) В правильной шестиугольной призме A..F1 ,
- 13. 5.) В кубе ABCDA1B2C3D4 E - середина
1. Опорные знания:Теорема синусов; Теорема косинусов;Угол между двумя прямыми;Угол между прямой и плоскостью;Угол между двумя плоскостямиСтороны правильного шестиугольника и треугольника вписанного в окружность.
Слайд 1Дзбоева ТБ,
учитель математики МБОУСОШ №2
г.Алагира РСО-А.
Подготовка к ЕГЭ
(решение заданий С2,С4)
Слайд 21. Опорные знания:
Теорема синусов;
Теорема косинусов;
Угол между двумя прямыми;
Угол между прямой
и плоскостью;
Угол между двумя плоскостями
Стороны правильного шестиугольника и треугольника вписанного в окружность.
Угол между двумя плоскостями
Стороны правильного шестиугольника и треугольника вписанного в окружность.
Слайд 32. Решение задач
по готовым рисункам:
D
A
C
B
S
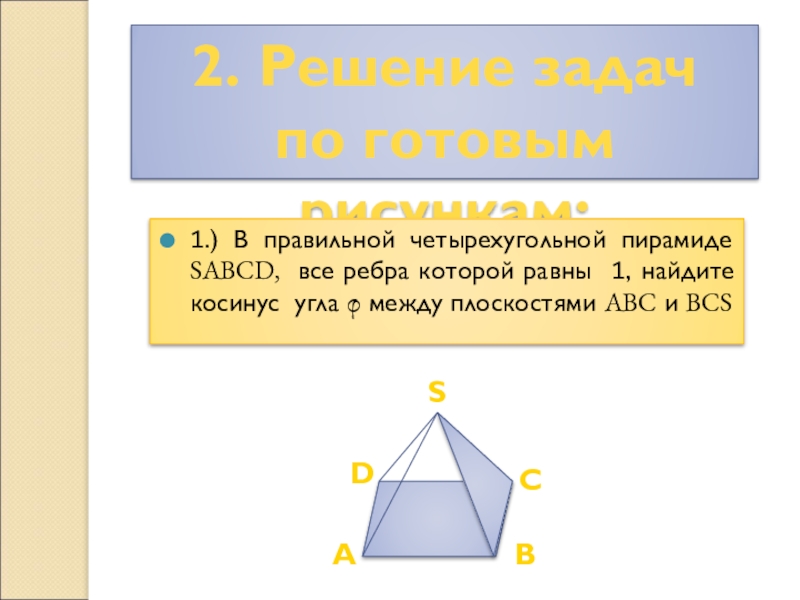
1.) В правильной четырехугольной пирамиде
SABCD, все ребра которой равны 1, найдите косинус угла φ между плоскостями ABC и BCS
Слайд 5
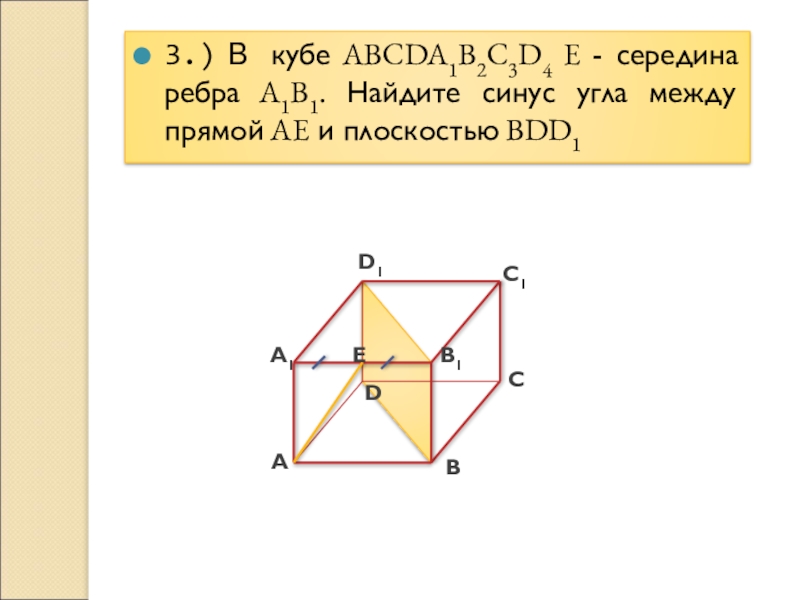
3.) В кубе ABCDA1B2C3D4 E - середина ребра A1B1. Найдите синус
угла между прямой AE и плоскостью BDD1
A
B
C
E
A1
B1
C1
D1
D
Слайд 63. Решение задач :
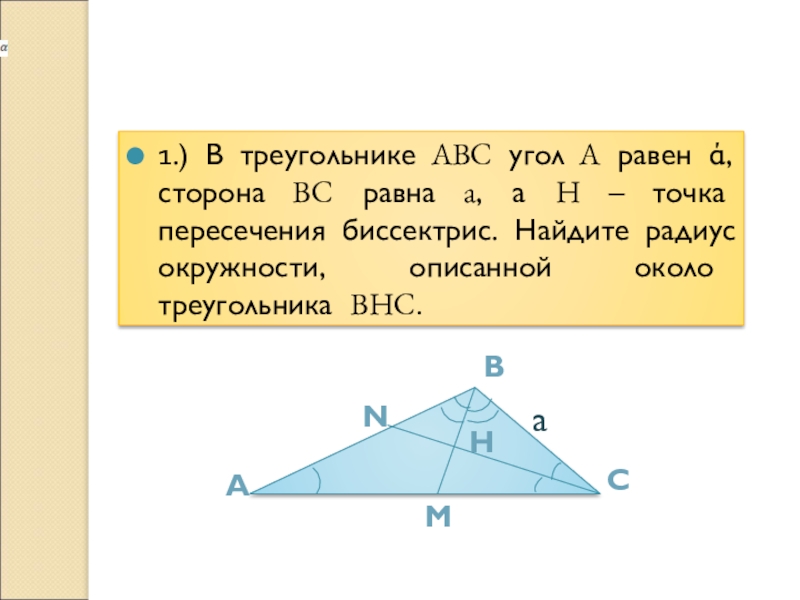
1.) В треугольнике ABC угол A равен ά,
сторона BC равна a, а H – точка пересечения биссектрис. Найдите радиус окружности, описанной около треугольника BHC.
Слайд 71.) В треугольнике ABC угол A равен ά, сторона BC равна
a, а H – точка пересечения биссектрис. Найдите радиус окружности, описанной около треугольника BHC.
A
B
C
N
M
H
a
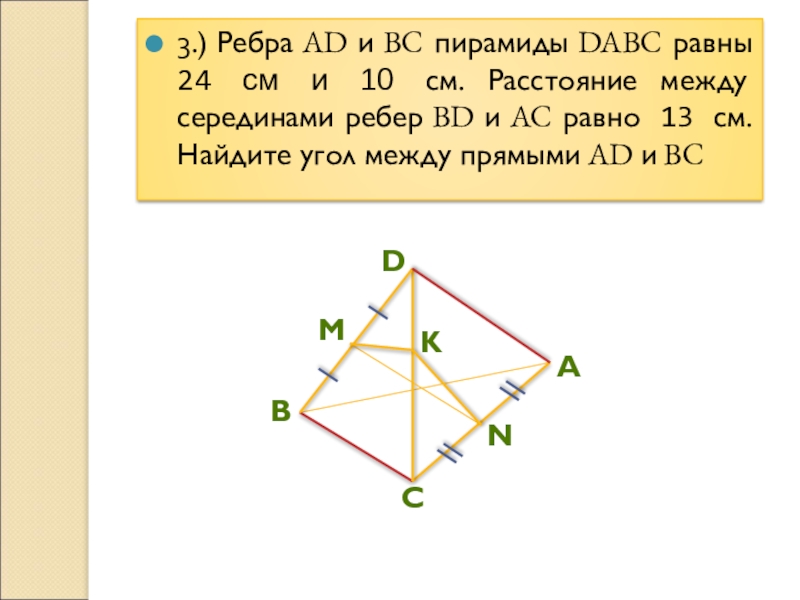
Слайд 8 3.) Ребра AD и BC пирамиды DABC равны 24 см и
10 см. Расстояние между серединами ребер BD и AC равно 13 см. Найдите угол между прямыми AD и BC
Слайд 93.) Ребра AD и BC пирамиды DABC равны 24 см и
10 см. Расстояние между серединами ребер BD и AC равно 13 см. Найдите угол между прямыми AD и BC
A
D
N
C
B
M
K
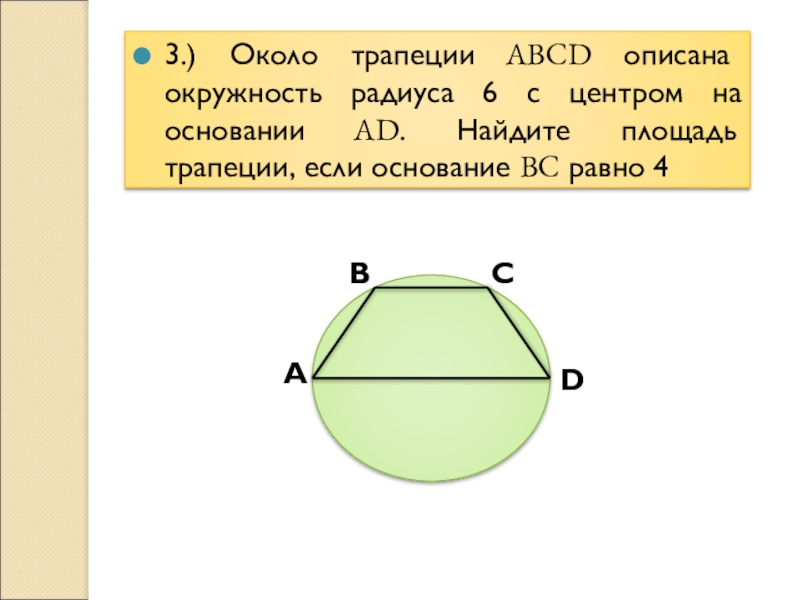
Слайд 103.) Около трапеции ABCD описана окружность радиуса 6 с центром на
основании AD. Найдите площадь трапеции, если основание BC равно 4
Слайд 113.) Около трапеции ABCD описана окружность радиуса 6 с центром на
основании AD. Найдите площадь трапеции, если основание BC равно 4
A
B
C
D
Слайд 12
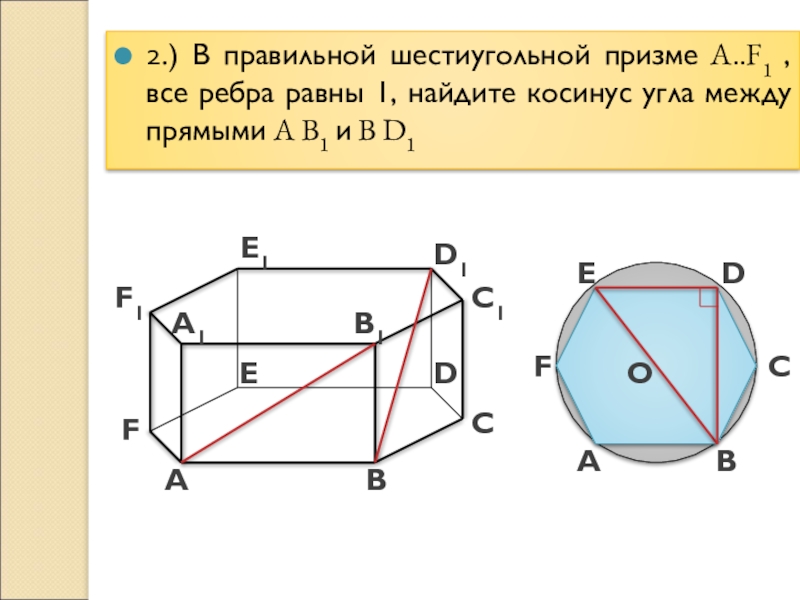
2.) В правильной шестиугольной призме A..F1 , все ребра равны 1,
найдите косинус угла между прямыми A B1 и B D1
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
O
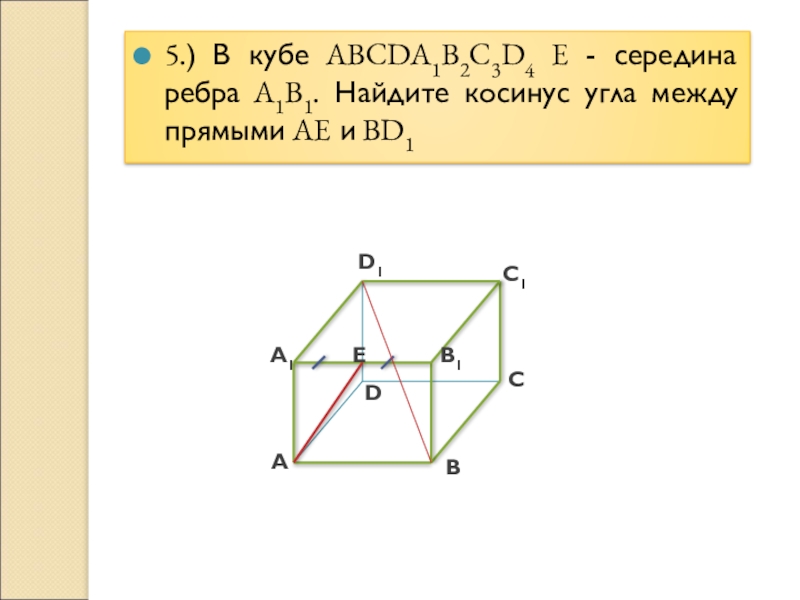
Слайд 135.) В кубе ABCDA1B2C3D4 E - середина ребра A1B1. Найдите косинус
угла между прямыми AE и BD1
A
B
C
E
A1
B1
C1
D1
D