- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему По теме Основные понятия теории вероятности и математической статистики
Содержание
- 1. По теме Основные понятия теории вероятности и математической статистики
- 2. получение базовых знаний и формирование основных навыков
- 3. научиться вычислять вероятности события; вероятности событий по
- 4. Людей всегда интересовало будущее. Человечество во все времена
- 5. Вероятность - возможность исполнения, осуществимости чего -
- 6. Комбинаторика — наука о составлении и подсчете комбинаций.
- 7. Действия с числамисложениеВычитаниеумножениеделение
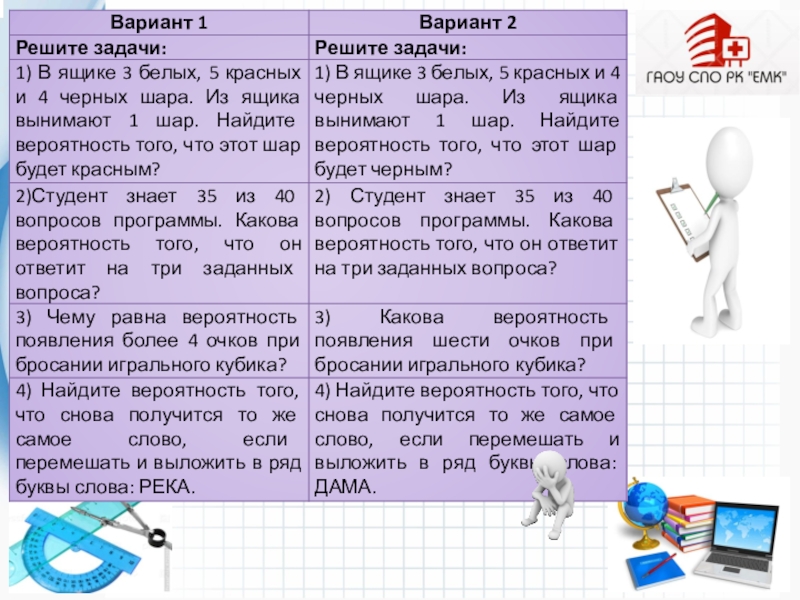
- 8. Задания
- 9. Ответы:
- 10. 0 ошибок – «5»1 ошибка – «4»2
- 11. Скульптура Михаила Шемякина «Дети - жертвы пороков взрослых»
- 12. наркомания
- 13. проституция
- 14. воровство
- 15. алкоголизм
- 16. невежество
- 17. лженаучность
- 18. равнодушие
- 19. пропаганда насилия
- 20. садизм
- 21. для беспамятных
- 22. эксплуатация детского труда
- 23. нищета
- 24. образ войны
- 25. «Приобщение к азартным играм»
- 26. «Играть или не играть?»
- 27. Теоретический опрос1.Дайте определения основным понятиям теории вероятности:
- 28. Проверка домашнего задания
- 29. Слайд 29
- 30. 0-1 ошибка – «5»;2 ошибки – «4»;3
- 31. Изучая понятие «вероятности», существует довольно широкий круг
- 32. Алгоритм решения задач на расчет вероятности по
- 33. Вероятность любого события не может быть меньше
- 34. Решение задачЗадача №1. Если организаторы лотереи выпустили
- 35. Решение: по формуле классической вероятности нам известно
- 36. Задача №2. В больнице берутся десять историй
- 37. Решение: Обозначим через А – событие, которое
- 38. Задача №3. На книжной полке находятся 2
- 39. Решение: Обозначим через А – событие которое
- 40. Задача №4. В коробке находится 15 медицинских
- 41. Решение: Обозначим через А событие, которое состоит
- 42. Задача №5. Из 60 вопросов студент подготовил
- 43. Решение: Событие А – студент сдаст экзамен.Ответ: 69%.
- 44. «Простейший пример неоднозначной задачи: если подбросить монету,
- 45. исторические фактыЖорж Бюссон (1707-1788) бросал монету 4040 раз, и «орел» выпал в 2048 случаях.
- 46. Чарльз Пирсон (1857-1936) 24000 раз подбросил монету, «орел» выпал 12012 раз.
- 47. Какие из следующих событий – случайные, достоверные,
- 48. Придумайте и запишите в тетрадь события, чтобы они соответствовали знакам в таблице.
- 49. Задача №6. Найти вероятность выигрыша в лотерее
- 50. Решение: P(A) = 10/1000000==0,00001·100%=0,001% . Ответ: 0,001% .
- 51. Задача №7. Найти вероятность выигрыша в мультилотерее
- 52. Решение: P(A) = 111000000 = =0,000011·100% = 0,0011%Ответ: 0,0011%.
- 53. Задача №8. Некий гражданин купил карточку лотереи
- 54. Решение: Рассмотрим событие А – угадано 3
- 55. Вывод: Азартные игры были во все времена.
- 56. Японская половица: «Расскажи, и я забуду, покажи,
- 57. Слайд 57
- 58. Ответы:
- 59. Учебник: Математика для медицинских колледжей/ М. Г.
- 60. Оцените свою работу на занятии. Было интересно
- 61. Вероятно, будет дождь; а пока жара.Вероятно, будем
- 62. Ян Амос Каменский сказал: «Считай несчастным тот
- 63. Спасибо вам за насыщенную работу. До свидания!
получение базовых знаний и формирование основных навыков по теории вероятности, необходимых для решения задач, возникающих в практической медицинской деятельности; развитие понятийной теоретико-вероятностной базы и формирование уровня алгебраической подготовки, необходимых для понимания основ теории вероятности и применения
Слайд 2получение базовых знаний и формирование основных навыков по теории вероятности, необходимых
для решения задач, возникающих в практической медицинской деятельности;
развитие понятийной теоретико-вероятностной базы и формирование уровня алгебраической подготовки, необходимых для понимания основ теории вероятности и применения знаний на практике.
развитие понятийной теоретико-вероятностной базы и формирование уровня алгебраической подготовки, необходимых для понимания основ теории вероятности и применения знаний на практике.
Цели:
Слайд 3научиться вычислять вероятности события;
вероятности событий по классическому определению;
научиться применять
теоремы сложения и умножения вероятностей для решения задач;
продемонстрировать умения самостоятельного решения вероятностных задач с помощью комбинаторики.
продемонстрировать умения самостоятельного решения вероятностных задач с помощью комбинаторики.
Задачи:
Слайд 4Людей всегда интересовало будущее. Человечество во все времена искало способ его предугадать,
или спланировать. В разное время разными способами. В современном мире есть теория, которую наука признает и пользуется для планирования и прогнозирования будущего. И эту теорию называют теорией вероятностей.
Слайд 5Вероятность - возможность исполнения, осуществимости чего - нибудь. Степень вероятности чего
- нибудь.
Определение вероятности
из толкового словаря русского языка
С.И. Ожегова и Н.Ю. Шведовой
Слайд 27Теоретический опрос
1.Дайте определения основным понятиям теории вероятности: случайное событие, достоверное событие,
невозможное событие, вероятность случайного события?
2.Сформулируйте классическое определение вероятности?
3.Сформулируйте основные теоремы теории вероятностей: теорему сложения вероятностей и теорему умножения вероятностей?
2.Сформулируйте классическое определение вероятности?
3.Сформулируйте основные теоремы теории вероятностей: теорему сложения вероятностей и теорему умножения вероятностей?
Слайд 300-1 ошибка – «5»;
2 ошибки – «4»;
3 ошибки – «3»;
4 и
более ошибок – «2».
Критерии выставления
оценок
Слайд 31Изучая понятие «вероятности», существует довольно широкий круг случайных опытов, в которых
вероятность любого события можно вычислить a priory (истина не требующая доказательств) — без проведения экспериментов — по формуле классической вероятности
Слайд 32Алгоритм решения задач на расчет вероятности по классическому определению:
Обозначить событие А.
Найти число всевозможных исходов – n.
Найти число исходов, благоприятствующих наступлению события А – m.
Найти искомую вероятность
Слайд 33Вероятность любого события не может быть меньше нуля и больше единицы,
т.е. 0≤P(A)≤1.
Невозможному событию соответствует вероятность P(A)=0, а достоверному – вероятность P(A)=1.
Невозможному событию соответствует вероятность P(A)=0, а достоверному – вероятность P(A)=1.
Слайд 34Решение задач
Задача №1. Если организаторы лотереи выпустили 1000 билетов и на
200 из них приходятся какие – либо выигрыши, а 800 билетов – без выигрыша, то вероятность того, что на один купленный билет выпадет выигрыш (А) составит …, проигрыш составит …?
(Ответ выразить в процентах).
(Ответ выразить в процентах).
Слайд 35Решение: по формуле классической вероятности нам известно общее число исходов 1000,
а благоприятных 200, используя формулу получим:
Ответ: 20% и 80%.
Ответ: 20% и 80%.
Слайд 36Задача №2. В больнице берутся десять историй болезней пациентов, которым понадобилось
переливание крови за последний месяц, и устанавливается группа крови, которая была перелита каждому из них. Среди этих пациентов у четырех человек оказалась первая группа крови, у трех – вторая, у двух – третья, у одного – четвертая группа крови. Какова вероятность того, что у выбранного наугад пациента окажется первая группа крови?
Слайд 37Решение: Обозначим через А – событие, которое заключается в том, что
у выбранного пациента окажется первая группа крови. Общее число исходов равно 10, исходов которые благоприятствуют нашему событию 4. Поэтому вероятность по формуле равна:
(первая группа крови)
Ответ: 40%.
(первая группа крови)
Ответ: 40%.
Слайд 38Задача №3. На книжной полке находятся 2 книги по микробиологии, 3
книги по химии и 1 книга по математике. Чему равна вероятность того, что случайным образом будет извлечена книга по химии или математике?
Слайд 39Решение: Обозначим через А – событие которое заключается в том, что
наугад возьмут книгу по химии, через В – событие которое заключается в том, что наугад возьмут книгу по математике. Тогда по формуле:
По теореме сложения вероятностей получим:
Ответ:
По теореме сложения вероятностей получим:
Ответ:
Слайд 40Задача №4. В коробке находится 15 медицинских инструментов, среди которых 10
пинцетов. Лаборант случайным образом извлекает из коробки 3 инструмента. Найти вероятность того, что все они окажутся пинцетами.
Слайд 41Решение: Обозначим через А событие, которое состоит в том, что все
3 извлеченных инструмента оказались пинцетами. Количество способов извлечения 3 инструментов из 15 равно числу сочетаний из 15 элементов по 3. Поэтому общее кол-во исходов равно .
Кол-во различных способов извлечения трех пинцетов из 10 равно числу сочетаний из 10 элементов по 3. Поэтому кол-во исходов, благоприятствующих событию А, равно .
Следовательно, искомая вероятность равна
Ответ: 26%.
Кол-во различных способов извлечения трех пинцетов из 10 равно числу сочетаний из 10 элементов по 3. Поэтому кол-во исходов, благоприятствующих событию А, равно .
Следовательно, искомая вероятность равна
Ответ: 26%.
Слайд 42Задача №5. Из 60 вопросов студент подготовил к экзамену 50. Какова
вероятность, что он сдаст экзамен, если билет содержит 2 вопроса?
Слайд 44«Простейший пример неоднозначной задачи: если подбросить монету, то заранее нельзя сказать,
какой стороной она ляжет вверх. Все зависит от случая. Может показаться, что в подобных задачах нет никаких закономерностей. Но что происходит при большом количестве бросков?»
Слайд 45исторические факты
Жорж Бюссон (1707-1788) бросал монету 4040 раз, и «орел» выпал
в 2048 случаях.
Слайд 47Какие из следующих событий – случайные, достоверные, невозможные:
черепаха научится говорить;
ваш день
рождения – 01 октября
ночью светит солнце;
вы выиграете, участвуя в гонках;
вы выходите на улицу на лыжах;
сегодня вы все сдадите дифф. зачет по математике;
вы не выигрываете, участвуя в беспроигрышной лотерее;
вы проиграете партию в шахматы;
после четверга будет пятница;
1 июля в Евпатории будет солнечно;
вы выходите на улицу, а навстречу вам идет слон.
на следующей неделе испортится погода;
вы нажали на звонок, а он не зазвонил;
после пятницы будет воскресенье.
ночью светит солнце;
вы выиграете, участвуя в гонках;
вы выходите на улицу на лыжах;
сегодня вы все сдадите дифф. зачет по математике;
вы не выигрываете, участвуя в беспроигрышной лотерее;
вы проиграете партию в шахматы;
после четверга будет пятница;
1 июля в Евпатории будет солнечно;
вы выходите на улицу, а навстречу вам идет слон.
на следующей неделе испортится погода;
вы нажали на звонок, а он не зазвонил;
после пятницы будет воскресенье.
Слайд 49Задача №6. Найти вероятность выигрыша в лотерее «Железнодорожная». Тираж этой лотереи
1 000 000.
В тираже разыгрываются призы: 250 000, 50 000, 10 000, 5 000, 3 000, 200, 100, 50, 40, 20 рублей. Всего – 10. Ответ выразить в процентах.
В тираже разыгрываются призы: 250 000, 50 000, 10 000, 5 000, 3 000, 200, 100, 50, 40, 20 рублей. Всего – 10. Ответ выразить в процентах.
Слайд 51Задача №7. Найти вероятность выигрыша в мультилотерее «Деньги». Тираж этой лотереи
1 000 000.
В тираже разыгрываются призы: 10, 20, 50, 100, 300, 500, 1 000,
2 000, 5 000, 50 000, 5 000 000 рублей. Всего – 11.
В тираже разыгрываются призы: 10, 20, 50, 100, 300, 500, 1 000,
2 000, 5 000, 50 000, 5 000 000 рублей. Всего – 11.
Слайд 53Задача №8. Некий гражданин купил карточку лотереи и наугад отметил в
ней 6 из имеющихся 49 номеров. Найдите вероятность того, что он правильно угадал 3 из 6 номеров, которые будут опубликованы в списке «выигравших».
Слайд 54Решение: Рассмотрим событие А – угадано 3 номера из 6 (значит,
остальные 3 не угаданы).
Итак, вероятность правильно угадать 3 номера из 6 очень не велика – около 1,8%. Ясно, что вероятность угадать 4 номера, 5 или все 6 – еще меньше.
Ответ: 0,0176 или 1,8%.
Итак, вероятность правильно угадать 3 номера из 6 очень не велика – около 1,8%. Ясно, что вероятность угадать 4 номера, 5 или все 6 – еще меньше.
Ответ: 0,0176 или 1,8%.
Слайд 55Вывод: Азартные игры были во все времена. Человек каждый раз принимает
решение: играть или нет. Манит, привлекает азартная игра быстрым обогащением, крупным выигрышем. Но, как мы видим, вероятность выигрыша очень мала.
Слайд 56Японская половица: «Расскажи, и я забуду, покажи, и я запомню, дай
попробовать, и я пойму!».
Аристотель: «Ум заключается не только в знании, но и в умении прилагать знания на деле».
Аристотель: «Ум заключается не только в знании, но и в умении прилагать знания на деле».
Слайд 59Учебник: Математика для медицинских колледжей/ М. Г. Гилярова - Изд. 4-е.
– Ростов н/Д: Феникс, 2015.- 442, с.- (среднее медицинское образование).
Стр. 294-301,
№ 110, 114, 118, 119, 120 (разобрать, решение записать в тетрадь),
№126-129, 131,135 (решить).
Стр. 294-301,
№ 110, 114, 118, 119, 120 (разобрать, решение записать в тетрадь),
№126-129, 131,135 (решить).
Задание на дом
Слайд 60Оцените свою работу на занятии.
Было интересно на занятии, но осталось
много непонятного материала.
Было трудно в понимании материала, но основную часть усвоил.
Очень легко было понять изучаемый материал.
Было трудно в понимании материала, но основную часть усвоил.
Очень легко было понять изучаемый материал.
Слайд 61Вероятно, будет дождь; а пока жара.
Вероятно, будем жить лучше, чем вчера.
Вероятно,
вечером в доме будет свет.
Может быть - хороший день, - может быть, и нет.
Этих вероятностей в жизни пруд пруди,
Только их теорию - выучи поди!
Чтобы по теории двойку не схватить,
Эти вероятности надобно учить.
Может быть - хороший день, - может быть, и нет.
Этих вероятностей в жизни пруд пруди,
Только их теорию - выучи поди!
Чтобы по теории двойку не схватить,
Эти вероятности надобно учить.
Слайд 62Ян Амос Каменский сказал: «Считай несчастным тот день или тот час,
в котором, ты не усвоил ничего, ничего не прибавил к своему образованию».