- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Первообразная
Содержание
- 1. Первообразная
- 2. Устные упражнения2x0 cos xex
- 3. Взаимно-обратные операции в математикеПрямаяОбратнаяx2Возведение в квадратsin α
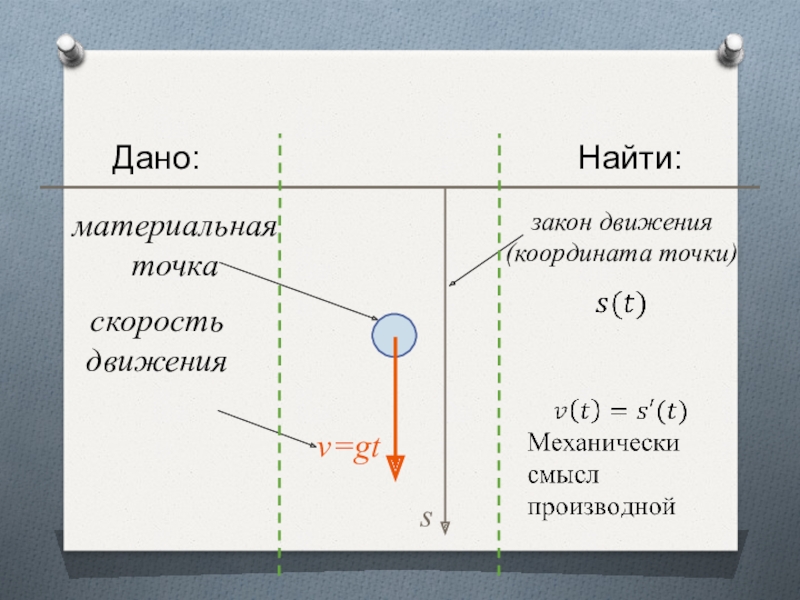
- 4. материальная точкаv=gtскоростьдвиженияsДано:Найти:закон движения(координата точки)
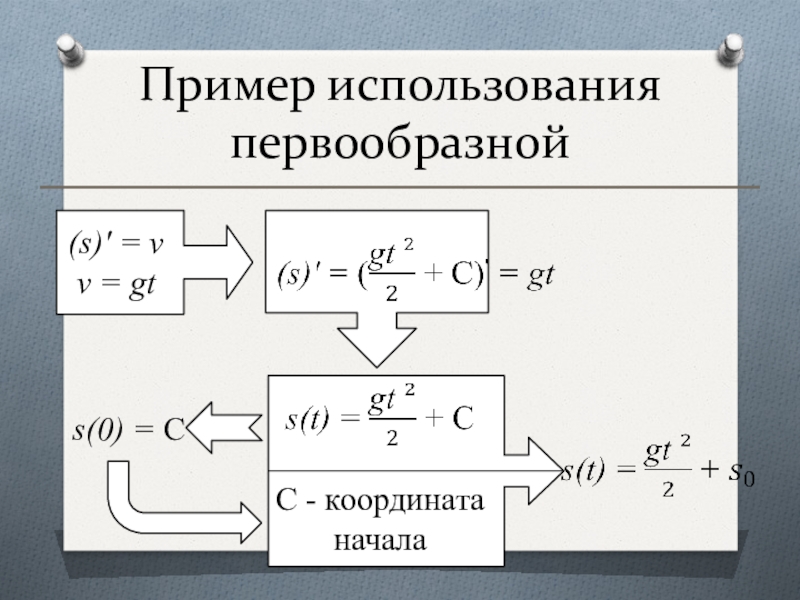
- 5. Пример использования первообразнойРешение::s' (t) = v(t)v = gt
- 6. Пример использования первообразной(s)' = vv = gt s(0) = CC - координата начала
- 7. ПервообразнаяОпределение:Функцию y = F(x) называют первообразной для
- 8. Взаимно-обратные операции в математикеПрямаяОбратнаяx2Возведение в квадратsin α
- 9. Пояснение в сравненииПроизводная"Производит" новую ф-июПервообразнаяПервичный образдифференцированиевычисление производнойинтегрированиевосстановление функции из производной
- 10. Неоднозначность первообразнойf(x) = 2xF1(x) = x2F2(x) =
- 11. Слайд 11
- 12. Слайд 12
- 13. Отработка материалаПрактические задания
- 14. Найти одну из первообразных для следующих функций1)
- 15. Док-ть, что F(x) первообразная для f(x) на
- 16. Задачи на доказательство:
- 17. Домашнее заданиеТеория:§20, определение наизустьПрактика:№ 20.1№ 20.4 (в,г)№ 20.5 (в,г)
Устные упражнения2x0 cos xex
Слайд 3Взаимно-обратные операции в математике
Прямая
Обратная
x2
Возведение в квадрат
sin α = a
Синус угла
arcsin a
= α a∈[-1;1]
Арксинус числа
Арксинус числа
Сложение
Вычитание
?
![Взаимно-обратные операции в математикеПрямаяОбратнаяx2Возведение в квадратsin α = aСинус углаarcsin a = α a∈[-1;1]Арксинус числаСложение Вычитание](/img/thumbs/e623fbbb04af338526a64b12ade0f7ff-800x.jpg "Первообразная Взаимно-обратные операции в математикеПрямаяОбратнаяx2Возведение в квадратsin α = aСинус углаarcsin a")
Слайд 7Первообразная
Определение:
Функцию y = F(x) называют первообразной для y = f(x) на
промежутке X, если при x ∈ X
F'(x) = f(x)
F'(x) = f(x)
Слайд 8Взаимно-обратные операции в математике
Прямая
Обратная
x2
Возведение в квадрат
sin α = a
Синус угла
arcsin a
= α a∈[-1;1]
Арксинус числа
Арксинус числа
F(x)
Вычисление первообразной
Сложение
Вычитание
![Взаимно-обратные операции в математикеПрямаяОбратнаяx2Возведение в квадратsin α = aСинус углаarcsin a = α a∈[-1;1]Арксинус числаF(x)Вычисление первообразной](/img/thumbs/2f88c8f11642ec98b08931e0c36b388e-800x.jpg "Первообразная Взаимно-обратные операции в математикеПрямаяОбратнаяx2Возведение в квадратsin α = aСинус углаarcsin a")
Слайд 9Пояснение в сравнении
Производная
"Производит" новую ф-ию
Первообразная
Первичный образ
дифференцирование
вычисление производной
интегрирование
восстановление функции из производной
Слайд 10Неоднозначность первообразной
f(x) = 2x
F1(x) = x2
F2(x) = x2 + 1
F3(x) =
x2 + 5
F1'(x) = 2x
F2'(x) = 2x
F3'(x) = 2x
y = f(x) имеет бесконечно много первообразных вида y = F(x)+C, где
C - произвольное число
Слайд 14Найти одну из первообразных для следующих функций
1) f(x) = 4
2) f(x)
= -1
3) f(x) = x3
4) f(x) = sin x
5) f(x) = x2 + 3cos x
3) f(x) = x3
4) f(x) = sin x
5) f(x) = x2 + 3cos x
Слайд 15Док-ть, что F(x) первообразная для f(x) на заданном промежутке
Условия
Дано: F(x)
= 3x4
Док-ть: f(x) = 12x3
при x ∈ (-∞;+∞)
Док-ть: f(x) = 12x3
при x ∈ (-∞;+∞)
Доказательство
Найдем производную F(x): F'(x) = (3x4)' = 12x3 = f(x)
F'(x) = f(x), значит
F(x) = 3x4 первообразная для f(x) = 12x3
