колледж»: Полоскова Наталья Анатольевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Открытый урок по теме Формулы приведения.
Содержание
- 1. Открытый урок по теме Формулы приведения.
- 2. Мало иметь хороший ум, главное — хорошо его применять.Рене Декарт
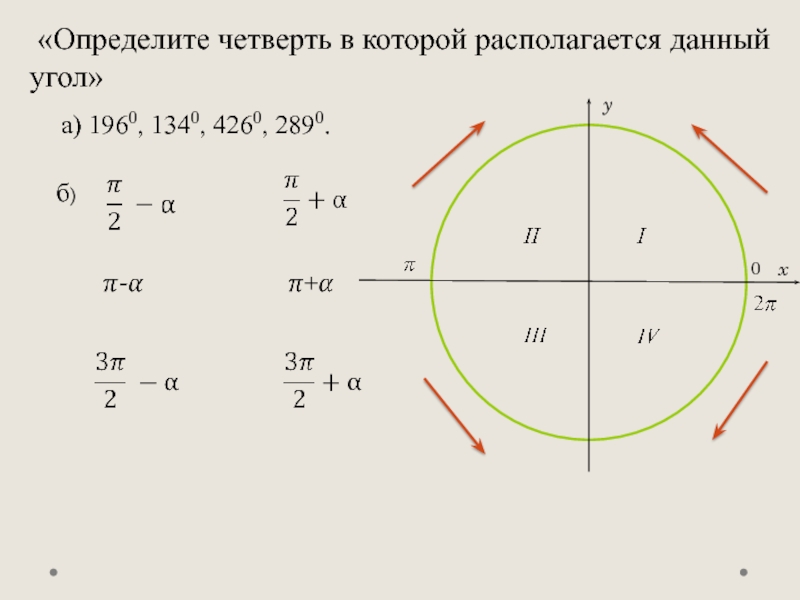
- 3. «Определите четверть в которой располагается данный угол»а) 1960, 1340, 4260, 2890. б)yx0
- 4. ФОРМУЛЫ ПРИВЕДЕНИЯ это формулы, позволяющие выражать значения
- 5. И еще один момент: формул приведения достаточно
- 6. 0xy0++
- 7. 0xy0
- 8. Правило «знаков» Знак
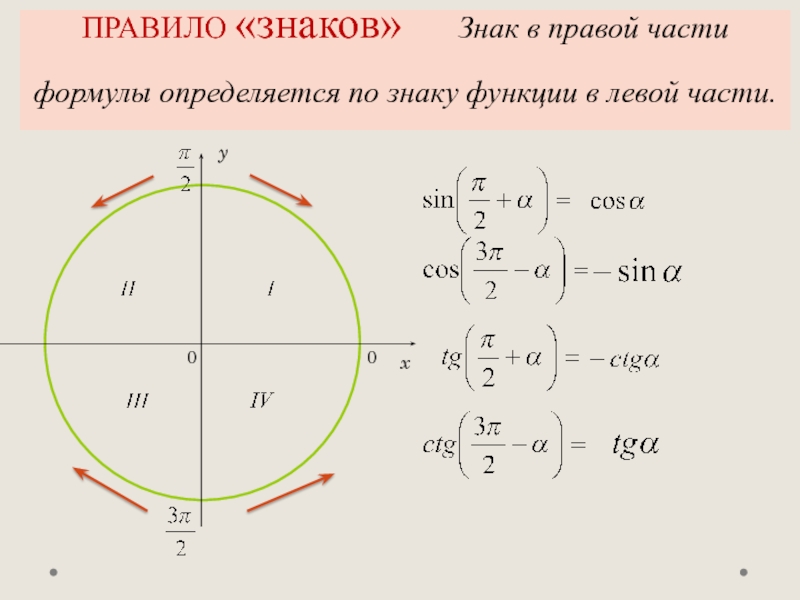
- 9. 0xy0ПРАВИЛО «знаков» Знак в правой части формулы определяется по знаку функции в левой части.
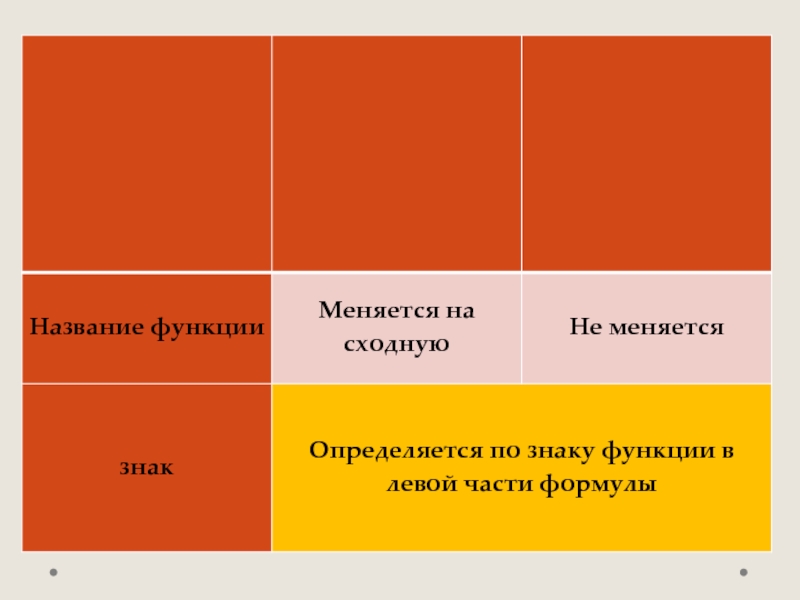
- 10. Слайд 10
- 11. Запишите формулы приведения
- 12. Одно из применений – это нахождение значений тригонометрических функций различных углов.Например:Где же применяются формулы приведения?
- 13. Задание 1. Найдите острый угол при котором выполняется равенствоЗадание 3. Используя формулы приведения вычислить:
- 14. Задание 4. Упростите выражение.
- 15. sin 131° = sin (90° + 41°)
- 16. Очевидно, перед нами снова формула приведения: 90° —
- 17. правило знаков и названий;задание в ACУ Procolledg.Домашнее задание:
- 18. Рефлексия:
- 19. Слайд 19
Мало иметь хороший ум, главное — хорошо его применять.Рене Декарт
Слайд 1ФОРМУЛЫ ПРИВЕДЕНИЯ
Открытый урок подготовила и провела преподаватель математики ГБПОУ «Южно-уральский многопрофильный
Слайд 4ФОРМУЛЫ ПРИВЕДЕНИЯ
это формулы, позволяющие выражать значения тригонометрических функций любого угла
через функции угла первой четверти, т.е. < 90°.
Формулы приведения получили свое название не от слова «привиделось», а от слова «приводить».
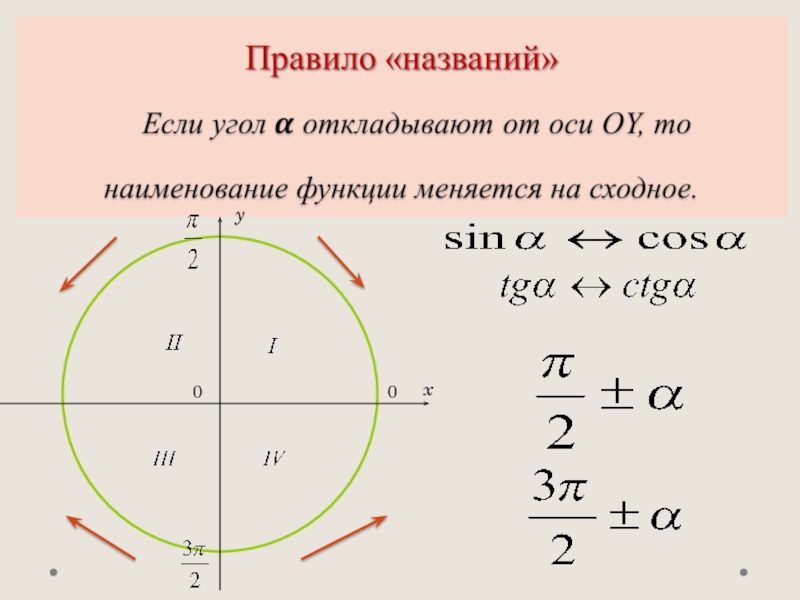
Слайд 5И еще один момент: формул приведения достаточно много по количеству, и
сразу предостережем Вас от заучивания их всех наизусть. В этом абсолютно нет необходимости – существует правило, позволяющее легко применять формулы приведения.
Слайд 8Правило «знаков» Знак в правой части формулы определяется
по знаку функции в левой части.
0
x
y
0
Слайд 90
x
y
0
ПРАВИЛО «знаков» Знак в правой части формулы определяется по
знаку функции в левой части.
Слайд 12Одно из применений – это нахождение значений тригонометрических функций различных углов.
Например:
Где
же применяются формулы приведения?
Слайд 13Задание 1. Найдите острый угол при котором выполняется равенство
Задание 3. Используя
формулы приведения вычислить:
Слайд 15sin 131° = sin (90° + 41°) = cos 41
Сначала разберемся
с числителем. cos 41° — это нетабличное значение, поэтому мы ничего не можем сделать с ним. Пока так и оставим.
Теперь смотрим на знаменатель:
Теперь смотрим на знаменатель:
Очевидно, что перед нами формула приведения, поэтому синус заменился на косинус. Кроме того, угол 41° лежит на отрезке (0°; 90°), т.е. в первой координатной четверти — именно так, как требуется для применения формул приведения. Но тогда 90° + 41° — это вторая координатная четверть. Исходная функция y = sin x там положительна, поэтому мы и поставили перед косинусом на последнем шаге знак «плюс» (другими словами не поставили ничего).
Осталось разобраться с последним элементом:
cos 240° = cos (180° + 60°) = −cos 60° = −0,5
Теперь подставляем полученные числа в исходную формулу и получаем:
Задание 5. Упростите выражение.
Слайд 16Очевидно, перед нами снова формула приведения: 90° — это вертикальная ось, следовательно,
синус поменяется на косинус. Кроме того, угол α = 117° = 90° + 27° лежит во второй координатной четверти. Исходная функция y = sin x там положительна, следовательно, перед косинусом после всех преобразований все равно остается знак «плюс». Другими словами, там ничего не добавляется — так и оставляем: cos 27°.
Задание 6. Упростите выражение.
Перед нами снова дробь:
Ну, 27° у нас лежит в первой координатной четверти, поэтому здесь ничего менять не будем. А вот sin 117° надо расписать (пока без всякого квадрата):
sin 117° = sin (90° + 27°) = cos 27°
Возвращаемся к исходному выражению, которое требуется вычислить:
