ДСВ, закон ее распределения. Понятие о законе больших чисел.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Основы теории вероятностей 1 курс
Содержание
- 1. Основы теории вероятностей 1 курс
- 2. Основные определения Всякий результат или исход
- 3. Классическое определение вероятности Невозможному событию соответствует вероятность P(A)=0, а достоверному – вероятность P(A)=1Вероятность любого события:
- 4. Теоремы сложения вероятностей Теорема сложения вероятностей
- 5. Теоремы умножения вероятностей
- 6. Слайд 6
- 7. Случайные величины
- 8. Закон распределения Для любой ДСВ
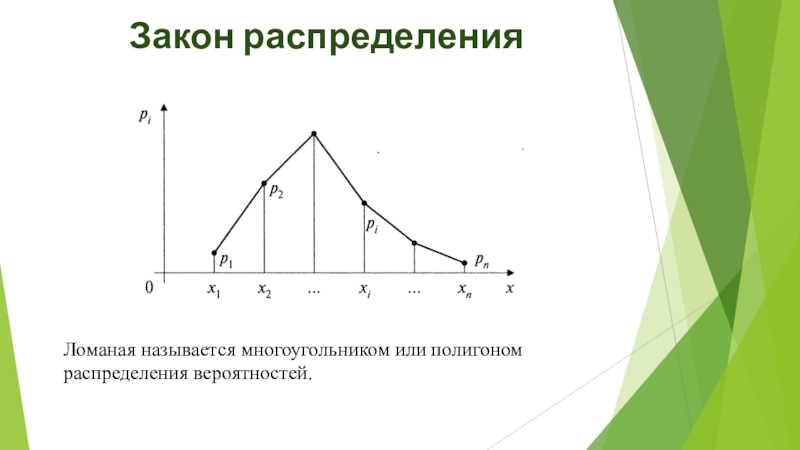
- 9. Закон распределения Ломаная называется многоугольником или полигоном распределения вероятностей.
- 10. Пример
- 11. Математическое ожидание, дисперсия, среднее квадратическое отклонение
- 12. Слайд 12
Основные определения Всякий результат или исход испытания называется событием. Если событие при заданных условиях может произойти или не произойти, то оно называется случайным. События называются несовместными, если каждый раз возможно появление только одного
Слайд 1Событие, вероятность события. Сложение и умножение вероятностей. Понятие о независимости событий.
Слайд 2Основные определения
Всякий результат или исход испытания называется событием.
Если событие при заданных условиях может произойти или не произойти, то оно называется случайным.
События называются несовместными, если каждый раз возможно появление только одного из них.
События называются совместными, если в данных условиях появление одного из этих событий не исключает появления другого при том же испытании.
События называются несовместными, если каждый раз возможно появление только одного из них.
События называются совместными, если в данных условиях появление одного из этих событий не исключает появления другого при том же испытании.
Слайд 3Классическое определение вероятности
Невозможному событию соответствует вероятность P(A)=0, а достоверному –
вероятность P(A)=1
Вероятность любого события:
Слайд 4Теоремы сложения вероятностей
Теорема сложения вероятностей несовместных событий.
Вероятность
одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P(A+B)=P(A)+P(B);
Теорема сложения вероятностей совместных событий.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
P(A+B)=P(A)+P(B) - P(AB)
P(A+B)=P(A)+P(B);
Теорема сложения вероятностей совместных событий.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
P(A+B)=P(A)+P(B) - P(AB)
Слайд 9Закон распределения
Ломаная называется многоугольником или полигоном распределения вероятностей.
