- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Обучающая программа Неравества с модулем
Содержание
- 1. Обучающая программа Неравества с модулем
- 2. СправочникОпределение 1. Неравенства вида
- 3. Справочник1. С помощью тождественных и равносильных преобразований
- 4. СправочникПример. Решите неравенство:Решение:1.2.3.4.
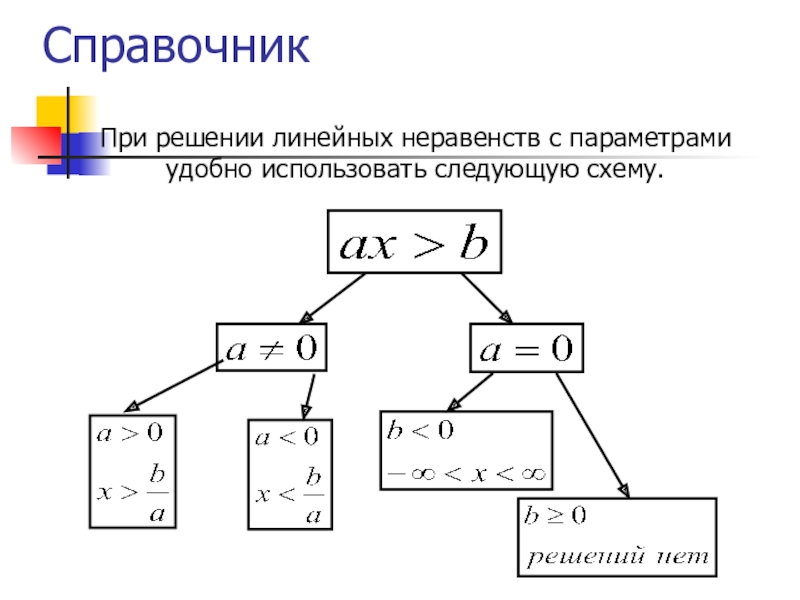
- 5. Схема решения линейных неравенств с параметромПривести неравенство
- 6. При решении линейных неравенств с параметрами удобно использовать следующую схему.Справочник
- 7. Пример. Решите неравенство:Решение:1.2.3.а)б)с)Ответ:Справочник
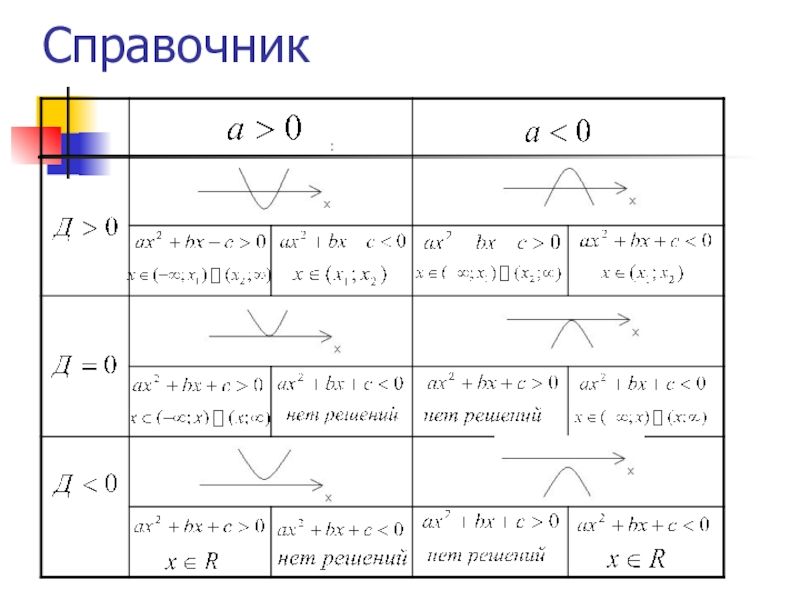
- 8. СправочникСхема решения квадратных неравенствНайти корни квадратного трехчлена
- 9. Пример. Решите неравенство:1.Решение:2.3.Справочник
- 10. Схема решения квадратных неравенств с параметромСправочникОпределить, является
- 11. Справочник
- 12. Пример. Решите неравенство:Решение:1.Так как коэффициент перед
- 13. 3.а)б)в)Справочник4.
- 14. Пример. При каких значениях
- 15. 2. Найдем корни квадратного трехчлена3. Наносим точки на числовую прямую и определяем знак.Ответ: при Справочник
- 16. Тестовое задание
- 17. Тестовое задание1. Какое линейное неравенство соответствует следующему неравенству:А)Б)В)Г)
- 18. Вы ответили правильно!!! Переходите к следующему заданию.
- 19. 2. При каких значениях неравенство
- 20. Вы ответили правильно!!! Переходите к следующему заданию.
- 21. 3. При каком условии неравенство
- 22. Вы ответили правильно!!! Переходите к следующему заданию.
- 23. 4. Решите неравенство:А)Б)В)Г)Тестовое задание
- 24. Вы ответили правильно!!! Переходите к следующему заданию.
- 25. Тестовое задание5. Решите неравенство:А)Б)В)Г)
- 26. Вы ответили правильно!!! Переходите к следующему заданию.
- 27. 6. Решите неравенство:А)Б)В)Г)Тестовое задание
- 28. Вы ответили правильно!!! Переходите к следующему заданию.
- 29. 7. Найдите все значения параметра
- 30. Вы ответили правильно!!! Молодцы!!!
- 31. Вы ответили неправильно!!! Перейдите к справочнику.
- 32. Список использованной литературыАлгебра: Учеб.для 8 кл. сред.
Слайд 2Справочник
Определение 1. Неравенства вида и
Определение 2. Неравенства вида и
, где переменная, некоторые числа, причем , называют неравенствами второй степени с одной переменной или квадратными неравенствами.
Определение 3. Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.
Слайд 3Справочник
1. С помощью тождественных и равносильных преобразований привести неравенство к виду
2. Выразить .
3. Нанести решение на координатную прямую.
4. Записать ответ
Схема решения линейных неравенств
Слайд 5Схема решения линейных неравенств с параметром
Привести неравенство к виду
2. Рассмотреть три случая:
первый - коэффициент перед больше нуля, второй – коэффициент перед меньше нуля, третий – коэффициент перед равен нулю и решить неравенство для всех случаев.
3. Записать ответ.
Справочник
Слайд 8Справочник
Схема решения квадратных неравенств
Найти корни квадратного трехчлена
2. Отметить найденные корни
; сделать набросок графика.
3. С помощью полученной геометрической модели определить, на каких промежутках оси ординаты графика положительны (отрицательны); включить эти промежутки в ответ.
Слайд 10Схема решения квадратных неравенств с параметром
Справочник
Определить, является ли неравенство квадратным.
Найти корни
Рассмотреть три случая:
первый – дискриминант больше нуля;
второй – дискриминант равен нулю;
третий – дискриминант меньше нуля.
4. Найти решение неравенства для трех случаев и записать ответ.
Слайд 12Пример. Решите неравенство:
Решение:
1.
Так как коэффициент перед равен 1
2.
Справочник
Слайд 14Пример. При каких значениях неравенство
Решение:
Чтобы неравенство выполнялось при всех ,
нужно чтобы дискриминант квадратичной функции
был меньше нуля.
1. Найдем дискриминант
Справочник
Слайд 152. Найдем корни квадратного трехчлена
3. Наносим точки на числовую прямую и
Ответ: при
Справочник
Слайд 192. При каких значениях неравенство
А)
Б)
В)
Г)
Тестовое задание
Слайд 297. Найдите все значения параметра , при которых неравенство
А)
Б)
В)
Г)
Тестовое задание
Слайд 32Список использованной литературы
Алгебра: Учеб.для 8 кл. сред. шк./ Ю. Н. Макарычев,
Алгебра: Учеб.для 9 кл. сред. шк./ МакарычевЮ. Н., МиндюкН. Г., НешковК. И., СувороваС. Б.; Под ред. ТеляковскогоС. А. - 5 - ое изд. - М.: Просвещение, 2000.
Мордкович А.Г. Алгебра 7 кл.:В двух частях. Ч.2.: Задачник для общеобразовательных учреждений – 6-е изд., испр. - М.: Мнемозина, 2003 - 160 с.; с. 87-88.
Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч. 1: Учеб. Для общеобразоват. учреждений. - 5 - е изд. - М.: Мнемозина, 2003.
Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч. 2: Учеб. Для общеобразоват. учреждений. - 5 - е изд. - М.: Мнемозина, 2003.
Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч. 1: Учеб. Для общеобразоват. учреждений. - 5 - е изд. - М.: Мнемозина, 2003.
Мордкович А.Г. Алгебра. 9 кл.: В двух частях. Ч. 2: Учеб. Для общеобразоват. учреждений. - 5 - е изд. - М.: Мнемозина, 2003.
Планирование обязательных результатов обучения математике/ Л.О. Денищева, Л.В. Кузнецова, И.А. Лурье и др.; Сост. В.В. Фирсов. - М.: Просвещение, 1989.