- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Обновление содержания, методики преподавания и качества реализации программ по математике в 5-11 классах в ОУ
Содержание
- 1. Обновление содержания, методики преподавания и качества реализации программ по математике в 5-11 классах в ОУ
- 2. Повестка дня:Обновление содержания, методики преподаванияи качества реализации
- 3. Вопросы для обсуждения1. Научить школьника
- 4. Проблемы , связанные с ГИА:Несформированность базовой логической
- 5. Для овладения содержанием учебного предмета «математика» нужны
- 6. Методические рекомендации- определить причины низких результатов по
- 7. Результаты ОГЭ и ЕГЭ 2017 по Советскому району
- 8. 184 обучающихся 9 классов из 17 школ
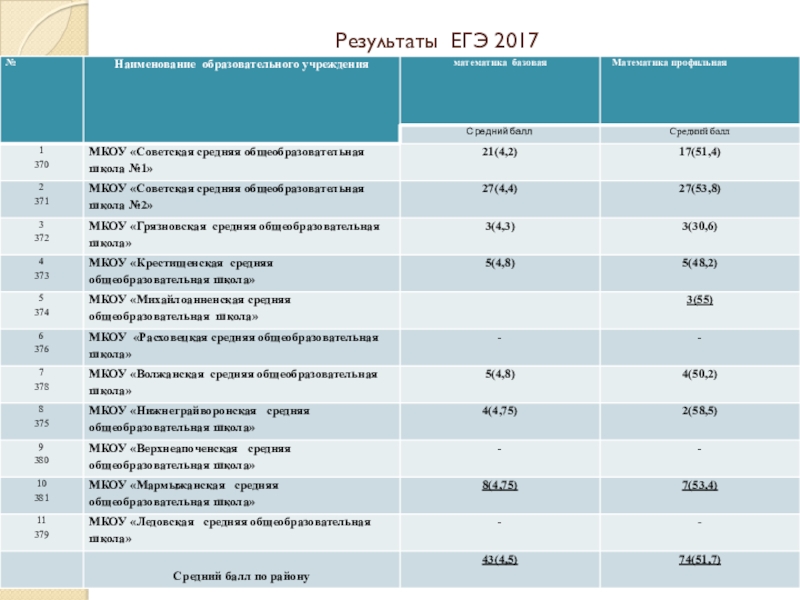
- 9. Результаты ЕГЭ 2017
- 10. Предметные результаты изучения учебного предмета «Математика» на
- 11. Уравнения и неравенства;умение оперировать на базовом уровне
- 12. Уравнения и неравенстваумение свободно оперировать понятиями: уравнение;
- 13. Векторы и координаты на плоскостиумение оперировать на
- 14. История математикиумение описывать отдельные выдающиеся результаты, полученные
- 15. Обучающиеся испытывали затруднения при решении системы уравнений
- 16. В решениях геометрических задач нет четкости изложения
- 17. Типичные ошибки, допущенные обучающимися в задании 13:решение
- 18. Типичные ошибки обучающихся, допущенные в заданиях 14:установление
- 19. Типичные ошибки обучающихся, допущенные в заданиях 15:неверное
- 20. Итоги олимпиады 2016-2017 уч.годматематика олимпиада 2016.doc
Слайд 1Обновление содержания,
методики преподавания и
качества реализации программ
по математике в
Слайд 2Повестка дня:
Обновление содержания, методики преподавания
и качества реализации программ по математике
в 5-11классах
математического образования)
ГИА: ОГЭ и ЕГЭ 2017
Итоги ярмарки инноваций
Итоги олимпиады, подготовка заданий к школьному
этапу олимпиад
Итоги НПК школьников
Конкурс педагогического мастерства
Из опыта работы
Стажировочная площадка
Слайд 3Вопросы для обсуждения
1. Научить школьника математике и
и тоже?
2. Нужно ли учить школьников
«технике выполнения заданий в
тестовой форме»?
Слайд 4Проблемы , связанные с ГИА:
Несформированность базовой логической культуры;
Недостаточные геометрические знания;
Несформированность графической
Неумение проводить анализ условия и искание путей решения,
Плохое развитие регулятивных умений:
умение находить и исправлять собственные ошибки
Неумение решать различные уравнения и неравенства, отбирать корни;
Недостаточно знаний в построении и исследовании математических моделей в соответствии с условием задачи;
Нерациональное выполнение вычислений и преобразование выражений;
Слайд 5Для овладения содержанием учебного предмета «математика» нужны осознанные знания, опосредованные в
5-6 класс: дроби (целое число, дробь, модуль числа, округление), решение уравнений (корень уравнения, решение уравнения, числовое неравенство); делимость натуральных чисел (признаки делимости, НОД и НОК );
7-9 класс: геометрические фигуры; числа (арифметический квадратный корень, иррациональные числа); уравнения и неравенства, функции (аргумент, область определения, множество значений, нули функции, промежутки знакопостоянства, промежутки возрастания и убывания, наибольшее и наименьшее значения функции); прогрессии; статистика и теория вероятностей (статистические характеристики, вероятность случайного события); векторы (сумма векторов, произведение вектора на число, координаты на плоскости).
Слайд 6Методические рекомендации
- определить причины низких результатов по выявленным разделам/темам учебной
программы, проанализировать
- планировать изучение курса с учетом его особенностей и выявленных проблем;
- организовывать повторение пройденного материала, особенно за курс основной
школы, выделяя для этого специальное время в учебном процессе;
- шире использовать в образовательном процессе индивидуальный и
дифференцированный подходы.
Слайд 8184 обучающихся 9 классов из 17 школ района были заявлены на
Слайд 10Предметные результаты изучения учебного предмета «Математика» на уровне основного общего образования
Множества, логические рассуждения;
Числа и вычисления;
Тождественные преобразования);
Уравнения и неравенства;
Функции;
Статистика и теория вероятностей
Текстовые задачи
Геометрические фигуры
Отношения
Измерения и вычисления
Геометрические построения
Геометрические преобразования
Векторы и координаты на плоскости
История математики
Методы математики
(проект ФГОС ООО, редакция 2017) Предметные результаты изучения учебного предмета «Математика (включая алгебру и геометрию)»,
Слайд 11
Уравнения и неравенства;
умение оперировать на базовом уровне понятиями: равенство, числовое равенство,
Слайд 12Уравнения и неравенства
умение свободно оперировать понятиями: уравнение; неравенство; равносильные уравнения и
Углубленный уровень
Слайд 13Векторы и координаты на плоскости
умение оперировать на базовом уровне понятиями: вектор,
Слайд 14История математики
умение описывать отдельные выдающиеся результаты, полученные в ходе развития математики
Методы математики
умение выбирать подходящий изученный метод для решения изученных типов математических задач; приводить примеры математических закономерностей в окружающей действительности и произведениях искусства; используя изученные методы, проводить доказательство, выполнять опровержение.
Слайд 15Обучающиеся испытывали затруднения при решении системы уравнений №21, причем многие выпускники
При решении текстовой задачи (№22) неправильно составляют уравнение (математическую модель реальной ситуации), допускают ошибки при решении дробно-рационального уравнения, допускают ошибки при решении полученного квадратного уравнения. При построении графика функции, содержащей модуль (№23), учащиеся демонстрируют незнание алгоритма построения графика функции вида y=|f(x)| и неумение раскрывать знак модуля.
АНАЛИЗ РЕЗУЛЬТАТОВ ВЫПОЛНЕНИЯ ОТДЕЛЬНЫХ ЗАДАНИЙ ИЛИ ГРУПП ЗАДАНИЙ ОГЭ
Слайд 16В решениях геометрических задач нет четкости изложения и точности в обосновании
Основной проблемой, как и в прежние годы, являлось неумение учащихся математически грамотно записать решение задач второй части, привести необходимые пояснения и обоснования. Такое неумение или нежелание приводит (в соответствии с критериями) к снижению балла, а иногда и к обнулению результата выполнения задания
Слайд 17Типичные ошибки, допущенные обучающимися в задании 13:
решение квадратного уравнения;
применение формул приведения;
нахождение
вычислительные ошибки.
ЕГЭ
Слайд 18Типичные ошибки обучающихся, допущенные в заданиях 14:
установление перпендикулярности, доказывалась перпендикулярность только
решение планиметрических задач, которые являются частями вычислительной части б;
вычислительные ошибки.
Слайд 19Типичные ошибки обучающихся, допущенные в заданиях 15:
неверное решение дробно-рационального неравенства;
неверный переход
вычислительные ошибки.