Презентация, доклад на тему Неопределенный интеграл

Содержание

1. Неопределенный интеграл
2. Исправьте ошибки
3. Что это за знак??? ∫
4. Неопределенный интеграл
5. Евдокс Книдский ок. 408 — ок. 355
6. Лейбниц Готфрид Вильгельм (1646-1716)Символ ∫ введен
7. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛНеопределенным интегралом от непрерывной функции f(x)
8. Таблица интегралов
9. f(x) = 2xF1(x) = x2F2(x) = x2
10. Свойства интеграла
11. Свойства интеграла
12. 1.f(x) = хn
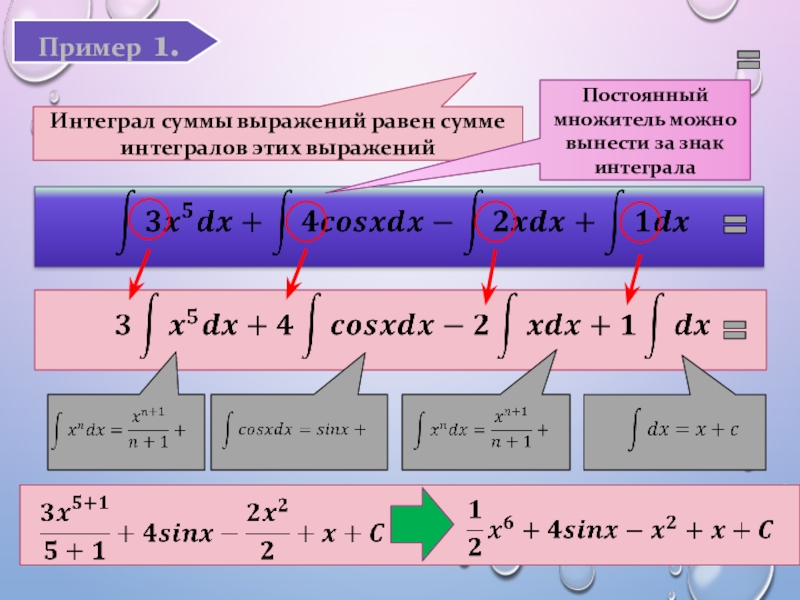
13. Пример 1.Интеграл суммы выражений равен сумме интегралов этих выражений Постоянный множитель можно вынести за знак интеграла
14. F(x) = 5 х² + CF(x) =
15. Основные методы интегрированияТабличный.2.Сведение к табличному преобразованием подынтегрального
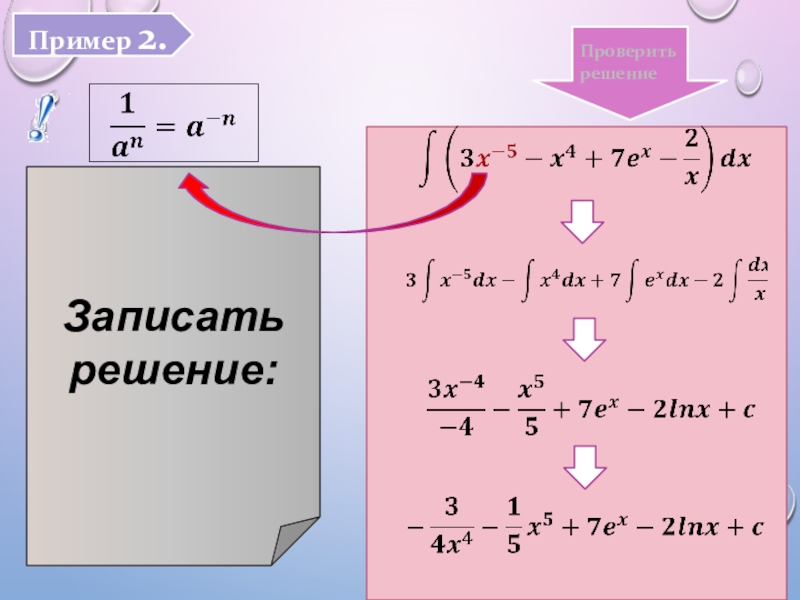
16. Пример 2.Проверитьрешение Записать решение:
17. Пример 3.Проверить решение Записать решение:
18. Верно ли что: а)
19. Домашнее задание Установить соответствие. Найти такой общий вид первообразной, которая соответствует заданной функции.

Исправьте ошибки

Слайд 1Неопределенный интеграл.
Способы вычисления

Слайд 2Исправьте ошибки

Слайд 3Что это за знак???

∫

Слайд 4Неопределенный интеграл

Слайд 5Евдокс Книдский
ок. 408 — ок. 355 год до н. э.

Интегральное исчисление появилось во времена античного периода развития математической науки и началось с метода исчерпывания, который разработан математиками Древней Греции, и представлял собой набор правил, разработанных Евдоксом Книдским. По этим правилам вычисляли площади и объёмы

Евдокс Книдский ок. 408 — ок. 355 год до н. э. Интегральное исчисление появилось во времена античного

Слайд 6Лейбниц Готфрид Вильгельм (1646-1716)
Символ ∫ введен Лейбницем (1675 г.). Этот знак

является изменением латинской буквы S (первой буквы слова summa).

Лейбниц Готфрид Вильгельм (1646-1716)Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S

Слайд 7НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Неопределенным интегралом от непрерывной функции f(x) на интервале (a; b)

называют любую ее первообразную функцию.

Где С – произвольная постоянная (const).

Слайд 8Таблица интегралов

Слайд 9f(x) = 2x
F1(x) = x2
F2(x) = x2 + 1
F3(x) = x2

+ 5

F1'(x) = 2x

F2'(x) = 2x

F3'(x) = 2x

y = f(x) имеет бесконечно много первообразных вида y = F(x)+C, где
C - произвольное число

Интегрирование обратно дифференцированию.

f(x) = 2xF1(x) = x2F2(x) = x2 + 1F3(x) = x2 + 5F1'(x) = 2xF2'(x) = 2xF3'(x)

Слайд 10Свойства интеграла

Слайд 11Свойства интеграла

Слайд 12
1.f(x) = хn

2.f(x) = C
3.f(x)=sinx

4.f(x) =

6.f(x)=

1. F(x) =Сх+С

2. F(x) =

3. F(x) =

4. F(x) = sin x+С

5. F(x) = сtg x+С

6. F(x) = - cos x+С

5.f(x) =cosx

Установить соответствие. Найти такой общий вид первообразной, которая соответствует заданной функции.

tg x+С

Слайд 13Пример 1.
Интеграл суммы выражений равен сумме интегралов этих выражений

Постоянный множитель можно

вынести за знак интеграла

Слайд 14F(x) = 5 х² + C
F(x) = х³ + C
F(x) =

-cosх +5х+ C
F(x) = 5sinx + C
F(x) = 2 х³ + C
F(x) = 3x - х²+ C

1) f(x) =10х
2) f(x) =3 х²
3) f(x) = sinх+5
4) f(x) = 5cosx
5) f(x) = 6х²
6) f(x) = 3-2х

Вычислите интегралы

F(x) = 5 х² + CF(x) = х³ + CF(x) = -cosх +5х+ CF(x) = 5sinx +

Слайд 15Основные методы интегрирования
Табличный.

2.Сведение к табличному преобразованием подынтегрального выражения в сумму или

разность.

3.Интегрирование с помощью замены переменной (подстановкой).

4.Интегрирование по частям.

Основные методы интегрированияТабличный.2.Сведение к табличному преобразованием подынтегрального выражения в сумму или разность.3.Интегрирование с помощью замены переменной (подстановкой).4.Интегрирование

Слайд 16Пример 2.

Проверить
решение

Записать решение:

Слайд 17Пример 3.
Проверить решение

Записать решение:

Слайд 18 Верно ли что:
а)

в)

б)

г)

Слайд 19 Домашнее задание Установить соответствие. Найти такой общий вид первообразной, которая

соответствует заданной функции.

Скачать презентацию

Презентация, доклад на тему Неопределенный интеграл

Содержание

Слайд 1Неопределенный интеграл.
Способы вычисления

Слайд 2Исправьте ошибки

Слайд 3Что это за знак???

∫

Слайд 4Неопределенный интеграл

Слайд 5Евдокс Книдский
ок. 408 — ок. 355 год до н. э.

Слайд 6Лейбниц Готфрид Вильгельм (1646-1716)
Символ ∫ введен Лейбницем (1675 г.). Этот знак

Слайд 7НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Неопределенным интегралом от непрерывной функции f(x) на интервале (a; b)

Слайд 8Таблица интегралов

Слайд 9f(x) = 2x
F1(x) = x2
F2(x) = x2 + 1
F3(x) = x2

Слайд 10Свойства интеграла

Слайд 11Свойства интеграла

Слайд 12
1.f(x) = хn

Слайд 13Пример 1.
Интеграл суммы выражений равен сумме интегралов этих выражений

Постоянный множитель можно

Слайд 14F(x) = 5 х² + C
F(x) = х³ + C
F(x) =

Слайд 15Основные методы интегрирования
Табличный.

2.Сведение к табличному преобразованием подынтегрального выражения в сумму или

Слайд 16Пример 2.

Проверить
решение

Записать решение:

Слайд 17Пример 3.
Проверить решение

Записать решение:

Слайд 18 Верно ли что:
а)

Слайд 19 Домашнее задание Установить соответствие. Найти такой общий вид первообразной, которая

Что такое shareslide.ru?

Обратная связь

Презентация, доклад на тему Неопределенный интеграл

Содержание

Слайд 1Неопределенный интеграл.Способы вычисления

Слайд 2Исправьте ошибки

Слайд 3Что это за знак??? ∫

Слайд 4Неопределенный интеграл

Слайд 5Евдокс Книдский ок. 408 — ок. 355 год до н. э.

Слайд 6Лейбниц Готфрид Вильгельм (1646-1716)Символ ∫ введен Лейбницем (1675 г.). Этот знак

Слайд 7НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛНеопределенным интегралом от непрерывной функции f(x) на интервале (a; b)

Слайд 8Таблица интегралов

Слайд 9f(x) = 2xF1(x) = x2F2(x) = x2 + 1F3(x) = x2

Слайд 10Свойства интеграла

Слайд 11Свойства интеграла

Слайд 121.f(x) = хn

Слайд 13Пример 1.Интеграл суммы выражений равен сумме интегралов этих выражений Постоянный множитель можно

Слайд 14F(x) = 5 х² + CF(x) = х³ + CF(x) =

Слайд 15Основные методы интегрированияТабличный.2.Сведение к табличному преобразованием подынтегрального выражения в сумму или

Слайд 16Пример 2.Проверитьрешение Записать решение:

Слайд 17Пример 3.Проверить решение Записать решение:

Слайд 18 Верно ли что: а)

Слайд 19 Домашнее задание Установить соответствие. Найти такой общий вид первообразной, которая

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 1Неопределенный интеграл.
Способы вычисления

Слайд 3Что это за знак???

∫

Слайд 5Евдокс Книдский
ок. 408 — ок. 355 год до н. э.

Слайд 6Лейбниц Готфрид Вильгельм (1646-1716)
Символ ∫ введен Лейбницем (1675 г.). Этот знак

Слайд 7НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Неопределенным интегралом от непрерывной функции f(x) на интервале (a; b)

Слайд 9f(x) = 2x
F1(x) = x2
F2(x) = x2 + 1
F3(x) = x2

Слайд 12
1.f(x) = хn

Слайд 13Пример 1.
Интеграл суммы выражений равен сумме интегралов этих выражений

Постоянный множитель можно

Слайд 14F(x) = 5 х² + C
F(x) = х³ + C
F(x) =

Слайд 15Основные методы интегрирования
Табличный.

2.Сведение к табличному преобразованием подынтегрального выражения в сумму или

Слайд 16Пример 2.

Проверить
решение

Записать решение:

Слайд 17Пример 3.
Проверить решение

Записать решение:

Слайд 18 Верно ли что:
а)