- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Научная работа на тему Лист Мебиуса 5 класс
Содержание
- 1. Научная работа на тему Лист Мебиуса 5 класс
- 2. Цель работыЦель исследовательской работы: Изучить лист Мебиуса.Мною
- 3. Способы реализации целиДля реализации цели и задач
- 4. История создания Таинственный и знаменитый лист
- 5. История созданияИдея пришла ему в голову, когда служанка неправильно сшила ленту.
- 6. Изготовление листа Мебиуса Чтобы изготовить лист Мёбиуса,
- 7. Свойства Листа Мебиуса
- 8. Опыт №1 Раскрасим обычное кольцо разными красками. Вывод: Кольцо окрасится с двух сторон
- 9. Опыт №2 Раскрасим ленту Мёбиуса Вывод:
- 10. Опыт №3 На обычное кольцо поместим два
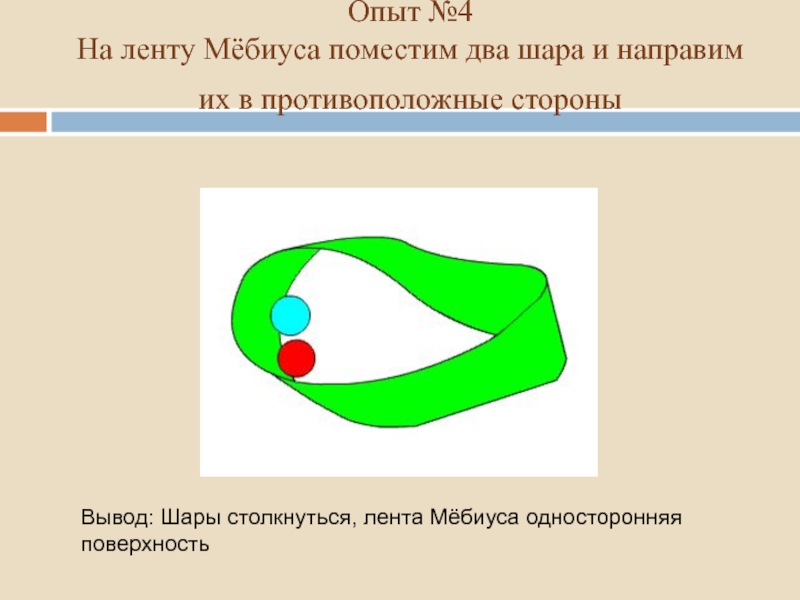
- 11. Опыт №4 На ленту Мёбиуса поместим два
- 12. Опыт №5 Закрасим узенькую полоску краяВывод: Контур Листа Мебиуса тоже бесконечен.
- 13. Топология Лист Мёбиуса - топологический объект,
- 14. Топология Топология известна и под именем
- 15. Топология На листе Мёбиуса любая точка
- 16. Сюрпризы ленты Мебиуса
- 17. Лист МёбиусаРазделим ленту пополам, разрезая её посередине
- 18. Лист МёбиусаЕсли теперь эту ленту разрезать посередине, то получаются две ленты намотанные друг на друга.
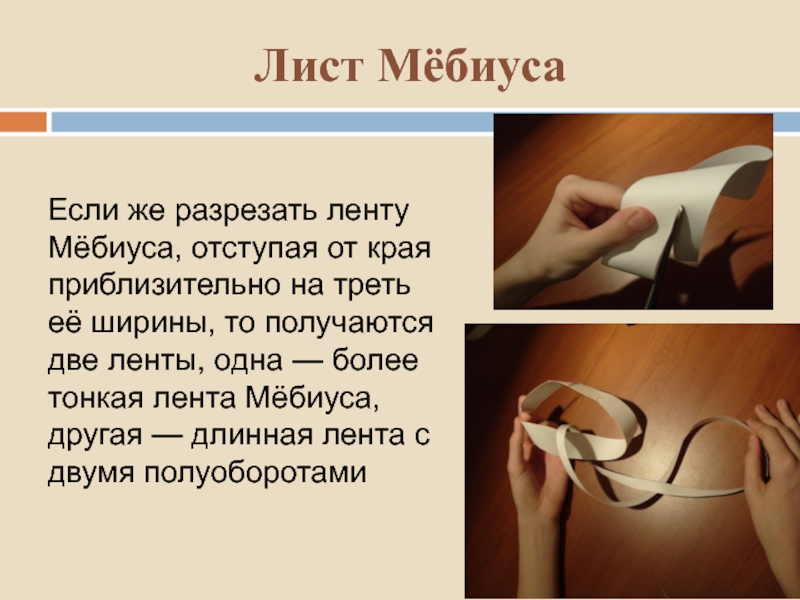
- 19. Лист Мёбиуса Если же разрезать ленту Мёбиуса,
- 20. Бутылка Клейна – односторонняя поверхностьЕсли Лист Мебиуса
- 21. Применение Лента Мёбиуса понравилась не только
- 22. Применение в техникеВинты, мешалкаЛенты для шлифовкиТрансформаторФильтр
- 23. Ленты Мёбиуса встречается в названиях художественных произведений, общественных заведений, логотипах.
- 24. Главная ценность листа МебиусаКонечно же, главная ценность
- 25. Лента Мёбиуса вдохновила многих художников на создание известных скульптур, картин.
- 26. Лента Мёбиуса вдохновила многих художников на создание известных скульптур, картин.
- 27. Лента Мёбиуса вдохновила многих художников на создание известных скульптур, картин.
- 28. Лента Мёбиуса вдохновила многих художников на создание известных скульптур, картин.
- 29. Лента Мёбиуса вдохновила многих художников на создание известных скульптур, картин.
- 30. Лента Мёбиуса вдохновила многих художников на создание известных скульптур, картин.
- 31. Лента Мёбиуса вдохновила многих художников на создание известных скульптур, картин.
- 32. Лента Мёбиуса вдохновила многих художников на создание известных скульптур, картин.
- 33. Лента Мёбиуса вдохновила многих художников на создание известных скульптур, картин.
- 34. Историческая справкаВ 1967 году, когда в Бразилии
- 35. Историческая справкаИ монумент высотой более чем в
- 36. Лист МёбиусаЛист Мёбиуса – желтая страница, Односторонний
- 37. Выводы Лист Мебиуса имеет один край. Лист
- 38. Выводы Лист Мёбиуса находит многочисленные применения в
Цель работыЦель исследовательской работы: Изучить лист Мебиуса.Мною были поставлены задачи:Собрать всевозможную информацию о листе МебиусаИзготовить лист МебиусаИсследовать опытным путем свойства листа Мебиуса.Объект исследования: лист Мебиуса.
Слайд 2Цель работы
Цель исследовательской работы:
Изучить лист Мебиуса.
Мною были поставлены задачи:
Собрать всевозможную
информацию о листе Мебиуса
Изготовить лист Мебиуса
Исследовать опытным путем свойства листа Мебиуса.
Объект исследования: лист Мебиуса.
Изготовить лист Мебиуса
Исследовать опытным путем свойства листа Мебиуса.
Объект исследования: лист Мебиуса.
Слайд 3Способы реализации цели
Для реализации цели и задач исследования я использовал следующие
методы:
анализ литературы по исследуемой теме;
практическое моделирование листа Мебиуса;
опыты.
анализ литературы по исследуемой теме;
практическое моделирование листа Мебиуса;
опыты.
Слайд 4История создания
Таинственный и знаменитый лист Мёбиуса придумал в 1858
году немецкий геометр Август Фердинанд Мёбиус (1790 - 1868), ученик «короля математиков» Гаусса.
Слайд 6Изготовление листа Мебиуса
Чтобы изготовить лист Мёбиуса,
возьмём прямоугольную полоску
и перекрутим
её на 180 градусов и
склеим противоположные стороны
склеим противоположные стороны
Слайд 9Опыт №2
Раскрасим ленту Мёбиуса
Вывод: Лента Мёбиуса окрасится в один цвет,
лента Мёбиуса –односторонняя поверхность
Слайд 10Опыт №3
На обычное кольцо поместим два шара
Вывод: Шары будут кататься
каждый по своей стороне
Слайд 11Опыт №4 На ленту Мёбиуса поместим два шара и направим их в
противоположные стороны
Вывод: Шары столкнуться, лента Мёбиуса односторонняя поверхность
Слайд 13Топология
Лист Мёбиуса - топологический объект, односторонняя поверхность с краем.
Сама топология началась именно с листа Мёбиуса. Слово «топология» придумал Иоганн Бенедикт Листинг.
Слайд 14Топология
Топология известна и под именем «резиновая геометрия».
Здесь
любую фигуру можно сгибать, скручивать, сжимать и растягивать – делать с ней всё что угодно, только не разрывать и не склеивать. И при этом , все её свойства остаются неизменными.
Слайд 15Топология
На листе Мёбиуса любая точка может быть соединена с
любой другой точкой.
На гравюре Эшера муравей будет ползти по ленте бесконечно.
На гравюре Эшера муравей будет ползти по ленте бесконечно.
Слайд 17Лист Мёбиуса
Разделим ленту пополам, разрезая её посередине по линии, параллельной краю.
Вместо двух лент получится одна длинная лента с двумя полуоборотами.
Слайд 18Лист Мёбиуса
Если теперь эту ленту разрезать посередине, то получаются две ленты
намотанные друг на друга.
Слайд 19Лист Мёбиуса
Если же разрезать ленту Мёбиуса, отступая от края приблизительно
на треть её ширины, то получаются две ленты, одна — более тонкая лента Мёбиуса, другая — длинная лента с двумя полуоборотами
Слайд 20Бутылка Клейна – односторонняя поверхность
Если Лист Мебиуса – «условно двумерный объект»
(он получен из плоской полоски), то его подружка - Бутылка Клейна полноправно занимает 3 измерения.
Слайд 21Применение
Лента Мёбиуса понравилась не только математикам, но и фокусникам.
Более 100 лет лента Мёбиуса используется для показа различных фокусов и развлечений.
Слайд 23Ленты Мёбиуса встречается в названиях художественных произведений, общественных заведений, логотипах.
Слайд 24Главная ценность листа Мебиуса
Конечно же, главная ценность листа Мёбиуса состоит в
том, что он дал толчок новым обширным математическим исследованиям.
Слайд 34Историческая справка
В 1967 году, когда в Бразилии состоялся международный математический конгресс,
его устроители выпустили памятную марку достоинством в пять сентаво. На ней была изображена лента Мёбиуса.
У входа в Музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента, закрученная на полвитка.
У входа в Музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента, закрученная на полвитка.
Слайд 35Историческая справка
И монумент высотой более чем в два метра, и крохотная
марка – своеобразные памятники немецкому математику и астроному Августу Фердинанду Мёбиусу.
Слайд 36Лист Мёбиуса
Лист Мёбиуса – желтая страница,
Односторонний сказочный маршрут,
Летит метелью,
песенкой, синицей,
Бульварной лентой, склеенный лоскут.
Эх, Мёбиус, спасибо за науку!
Поверхность одинокой стороны
Подобна закольцованному звуку,
Вибрацией неоновой струны.
Бульварной лентой, склеенный лоскут.
Эх, Мёбиус, спасибо за науку!
Поверхность одинокой стороны
Подобна закольцованному звуку,
Вибрацией неоновой струны.
Слайд 37Выводы
Лист Мебиуса имеет один край.
Лист Мебиуса имеет одну сторону.
Лист Мёбиуса - топологический объект. Как и любая топологическая фигура лента Мёбиуса не меняет своих свойств, пока ее не разрезают, не разрывают или не склеивают его отдельные куски.
Один край и одна сторона листа Мебиуса не связаны с его положением в пространстве, не связаны с понятиями расстояния.
Один край и одна сторона листа Мебиуса не связаны с его положением в пространстве, не связаны с понятиями расстояния.
Слайд 38Выводы
Лист Мёбиуса находит многочисленные применения в науке, технике и изучении
свойств Вселенной.
Лента Мебиуса вдохновляет многих художников на создание скульптур и картин.
Чудесные свойства ленты порождают множество научных трудов, изобретений (весьма полезных и совершенно нереальных), а также множество фантастических рассказов.
Лента Мебиуса вдохновляет многих художников на создание скульптур и картин.
Чудесные свойства ленты порождают множество научных трудов, изобретений (весьма полезных и совершенно нереальных), а также множество фантастических рассказов.