- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Наглядное пособие по теме Множества (для студентов)
Содержание
- 1. Наглядное пособие по теме Множества (для студентов)
- 2. ОбъединениеОбъединением (суммой) двух множеств А и В
- 3. Примеры:1) А-множество карандашей теплого оттенка в упаковке,
- 4. Свойства объединения:1. Коммутативность (переместительность):
- 5. Пересечение Пересечением множеств А и В называется
- 6. Примеры:1) А={1,3,5,7,9}, B={2,3,4,5,7,8}. Тогда А∩В={3,5,7}2) А-множество букв
- 7. Свойства пересечения1. Коммутативность А∩В=В∩А2. Ассоциативность:(А∩В)∩С=А∩(В∩С)3. Идемпотентность:А∩А=А4. Если
- 8. Дополнение Дополнением к множеству А называется множество
- 9. Примеры:1)Дополнением множества всех треугольников во множестве многоугольников
- 10. Разность Разностью двух множеств А и В
- 11. Примеры:1) А-множество учеников 5-го класса, В-множество мальчиков
- 12. Свойства дополнения и вычитания1. Аʹ∩А=Ø2. АʹυА=U3. Законы
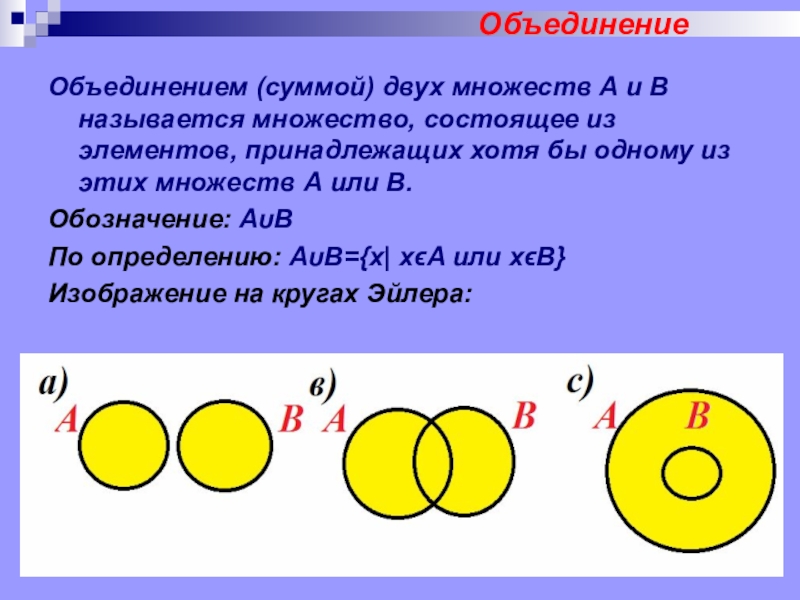
ОбъединениеОбъединением (суммой) двух множеств А и В называется множество, состоящее из элементов, принадлежащих хотя бы одному из этих множеств А или В.Обозначение: АυВПо определению: АυВ={x| xϵA или хϵВ} Изображение на кругах Эйлера:
Слайд 2Объединение
Объединением (суммой) двух множеств А и В называется множество, состоящее из
элементов, принадлежащих хотя бы одному из этих множеств А или В.
Обозначение: АυВ
По определению: АυВ={x| xϵA или хϵВ}
Изображение на кругах Эйлера:
Обозначение: АυВ
По определению: АυВ={x| xϵA или хϵВ}
Изображение на кругах Эйлера:
Слайд 3
Примеры:
1) А-множество карандашей теплого оттенка в упаковке, В-множество карандашей холодного оттенка
в упаковке, тогда АυВ=С – множество карандашей в упаковке.
2) Пусть А={1,4,6,7}, B={2,3,5,8}. Тогда АυВ={1,2,3,4,5,6,7,8}.
2) Пусть А={1,4,6,7}, B={2,3,5,8}. Тогда АυВ={1,2,3,4,5,6,7,8}.
Слайд 4Свойства объединения:
1. Коммутативность (переместительность):
АυВ=ВυА
2. Ассоциативность (сочетательность):
(АυВ)υС=Аυ(ВυС)
3. Идемпотентность (рефлексивность):
АυА=А
4. Если А подмножество В, то АυВ=В
5. Поглощение:
АυØ=А
АυU=U
3. Идемпотентность (рефлексивность):
АυА=А
4. Если А подмножество В, то АυВ=В
5. Поглощение:
АυØ=А
АυU=U
Слайд 5Пересечение
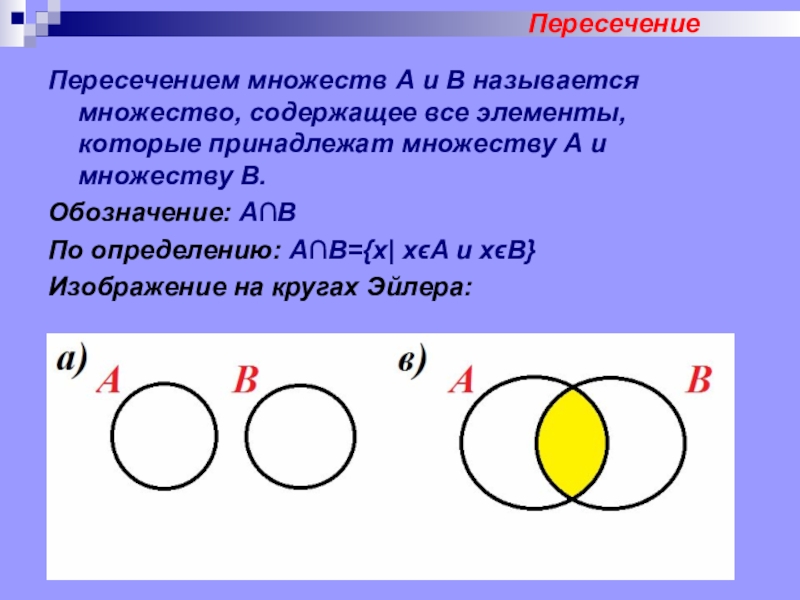
Пересечением множеств А и В называется множество, содержащее все элементы,
которые принадлежат множеству А и множеству В.
Обозначение: А∩В
По определению: А∩В={x| xϵA и xϵB}
Изображение на кругах Эйлера:
Обозначение: А∩В
По определению: А∩В={x| xϵA и xϵB}
Изображение на кругах Эйлера:
Слайд 6Примеры:
1) А={1,3,5,7,9}, B={2,3,4,5,7,8}. Тогда А∩В={3,5,7}
2) А-множество букв слова «тир», В-множество букв
слова «рота». А∩В=С – множество букв «т» и «р».
Слайд 7Свойства пересечения
1. Коммутативность
А∩В=В∩А
2. Ассоциативность:
(А∩В)∩С=А∩(В∩С)
3. Идемпотентность:
А∩А=А
4. Если А подмножество В, то
А∩В=А
5. Поглощение:
А∩Ø=Ø
А∩U=А
Законы дистрибутивности (распределительные законы)
(АυВ)∩С=(А∩С)υ(В∩С)
(А∩В)υС=(АυС)∩(ВυС)
5. Поглощение:
А∩Ø=Ø
А∩U=А
Законы дистрибутивности (распределительные законы)
(АυВ)∩С=(А∩С)υ(В∩С)
(А∩В)υС=(АυС)∩(ВυС)
Слайд 8Дополнение
Дополнением к множеству А называется множество тех элементов, которые не
входят в А и обозначаются Аʹ
Дополнение Аʹ множества А берется относительно универсального множества.
Если В подмножество А, то дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В. ВʹА={х| xϵA и хɇВ}
Изображение на кругах Эйлера:
Дополнение Аʹ множества А берется относительно универсального множества.
Если В подмножество А, то дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В. ВʹА={х| xϵA и хɇВ}
Изображение на кругах Эйлера:
Слайд 9Примеры:
1)Дополнением множества всех треугольников во множестве многоугольников является множество многоугольников с
иным количеством углов.
2)Дополнением всех положительных чисел во множестве действительных чисел является множество отрицательных чисел.
2)Дополнением всех положительных чисел во множестве действительных чисел является множество отрицательных чисел.
Слайд 10Разность
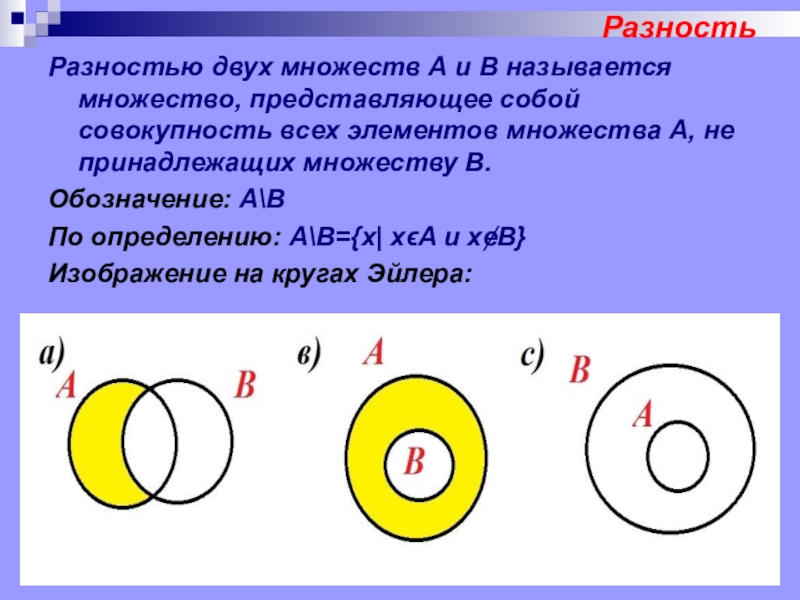
Разностью двух множеств А и В называется множество, представляющее собой
совокупность всех элементов множества А, не принадлежащих множеству В.
Обозначение: А\В
По определению: А\В={x| xϵA и xɇB}
Изображение на кругах Эйлера:
Обозначение: А\В
По определению: А\В={x| xϵA и xɇB}
Изображение на кругах Эйлера:
Слайд 11Примеры:
1) А-множество учеников 5-го класса, В-множество мальчиков 5-го класса. А\В=С –
множество девочек 5-го класса.
2) А={2,3,5,7,9}, B={1,2,4,5,6,7,8}. Тогда А\В={3,9}
2) А={2,3,5,7,9}, B={1,2,4,5,6,7,8}. Тогда А\В={3,9}
Слайд 12Свойства дополнения и вычитания
1. Аʹ∩А=Ø
2. АʹυА=U
3. Законы де Моргана:
(А∩В)ʹ=АʹυВʹ
(АυВ)ʹ=Аʹ∩Вʹ
4. Øʹ=U
5. Uʹ=Ø
6.
(A\B)\C=A\(BυC)=(A\B)∩(A\C)
7. (А\В)υВ=АυВ
8. А\(В∩С)=(А\В)υ(А\С)
9. Закон двойного отрицания (инволюция):
(Аʹ)ʹ=А
10. А\В=А∩Вʹ
7. (А\В)υВ=АυВ
8. А\(В∩С)=(А\В)υ(А\С)
9. Закон двойного отрицания (инволюция):
(Аʹ)ʹ=А
10. А\В=А∩Вʹ