- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Методика работы с алгоритмами.
Содержание
- 1. Методика работы с алгоритмами.
- 2. Происхождение слова «алгоритм» связано с именем великого математика
- 3. Абу́ Абдулла́х (или Абу Джафар) Муха́ммад ибн Муса́ аль-Хорезми́ (араб. 783,Хива Хива ,ХорезмХива ,Хорезм — ок. 850Хива ,Хорезм — ок. 850, Багдад)
- 4. Общие сведения «Алгоритм» и «правило» - близкие
- 5. Правило – разновидность предписания, в котором не
- 6. Этапы работы с алгоритмом Введение алгоритмаЦель этапа:
- 7. Свойства алгоритма Массовости – подразумевает возможность решать
- 8. Способы введения алгоритма сообщение готового алгоритма;подведение к
- 9. Обучение алгоритмам должно строиться с учетом принципов: создание
- 10. Способы их представления алгоритма • Словесно-формульное описание • Блок-схема (схема графических символов) • Программа действий
- 11. Общая схема организации учебного процесса в соответствии
- 12. Сложение алгебраических дробей. 1. Разложить знаменатель каждой дроби
- 13. РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙв=0ах2+с=0с=0ах2+вх=0в=0,с=0ах2=0 1.Перенос с
- 14. Уравнение не имеет действительных корней D0D=0РЕШЕНИЕ ПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ
- 15. aНеравенство sint > a Алгоритм решения0xy1. Отметить
- 16. На Оу отмечаем значение
- 17. 3π-t1Неравенство sint ≤ a Алгоритм0xy1. Отметить на
- 18. На Оу отмечаем значение
- 19. t1Неравенство cost > a Алгоритм решения0xy1. Отметить
- 20. На Ох отмечаем значение
- 21. Неравенство cost ≤ a Алгоритм0xy1. Отметить
- 22. На Оx отмечаем значение
- 23. Организация изучения правила умножения десятичных дробейМотивационная задача:
- 24. Решение задачи:S = v∙t4,6∙3 = 4,6 +
- 25. Нельзя ли найти более простой способ умножения?Сравним:
- 26. Оперирование в режиме пошагового контроля0,3 ∙ 1,08
- 27. В учебном процессе необходимо чаще практиковать перевод
Слайд 2Происхождение слова «алгоритм» связано с именем великого математика Мухаммеда аль-Хорезми. Основной период
Слайд 3Абу́ Абдулла́х
(или Абу Джафар) Муха́ммад ибн Муса́ аль-Хорезми́
(араб. 783,
Хива Хива ,ХорезмХива ,Хорезм — ок. 850Хива ,Хорезм — ок. 850, Багдад)
Слайд 4Общие сведения
«Алгоритм» и «правило» - близкие по значению понятия, являющиеся
Алгоритм – общепринятое и однозначное предписание, определяющее процесс преобразования исходных данных в искомый результат.
Алгоритм указывает какие операции и в какой последовательности необходимо выполнять с данными, чтобы решить любую задачу определенного типа.
Слайд 5Правило – разновидность предписания, в котором не выполняется свойство детерминированности, что
Любой алгоритм – правило,
но не любое правило – алгоритм .
Слайд 6Этапы работы с алгоритмом
Введение алгоритма
Цель этапа: актуализация знаний, необходимых для
Усвоение алгоритма
Цель этапа: отработка отдельных операций, входящих в алгоритм, разворачивание правила в алгоритм и усвоение последовательности операций.
Применение алгоритма
Цель этапа: отработка умения применять алгоритм в знакомых и незнакомых ситуациях.
Слайд 7Свойства алгоритма
Массовости – подразумевает возможность решать все задачи определенного типа.
Элементарности
Детерминированности – подразумевает однозначное выполнение каждого шага от первого до последнего.
Результативности – подразумевает, что конечное число шагов должно обязательно привести к результату.
Слайд 8Способы введения алгоритма
сообщение готового алгоритма;
подведение к самостоятельному открытию алгоритма.
Преобладающие формы работы
этап введения – устная работа;
этап усвоения – коллективная письменная работа;
этап применения – самостоятельная работа.
Слайд 9Обучение алгоритмам должно строиться с учетом принципов:
создание у учащихся полной ориентировочной основы
использование приемов, раскрывающих происхождение алгоритмов;
алгоритмизация всего процесса обучения математике в школе;
развитие логической культуры учащихся;
обеспечение взаимосвязи алгоритмов;
формирование основных компонентов алгоритмической культуры учащихся.
Слайд 10Способы их представления алгоритма
• Словесно-формульное описание
• Блок-схема (схема графических символов)
•
Слайд 11Общая схема организации учебного процесса в соответствии с теорией поэтапного формирования
формирование мотивации соответствующей деятельности;
представление основного содержания подлежащего усвоению материала в краткой схематической форме;
организация работы учащихся, позволяющей контролировать и ее ход, и ее результат;
организация постепенного перехода от пошагового контроля к самоконтролю.
Слайд 12Сложение алгебраических дробей.
1. Разложить знаменатель каждой дроби на множители:
2. Найти общий
3. Найти дополнительные множители к каждой дроби:
4. Умножить дополнительный множитель на числитель каждой дроби и между полученными произведениями поставить знак «+» или «–», указанные между дробями
5. Упростить полученную дробь:
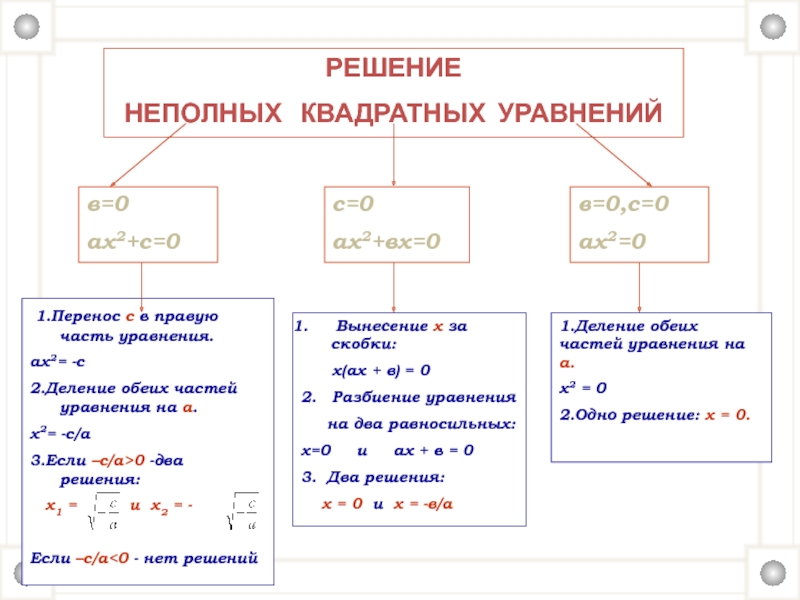
Слайд 13РЕШЕНИЕ
НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ
в=0
ах2+с=0
с=0
ах2+вх=0
в=0,с=0
ах2=0
1.Перенос с в правую часть уравнения.
ах2=
2.Деление обеих частей уравнения на а.
х2= -с/а
3.Если –с/а>0 -два решения:
х1 = и х2 = -
Если –с/а<0 - нет решений
Вынесение х за скобки:
х(ах + в) = 0
2. Разбиение уравнения
на два равносильных:
х=0 и ах + в = 0
3. Два решения:
х = 0 и х = -в/а
1.Деление обеих частей уравнения на а.
х2 = 0
2.Одно решение: х = 0.
Слайд 15a
Неравенство sint > a
Алгоритм решения
0
x
y
1. Отметить на оси ординат интервал y
2.Выделить дугу окружности, соответствующую интервалу.
3. Выбрать положительный обход дуги ( против часовой стрелки)
4.Записать числовые значения граничных точек, при этом начало дуги- меньшее значение
5. Записать общее решение неравенства.
t1
π-t1
-1
1
Слайд 16
На Оу отмечаем значение
и соответствующие точки на
окружности.
Выделяем верхнюю часть
окружности (обход совершаем
против часовой стрелки).
Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение.
4. Ответ:
Слайд 173π-t1
Неравенство sint ≤ a
Алгоритм
0
x
y
1. Отметить на оси ординат интервал y≤a.
2.
3. Выбрать положительный обход дуги ( против часовой стрелки)
4.Записать числовые значения граничных точек, при этом начало дуги- меньшее значение
4. Записать общее решение неравенства.
a
t1
-1
1
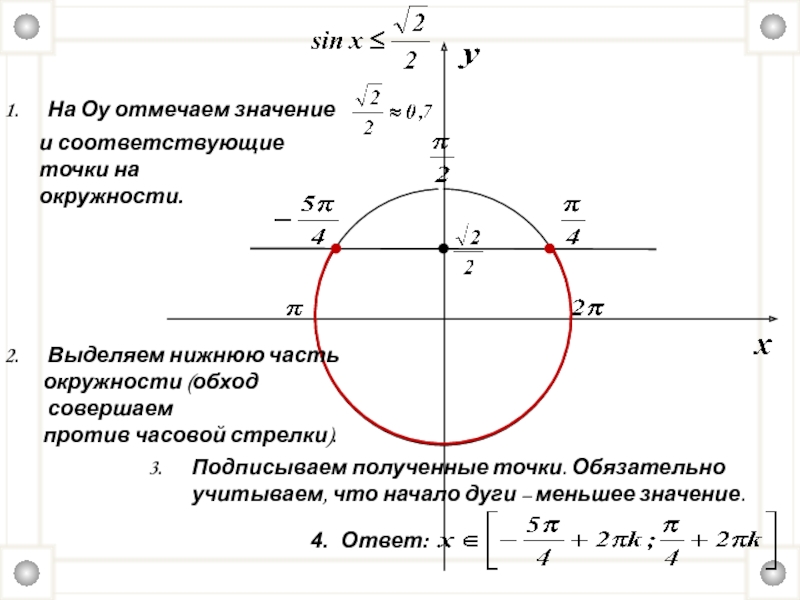
Слайд 18
На Оу отмечаем значение
и соответствующие точки на
окружности.
Выделяем нижнюю часть
окружности (обход совершаем
против часовой стрелки).
Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение.
4. Ответ:
Слайд 19
t1
Неравенство cost > a
Алгоритм решения
0
x
y
1. Отметить на оси абсцисс интервал x
2. Выделить дугу окружности, соответствующую интервалу.
3. Выбрать положительный обход дуги ( против часовой стрелки)
4 Записать числовые значения точек t1 и t2 , учитывая, что начало дуги –меньшее значение.
5. Записать общее решение неравенства.
a
-t1
-1
1
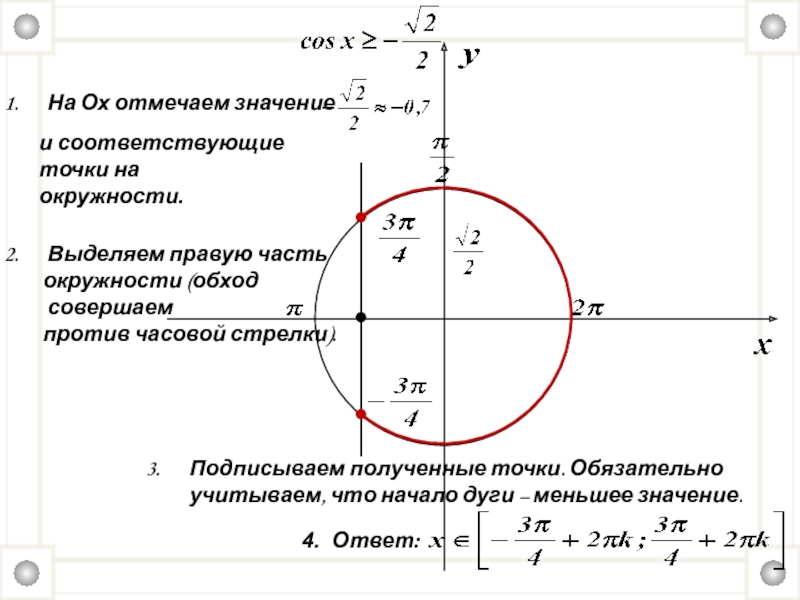
Слайд 20
На Ох отмечаем значение
и соответствующие точки на
окружности.
Выделяем правую часть
окружности (обход совершаем
против часовой стрелки).
Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение.
4. Ответ:
Слайд 21
Неравенство cost ≤ a
Алгоритм
0
x
y
1. Отметить на оси абсцисс интервал x
2. Выделить дугу окружности, соответствующую интервалу.
3. Выбрать положительный обход дуги ( против часовой стрелки)
4 Записать числовые значения точек t1 и t2 , учитывая, что начало дуги –меньшее значение.
5. Записать общее решение неравенства.
a
t1
2π-t1
-1
1
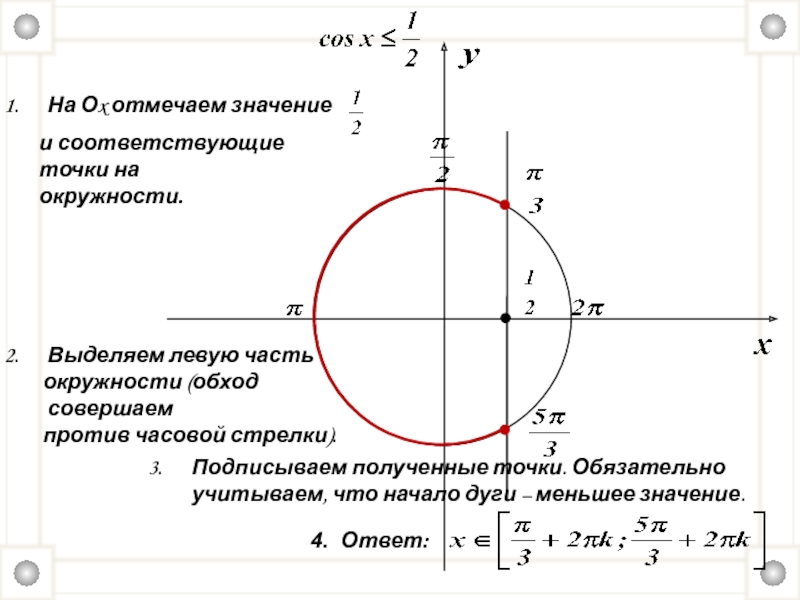
Слайд 22
На Оx отмечаем значение
и соответствующие точки на
окружности.
Выделяем левую часть
окружности (обход совершаем
против часовой стрелки).
Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение.
4. Ответ:
Слайд 23Организация изучения правила умножения десятичных дробей
Мотивационная задача:
Человек идет со скоростью
Обоснование потребности в новом правиле - принцип общности решения типовых задач: если некоторая типовая задача решается по какому-либо установленному правилу или формуле, то тем же способом должна решаться и любая другая задача, в условии которой числа заменены другими, при которых задача не теряет смысла.
Слайд 24Решение задачи:
S = v∙t
4,6∙3 = 4,6 + 4,6+4,6 = 13, 8
4,6 ∙ 0,1 = ?
За 1 час 4600 м; за 0,1 часа в 10 раз меньше, т.е.
4600 м: 10 = 460м = 0,46 км
4,6 ∙ 0,3 = ?
За 0,1 ч – 0,46 км, за 0,3 ч в 3 раза больше, т.е.
0,46∙3 = 0,46+0,46+0,46 = 1,38 (км)
Слайд 25Нельзя ли найти более простой способ умножения?
Сравним:
46∙ 3= 138
1 знак 1 знак 1 знак 1 знак 2 знака
Ориентировочная основа действий (ООД)
4,6 ∙ 0,3 =?
46 ∙ 3 = 138
4,6 0,3
1 знак 1 знак
3. 138 1,38
(1+1) знака
Ответ: 4,6 ∙ 0,3 = 1,38
Слайд 26Оперирование в режиме пошагового контроля
0,3 ∙ 1,08 =
2,301 ∙ 12, 02
Постепенное снятие контроля
2703
х 24
10812
5406
64872
2,703 \ 3 знака
х 0,24 \2 знака
10812
5406
0, 64872
(3+2) =5 знаков
3. 2,703 ∙ 0,24 =
Слайд 27 В учебном процессе необходимо чаще практиковать перевод учебного теоретического материала на
Умение учащихся оформить свои рассуждения и весь ход решения задачи в виде таблицы или блок-схемы существенно дисциплинирует мышление, становится необходимым практическим качеством, способствует более быстрому и сознательному овладению алгоритмическим языком в будущем.