- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Математические парадоксы и софизмы
Содержание
- 1. Математические парадоксы и софизмы
- 2. Цель: изучить данную тему Задачи:Дать определение
- 3. Математический софизм – удивительное утверждение, в доказательстве
- 4. Парадокс (греч. "пара" - "против", "докса" -
- 5. В Греции софистами
- 6. арифметическиегеометрическиеалгебраическиеВ своей работе я рассмотрелмного математических софизмови сейчас приведу примерынекоторых из них.
- 7. Алгебраические софизмы. Алгебра — один из
- 8. Слайд 8
- 9. «Уравнение x-a=0 не имеет корней»
- 10. «Все числа
- 11. Арифметика
- 12. «Дважды два - пять» Напишем
- 13. «Пять равно шести»
- 14. «Один рубль не равен ста
- 15. «Один рубль не равен ста копейкам»Где ошибка?
- 16. Геометрические софизмы
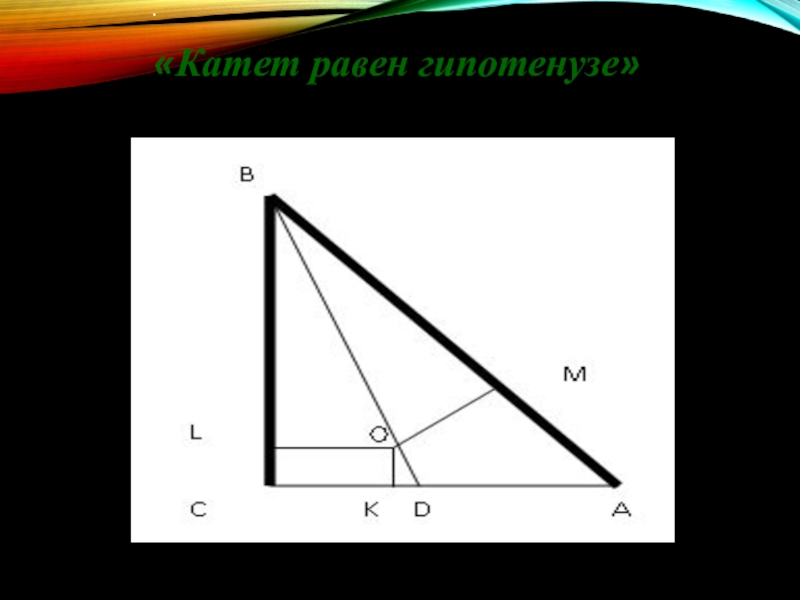
- 17. .«Катет равен гипотенузе»
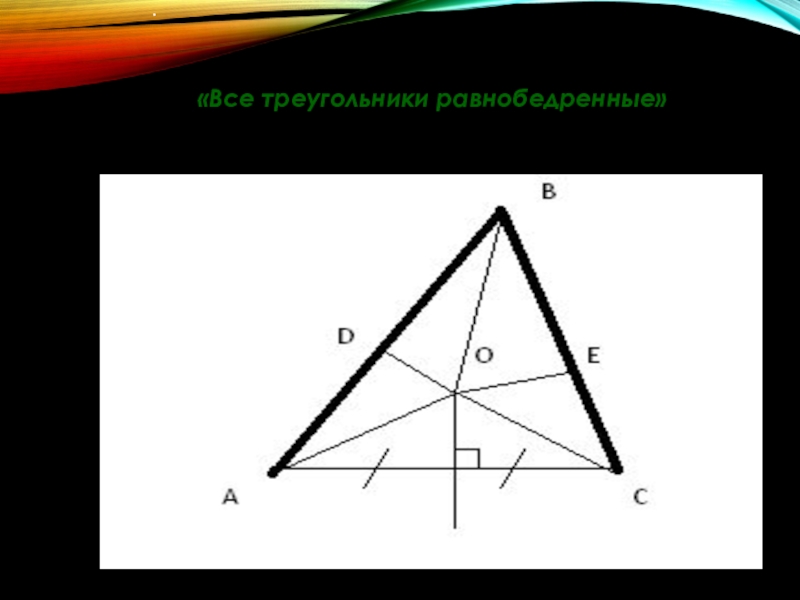
- 18. «Все треугольники равнобедренные» .
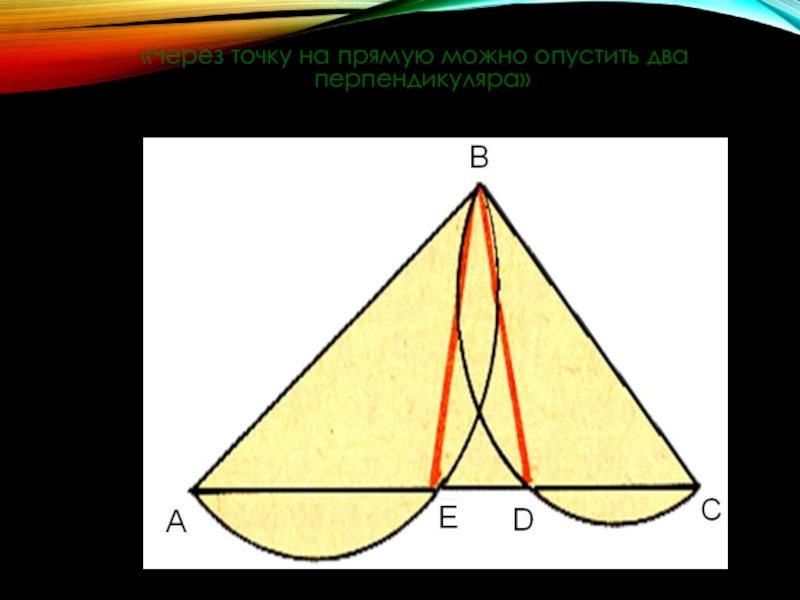
- 19. «Через точку на прямую можно опустить два перпендикуляра»
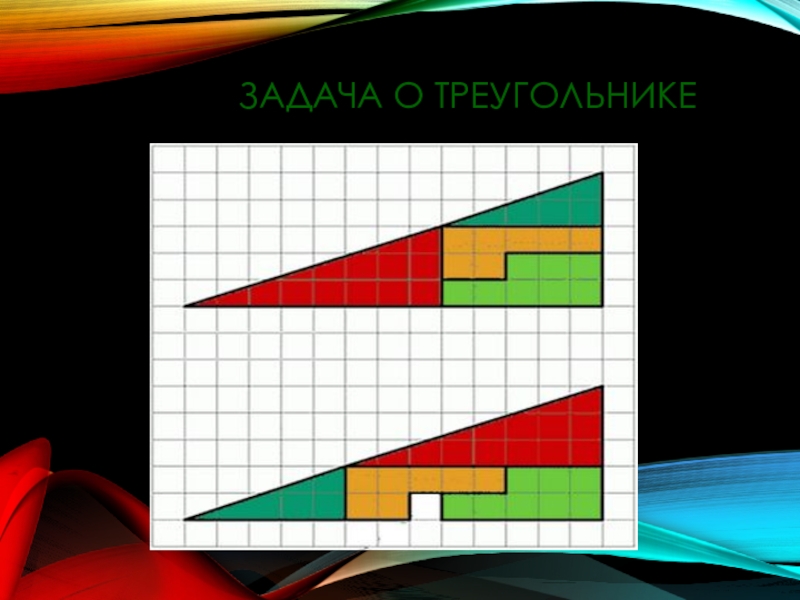
- 20. Задача о треугольнике
- 21. Парадокс «Разность квадратов»1)
- 22. Парадокс «Закономерность»Какое число следующее?1, 1, 2, 3,
- 23. Заключение Я познакомился с увлекательной темой,
- 24. Литература 1. Lietzman
- 25. Спасибо за внимание !
Цель: изучить данную тему Задачи:Дать определение понятиям «софизм» и «парадоксы»; узнать, в чем их отличие. Классифицировать различные виды софизмов и парадоксов.Понять, как найти в них ошибку.
Слайд 1Математические парадоксы и софизмы
Работу выполнил
Ученик 10 а класса
МОУ «СОШ№61»
Сегеда Михаил
Руководитель:
Учитель математики
Виноградова С.А.
Слайд 2
Цель: изучить данную тему
Задачи:
Дать определение понятиям «софизм» и «парадоксы»; узнать,
в чем их отличие.
Классифицировать различные виды софизмов и парадоксов.
Понять, как найти в них ошибку.
Классифицировать различные виды софизмов и парадоксов.
Понять, как найти в них ошибку.
Слайд 3Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а
подчас и довольно тонкие ошибки.
Особенно часто в софизмах выполняют "запрещенные" действия или не учитываются условия применимости теорем, формул и правил.
Особенно часто в софизмах выполняют "запрещенные" действия или не учитываются условия применимости теорем, формул и правил.
Математические софизмы
Софизм- формально кажущееся правильным, но по существу ложное умозаключение, основанное на неправильном подборе исходных положений (словарь Ожегова)
Слайд 4 Парадокс (греч. "пара" - "против", "докса" - "мнение") близок к софизму.
Но от него он отличается тем, что это не преднамеренно полученный противоречивый результат.
Парадокс - странное, расходящееся с общепринятым мнением, высказывание, а также мнение, противоречащее (иногда только на первый взгляд) здравому смыслу (словарь Ожегова).
Математический парадокс – высказывание, которое может быть доказано и как истинна, и как ложь.
Парадокс - странное, расходящееся с общепринятым мнением, высказывание, а также мнение, противоречащее (иногда только на первый взгляд) здравому смыслу (словарь Ожегова).
Математический парадокс – высказывание, которое может быть доказано и как истинна, и как ложь.
Парадоксы
Слайд 5 В Греции софистами называли и простых ораторов-
философов-учителей, задачей которых было научить своих учеников «мыслить, говорить и делать».
Их задачей обычно было научить убедительно защитить любую точку зрения.
Парадоксы были типичными способами постановки вопроса в античном мышлении. За свою историю математика испытала три сильнейших потрясения, три кризиса, которые касались ее основ. И все три сопровождались обнаружением парадоксов.
Их задачей обычно было научить убедительно защитить любую точку зрения.
Парадоксы были типичными способами постановки вопроса в античном мышлении. За свою историю математика испытала три сильнейших потрясения, три кризиса, которые касались ее основ. И все три сопровождались обнаружением парадоксов.
А теперь немного истории…
Слайд 6арифметические
геометрические
алгебраические
В своей работе я рассмотрел
много математических софизмов
и сейчас приведу примеры
некоторых из
них.
Слайд 7Алгебраические софизмы.
Алгебра — один из больших разделов математики,
принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.
Слайд 9
«Уравнение x-a=0 не имеет корней»
Дано уравнение x-a=0. Разделив
обе части этого уравнения на x-a, получим, что 1=0. Поскольку это равенство неверное, то это означает, что исходное уравнение не имеет корней.
Где ошибка?
Поскольку x=a – корень уравнения, то, разделив на выражение x-a обе его части, мы потеряли этот корень и поэтому получили неверное равенство 1=0.
Где ошибка?
Поскольку x=a – корень уравнения, то, разделив на выражение x-a обе его части, мы потеряли этот корень и поэтому получили неверное равенство 1=0.
Слайд 10
«Все числа равны между собой»
.
возьмём
числа a < b,
тогда существует такое c > 0, что: a + c = b
умножим обе части на (a − b), имеем: (a + c)(a − b) = b(a − b)
a2 + ca − ab − cb = ba − b2
cb переносим вправо, имеем:
a2 + ca − ab = ba − b2 + cb
a(a + c − b) = b(a − b + c) отсюда a = b
Где ошибка?
По определению : a + c = b
Значит, a + c − b = 0
И выражение a(a + c − b) = b(a + c − b)
Тождественно a ∙ 0 = b ∙ 0.
тогда существует такое c > 0, что: a + c = b
умножим обе части на (a − b), имеем: (a + c)(a − b) = b(a − b)
a2 + ca − ab − cb = ba − b2
cb переносим вправо, имеем:
a2 + ca − ab = ba − b2 + cb
a(a + c − b) = b(a − b + c) отсюда a = b
Где ошибка?
По определению : a + c = b
Значит, a + c − b = 0
И выражение a(a + c − b) = b(a + c − b)
Тождественно a ∙ 0 = b ∙ 0.
Слайд 11
Арифметика - (греч. arithmetika, от arithmys — число), наука о
числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними. Так что же такое арифметические софизмы?
Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
Слайд 12 «Дважды два - пять»
Напишем тождество 4:4=5:5.
Вынесем
из каждой части тождества общие
множители за скобки, получаем: 4(1:1)=5(1:1) или
Так как 1:1=1, то сократим и получим
Где ошибка?
Ошибка сделана при вынесении общих множителей 4 из левой части и 5 из правой. Действительно, 4:4=1:1, но 4:4≠4(1:1).
множители за скобки, получаем: 4(1:1)=5(1:1) или
Так как 1:1=1, то сократим и получим
Где ошибка?
Ошибка сделана при вынесении общих множителей 4 из левой части и 5 из правой. Действительно, 4:4=1:1, но 4:4≠4(1:1).
Слайд 13 «Пять равно шести»
Возьмем тождество 35+10-45=42+12-54.
В каждой части вынесем за скобки общий множитель:
5(7+2-9)=6(7+2-9).
Теперь, получим, что 5=6.
Где ошибка?
Ошибка допущена при делении верного равенства 5(7+2-9)=6(7+2-9) на число
7+2-9, равное 0. Этого нельзя делать.
Любое равенство можно делить только на число, отличное от 0.
5(7+2-9)=6(7+2-9).
Теперь, получим, что 5=6.
Где ошибка?
Ошибка допущена при делении верного равенства 5(7+2-9)=6(7+2-9) на число
7+2-9, равное 0. Этого нельзя делать.
Любое равенство можно делить только на число, отличное от 0.
Слайд 14
«Один рубль не равен ста копейкам»
Известно, что любые
два равенства можно перемножить почленно, не нарушая при этом равенства, т. е.если
а = b и c = d, то ac = bd.
Применим это положение к двум очевидным равенствам: 1 рубль = 100 копейкам и
10 рублей = 1000 копеек
Перемножая эти равенства почленно, получим
10 рублей = 100 000 копеек
и разделив последнее равенство на 10, получим, что
1 рубль = 10 000 копеек
Таким образом,
один рубль не равен ста копейкам.
а = b и c = d, то ac = bd.
Применим это положение к двум очевидным равенствам: 1 рубль = 100 копейкам и
10 рублей = 1000 копеек
Перемножая эти равенства почленно, получим
10 рублей = 100 000 копеек
и разделив последнее равенство на 10, получим, что
1 рубль = 10 000 копеек
Таким образом,
один рубль не равен ста копейкам.
Слайд 15«Один рубль не равен ста копейкам»
Где ошибка?
Ошибка, допущенная в этом
софизме, состоит в нарушении правила действий с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.
Слайд 16Геометрические софизмы
Это умозаключения
или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или противоречивое утверждение, связанное с геометрическими фигурами и действиями над ними
Слайд 21 Парадокс «Разность квадратов»
1) а²-а² = а²-а² -
имеем равенство
2) а(а-а) = (а+а)(а-а) – в первой части вынесем общий множитель за скобки, а во второй воспользуемся формулой
3) а = а+а – сократим на общий множитель (а-а)
4) а = 2а.
2) а(а-а) = (а+а)(а-а) – в первой части вынесем общий множитель за скобки, а во второй воспользуемся формулой
3) а = а+а – сократим на общий множитель (а-а)
4) а = 2а.
Слайд 22Парадокс «Закономерность»
Какое число следующее?
1, 1, 2, 3, 5, 8, 13, 21,
34, 55, 89, ...
Ответ: 144, т.к.
данный ряд является числами Фибоначчи, где каждое число – сумма двух предыдущих.
Ответ: 144, т.к.
данный ряд является числами Фибоначчи, где каждое число – сумма двух предыдущих.
Слайд 23Заключение
Я познакомился с увлекательной темой, узнал много нового, научился
решать задачки на софизмы, находить в них ошибку, разбираться в парадоксах.
Тема моей работы далеко не исчерпана. Я рассмотрел лишь некоторые, самые известные примеры софизмов и парадоксов. На самом деле их намного больше.
Развитая логика мышления поможет не только в решении каких-нибудь математических задач, но еще может пригодиться в жизни.
Тема моей работы далеко не исчерпана. Я рассмотрел лишь некоторые, самые известные примеры софизмов и парадоксов. На самом деле их намного больше.
Развитая логика мышления поможет не только в решении каких-нибудь математических задач, но еще может пригодиться в жизни.
Слайд 24Литература
1. Lietzman W. Wo steckt der Fehler? Mathematische Trugschlüsse
und Warnzeichen. – Leipzig? 1952
2. Аменицкий Н. Математические развлечения и любопытные приемы мышления. – М., 1912
3. Богомолов С. А. Актуальная бесконечность. – М.; Л., 1934
4. Больцано Б. Парадоксы бесконечного. – Одесса, 1911
5. Брадис В. М., Харчева А. К. Ошибки в математических рассуждениях. – М., 1938
6. Горячев Д. Н., Воронец А. М. Задачи, вопросы и софизмы для любителей математики. – М., 1903
7. Литцман В., Трир Ф. Где ошибка? – СПб., 1919
8. Лямин А. А. Математические парадоксы и интересные задачи. – М., 1911
9. Мадера А.Г., Мадера Д.А. Математические софизмы. – М.: Просвещение, 2003
10. Обреимов В. И. Математические софизмы. – 2-е изд. – СПб., 1889.