- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Математическая логика
Содержание
- 1. Математическая логика
- 2. Дизъю́нкция — (лат. disjunctio - разобщение) логическая операция,
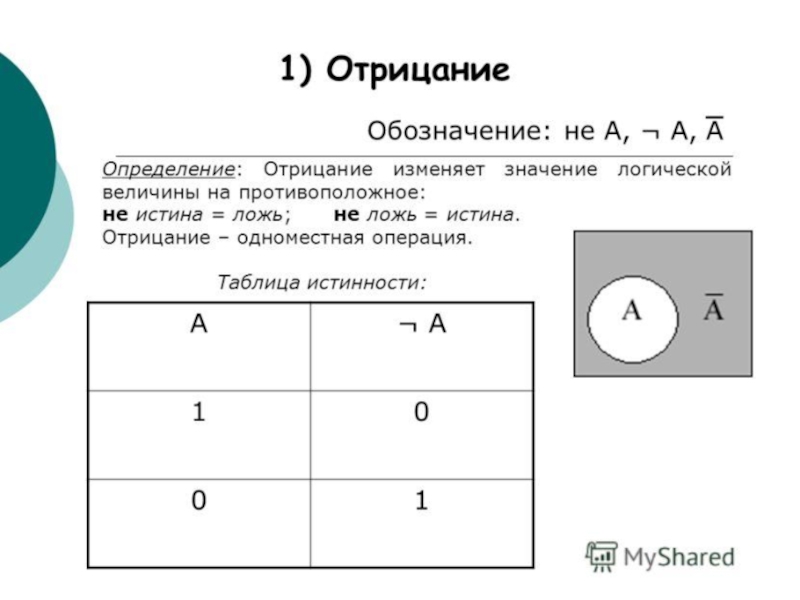
- 3. Отрицание в логике — унарная операция над
- 4. Слайд 4
- 5. Конъю́нкция (от лат. conjunctio
- 6. Слайд 6
- 7. Слайд 7
- 8. Джордж Буль 2.11.1815 – 8.12.1864
- 9. Булева алгебра.Булева алгебра Труды Буля, созданные в
- 10. Алгебра логики основывалась на трех главных операциях,
- 11. Слайд 11
Дизъю́нкция — (лат. disjunctio - разобщение) логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логи́ческое «ИЛИ», включа́ющее «ИЛИ», логическое сложе́ние, иногда просто «ИЛИ». Дизъюнкция может
Слайд 2Дизъю́нкция — (лат. disjunctio - разобщение) логическая операция, по своему применению максимально
приближённая к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логи́ческое «ИЛИ», включа́ющее «ИЛИ», логическое сложе́ние, иногда просто «ИЛИ».
Дизъюнкция может быть бинарной операцией, то есть, иметь два операнда, тернарной операцией, то есть иметь три операнда или n-арной операцией, то есть иметь n операндов.
В логике дизъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции).
Правило: результат равен 0, если все операнды равны 0; во всех остальных случаях результат равен 1.
Таблица истинности для бинарной конъюнкции:
Таблица истинности для тернарной дизъюнкции: Классическая логика
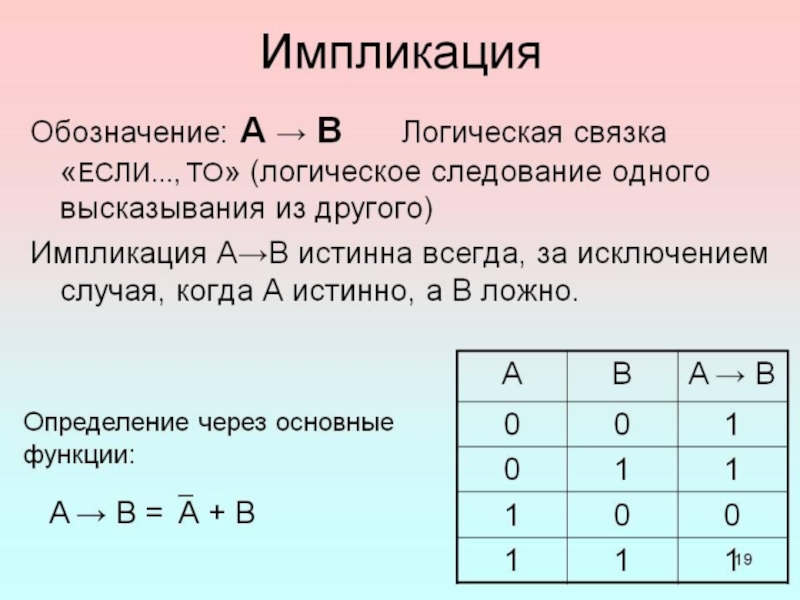
В классическом исчислении высказываний свойства дизъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства дизъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для дизъюнкции:
a → a ∨ b
b → a ∨ b
( a → c ) → ( (b → c ) → ( ( a ∨ b ) → c) )
Связь с естественным языком
Часто указывают на сходство между дизъюнкцией и союзом «или» в естественном языке, когда он употребляется в смысле «или то, или то, или оба сразу». В юридических документах часто пишут: «и/или», подразумевая «или то, или то, или оба сразу». Составное утверждение «A и/или B» считается ложным, когда ложны оба утверждения A и B, в противном случае составное утверждение истинно. Это в точности соответствует определению дизъюнкции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.
Неоднозначность естественного языка заключается в том, что союз «или» используется в двух значениях: то для обозначения дизъюнкции, то для другой операции — исключающего «ИЛИ»
Слайд 3 Отрицание в логике — унарная операция над суждениями, результатом которой является суждение
(в известном смысле) «противоположное» исходному. Обозначается знаком ¬ перед или чертой над суждением. Синоним: логическое "НЕ".
Как в классической, так и в интуиционистской логике «двойное отрицание» ¬ ¬A является следствием суждения A, то есть имеет место тавтология: A → ¬ ¬ A. Обратное утверждение ¬ ¬ A → A верно в классической логике ( закон двойного отрицания ), но не имеет места в интуиционистской. То есть, отрицание отрицания искомого утверждения не может служить интуиционистским доказательством, в отличие от классической логики. Это различие двух логических систем обычно полагается главным.
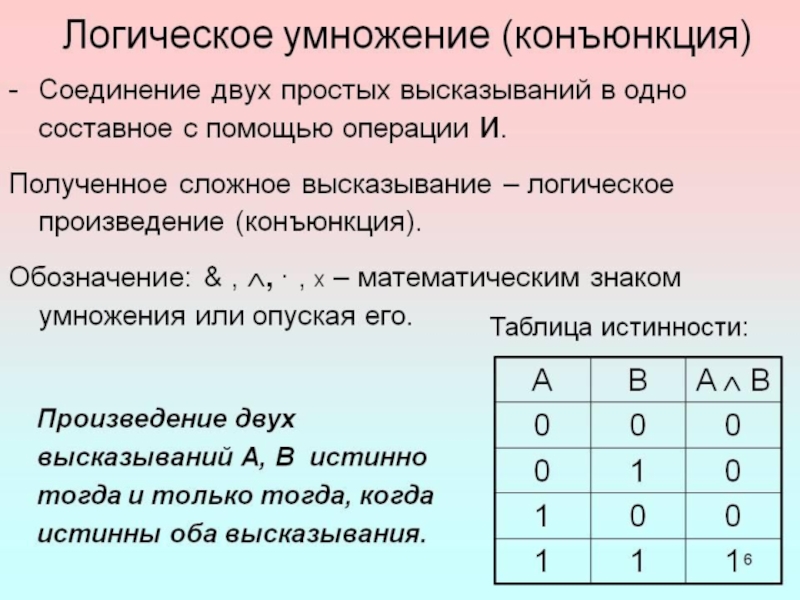
Слайд 5 Конъю́нкция (от лат. conjunctio союз, связь) — логическая
операция, по своему применению максимально приближённая к союзу "и". Синонимы: логи́ческое "И", логи́ческое умноже́ние, иногда просто "И".
Конъюнкция может быть бинарной операцией, то есть, иметь два операнда, тернарной операцией, т.е. иметь три операнда или n-арной операцией, т.е. иметь n операндов. Чаще всего встречаются следующие варианты инфиксной записи:
a & b, a ∧ b, a*b, a AND b
По аналогии с умножением в алгебре знак логического умножения может быть пропущен: ab.
Переменные могут принимать значения из множества {0,1} . Результат также принадлежит множеству {0,1}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0, 1 может использоваться любая другая пара подходящих символов, например false, true или F, T или "ложь", "истина". Правило: результат равен 1, если все операнды равны 1; во всех остальных случаях результат равен 0.
В классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции:
a∧b→a
a∧b→b
a → ( b → (a ∧ b ) )
Связь с естественным языком
Часто указывают на сходство между конъюнкцией и союзом "и" в естественном языке. Составное утверждение "A и B" считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если "истину" обозначать как 1, а "ложь" как 0. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз "и" может нести дополнительный оттенок "и тогда", "и поэтому", "и потом"..."И" также несет в себе оттенок неопределенного смысла. Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке "Мэри вышла замуж и родила ребенка" — не то же самое, что "Мэри родила ребенка и вышла замуж".
a & b, a ∧ b, a*b, a AND b
По аналогии с умножением в алгебре знак логического умножения может быть пропущен: ab.
Переменные могут принимать значения из множества {0,1} . Результат также принадлежит множеству {0,1}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0, 1 может использоваться любая другая пара подходящих символов, например false, true или F, T или "ложь", "истина". Правило: результат равен 1, если все операнды равны 1; во всех остальных случаях результат равен 0.
В классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции:
a∧b→a
a∧b→b
a → ( b → (a ∧ b ) )
Связь с естественным языком
Часто указывают на сходство между конъюнкцией и союзом "и" в естественном языке. Составное утверждение "A и B" считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если "истину" обозначать как 1, а "ложь" как 0. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз "и" может нести дополнительный оттенок "и тогда", "и поэтому", "и потом"..."И" также несет в себе оттенок неопределенного смысла. Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке "Мэри вышла замуж и родила ребенка" — не то же самое, что "Мэри родила ребенка и вышла замуж".
Слайд 9Булева алгебра.
Булева алгебра Труды Буля, созданные в 1847 и 1854 годах,
служили фундаментом алгебры логики. Математик доказал в них существование сходства между действиями логики и алгебры. Благодаря созданной Булем системе стала возможна кодировка высказываний.
Слайд 10Алгебра логики основывалась на трех главных операциях, позволяющих совершать действия с
символами и числами. Джордж питал надежды, что его система поспособствует очищению аргументов логики от словесного мусора, сделает легким и достижимым поиск верного решения.
В 1857 году Джордж Буль - математик, внесший свою лепту в развитие науки, - стал членом Королевского общества. Некоторые его труды, написанные в 1859-1860 годах и отражающие важнейшие открытия в области математики, глобально повлияли на развитие данной науки.
Несмотря на значимость в других разделах математики, алгебра логики на протяжении долгого времени расценивалась как странная. К гениям, обогнавшим свое время, относился Джордж Буль, фото изобретений ученого служат тому наглядным примером.
В 1857 году Джордж Буль - математик, внесший свою лепту в развитие науки, - стал членом Королевского общества. Некоторые его труды, написанные в 1859-1860 годах и отражающие важнейшие открытия в области математики, глобально повлияли на развитие данной науки.
Несмотря на значимость в других разделах математики, алгебра логики на протяжении долгого времени расценивалась как странная. К гениям, обогнавшим свое время, относился Джордж Буль, фото изобретений ученого служат тому наглядным примером.