- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Мастер-класс по теме Сопровождение исследовательской деятельности учащихся.
Содержание
- 1. Мастер-класс по теме Сопровождение исследовательской деятельности учащихся.
- 2. Исследование – процесс открытия или создания новых
- 3. Темы исследовательских работПрямые на решетке. Линейные уравненияРешение
- 4. Выбор конкретного объектаПрямая, проведенная на клетчатой бумаге.Площадь как метрическая характеристика многоугольника
- 5. Определение проблемыПоиск «ЦЕЛЫХ» точек прямой.Цель исследовательской работы:
- 6. Изучение литературыН.Б.Васильев, В.Л. Гутенмахер. Делимость целых
- 7. Выработка гипотезыНаличие целых точек на прямой ау
- 8. Организация и проведение экспериментаМетоды исследования:Наблюдение, экспериментирование, проведение
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
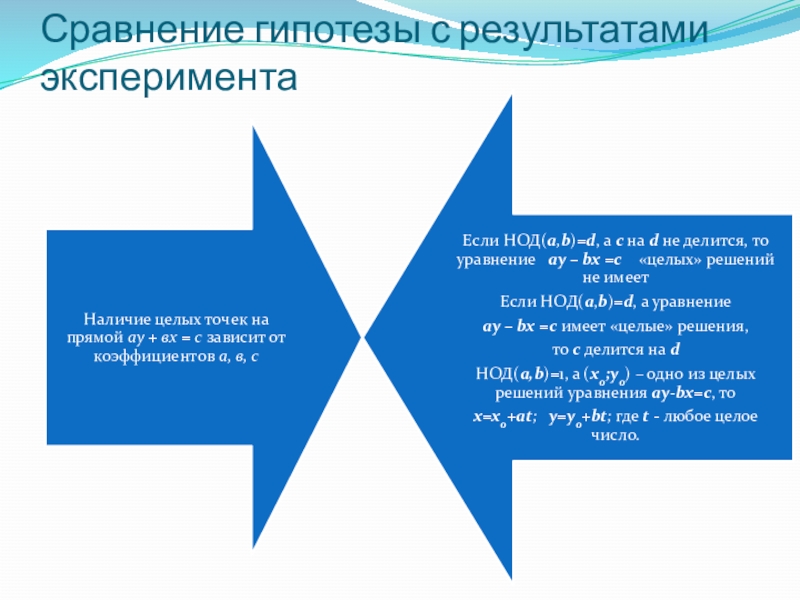
- 12. Сравнение гипотезы с результатами эксперимента
- 13. Сравнение гипотезы с результатами экспериментаВсегда можно разрезать
- 14. Формулировка выводов, основанных на экспериментальных данныхдиагональ прямоугольника
- 15. Требования к исследовательской работе:
- 16. Всякая плодотворная гипотеза кладет начало удивительному извержению потока непредвиденных открытий. Л. Бриллюзн
Слайд 1Мастер-класс по теме «Сопровождение исследовательской деятельности учащихся»
Одобеско Нина Михайловна,
учитель математики
Слайд 2Исследование – процесс открытия или создания новых знаний о мире, в
Источник истинного знания в фактах.
П. Буаст
Слайд 3Темы исследовательских работ
Прямые на решетке. Линейные уравнения
Решение линейных уравнений с двумя
Площади многоугольников
Площадь как вспомогательное средство для доказательства некоторых геометрических фактов
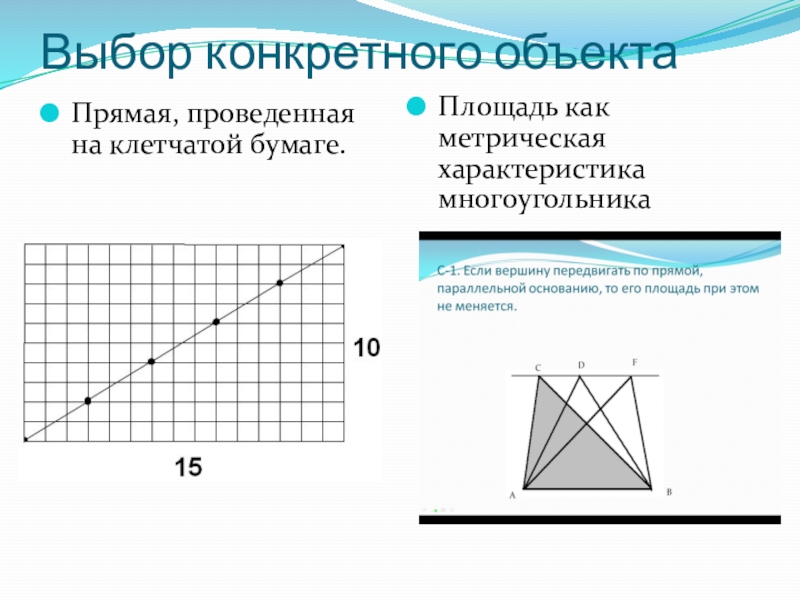
Слайд 4Выбор конкретного объекта
Прямая, проведенная на клетчатой бумаге.
Площадь как метрическая характеристика многоугольника
Слайд 5Определение проблемы
Поиск «ЦЕЛЫХ» точек прямой.
Цель исследовательской работы: разработать алгоритм решения линейного
Нахождение площади нестандартных фигур и применение площади для доказательства некоторых геометрических фактов
Цель исследовательской работы: выявить возможность применения площади для доказательства некоторых геометрических фактов
Слайд 6Изучение литературы
Н.Б.Васильев, В.Л. Гутенмахер. Делимость целых чисел. Учебное пособие для
Математическая энциклопедия: Гл. ред. И.М. Виноградов, т. 2 – М.: «Советская Энциклопедия», 1979.
Математический энциклопедический словарь./ Гл. ред. Ю.В. Прохоров; - М.: «Советская Энциклопедия», 1988.
Мордкович А.Г. Алгебра. 7кл. –М.: Мнемозина, 2003.
Колосов А.А. Книга для внеклассного чтения по математике в старших классах. – М.: Государственное учебно-педагогическое издательство, 1963.
Математика в понятиях, определениях и терминах. Часть 2 /О.В. Мантуров, Ю.К. Солнцев, Ю.И. Соркин, Н.Г. Федин. Под редакцией Л.В. Сабинина. – М.: Просвещение, 1982.
Геометрия, 7-9: учебник для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2006.
Геометрия для 8-9 классов: Учебное пособие для учащихся школ и классов с углубленным изучением математики/ А.Д. Александров, А.Л. Вернер, В.И. Рыжик. – М : Просвещение, 1991.
Площади многоугольников: Методические разработки для учащихся ОЛ «ВЗМШ» при МГУ (Н.Б. Васильев - М.: ОЛ ВЗМШ, 1996.
Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы./ И.Л. Никольская. – М.: Просвещение, 1991.
Слайд 7Выработка гипотезы
Наличие целых точек на прямой ау + вх = с
Всегда можно разрезать один из двух равновеликих многоугольников на части так, что после перекладывания получится другой
Площадь многоугольника можно использовать при доказательстве теорем
Слайд 8Организация и проведение эксперимента
Методы исследования:
Наблюдение, экспериментирование, проведение опытов;
Анализ результатов наблюдений;
Сравнение результатов
Промежуточные и итоговые обобщения, абстрагирование;
Систематизация и группировка объектов;
Создание целостной системы объектов исследования;
Конструирование новых объектов;
Проведение доказательных рассуждений
Слайд 13Сравнение гипотезы с результатами эксперимента
Всегда можно разрезать один из двух равновеликих
Площадь многоугольника можно использовать при доказательстве теорем
Многоугольники, имеющие равные площади, равновелики.
Многоугольники равносоставлены, если разрезав один можно сложить другой.
Разрезанием и складыванием невозможно изменить площадь.
Слайд 14Формулировка выводов, основанных на экспериментальных данных
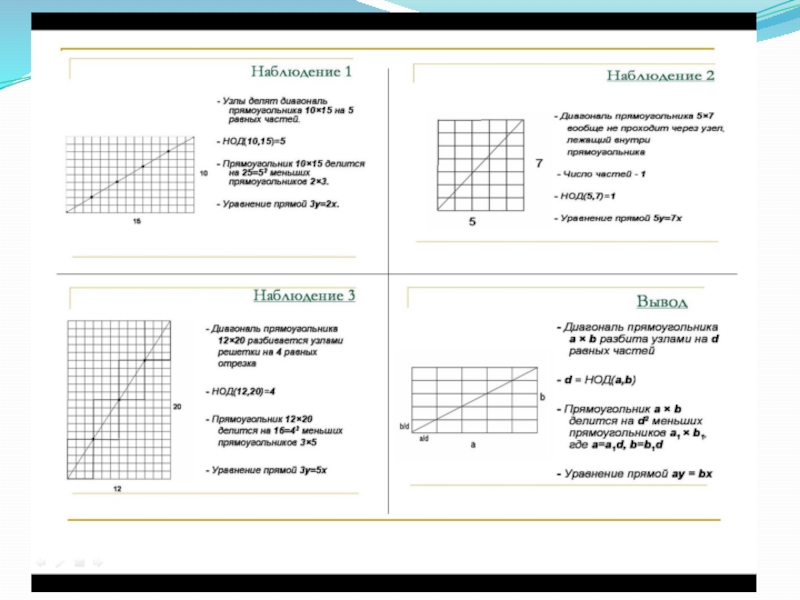
диагональ прямоугольника a×b делится узлами решетки
однородное линейное уравнение имеет бесконечное множество «целых» решений: x=at, y=bt, где t – любое целое число;
неоднородное уравнение ay – bx = с не имеет целых решений, если НОД(a,b) не является делителем с;
если НОД(a,b)=1, то уравнение ay – bx = с имеет бесконечное множество целых решений (х; у), где x=x0+at; y=y0+bt; где t - любое целое число, а (х0;у0) – одно из целых решений уравнения;
алгоритм отыскания целых положительных решений уравнения ay – bx = с можно применять при решении экономических задач.
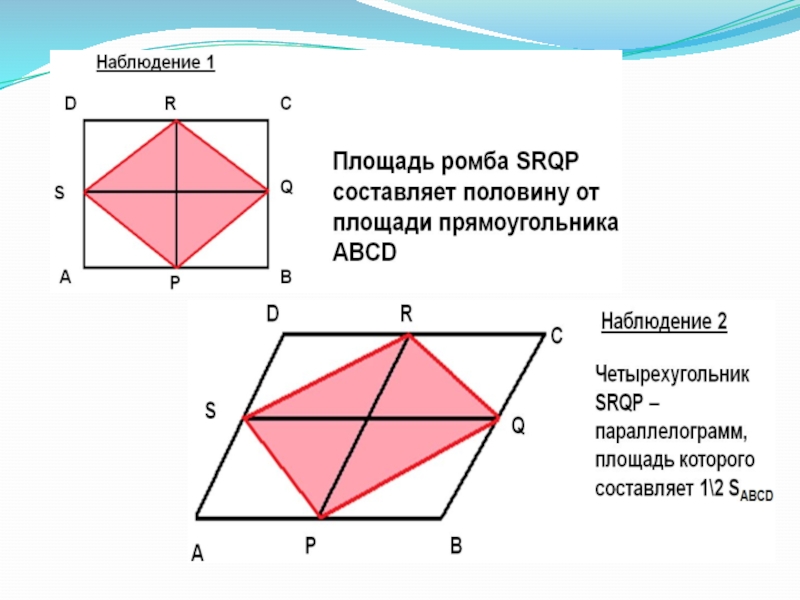
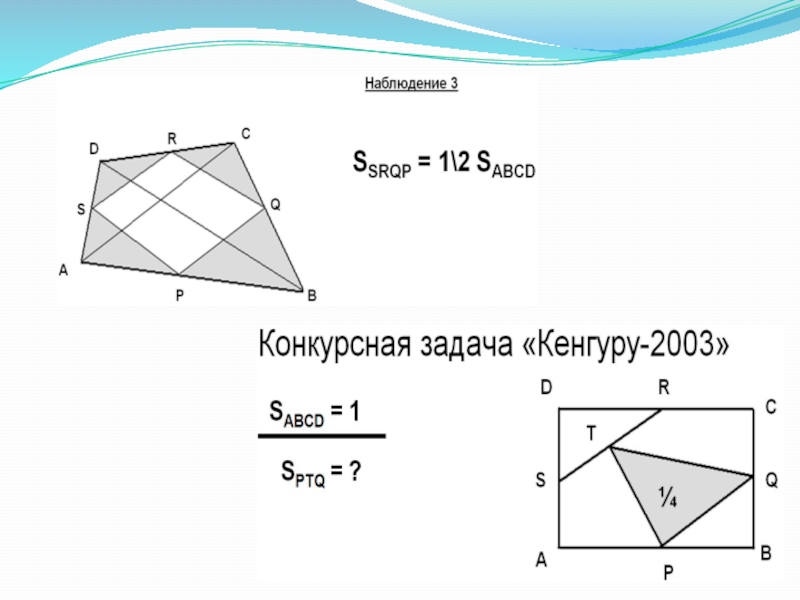
Метод «разрезания и складывания» годится для любых равных по площади многоугольников: всегда можно разрезать один из них на части так, что после перекладывания получится другой, (такие многоугольники называются равносоставленными).
Применение площади позволило доказать более рациональным способом следующие геометрические факты:
В равнобедренном треугольнике сумма расстояний от любой точки основания до боковых сторон равна высоте треугольника, опущенной на его боковую сторону.
Сумма расстояний от произвольной точки, лежащей внутри правильного треугольника или на его стороне, до его сторон равна высоте треугольника.
Треугольник, составленный из средних линий правильного треугольника, есть геометрическое место точек, расстояние от каждой из которых до одной из сторон равно сумме расстояний до двух других.
Пусть на сторонах треугольника АВС выбраны точки А1 ВС, В1 АС, С1 АВ. Тогда отрезки АА1, ВВ1 и СС1 пересекаются в одной точке тогда и только тогда, когда выполняется равенство .(теорема ЧЕВЫ)
Во всяком вписанном четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон. (теорема Птолемея)