- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Мастер класс по решению задач (6 класс)
Содержание
- 1. Мастер класс по решению задач (6 класс)
- 2. Решение задач.ЗАДАЧА
- 3. Цели урока:Развивающие: развивать
- 4. ДЕВИЗ УРОКА: «Недостаточно лишь понять
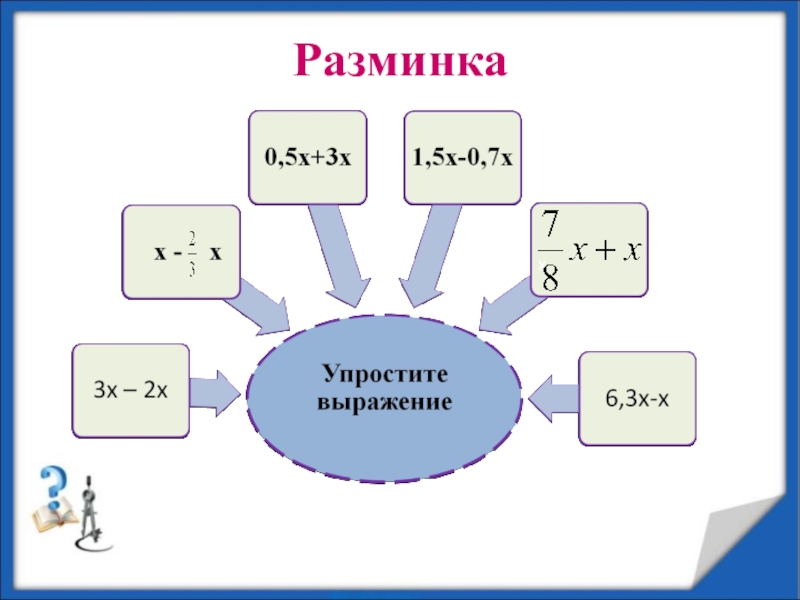
- 5. Разминка
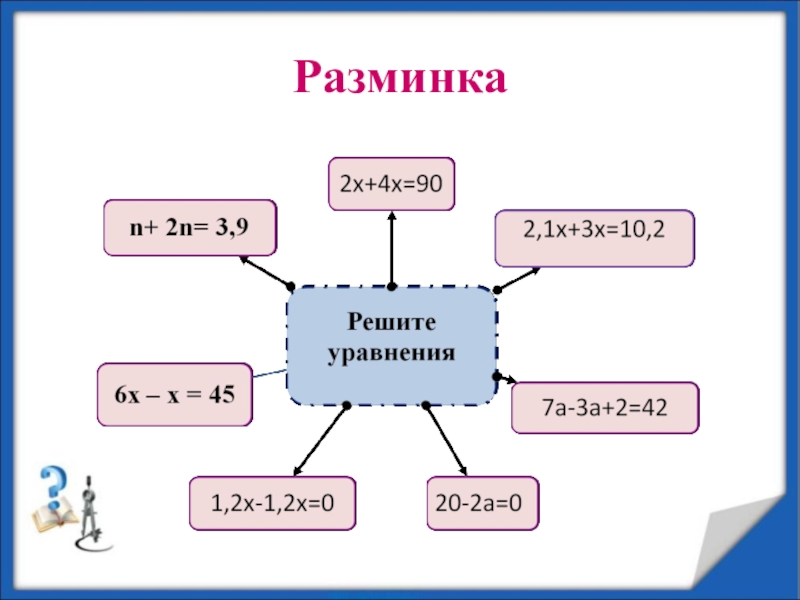
- 6. Разминка
- 7. Алгебраический (способ решения задач уравнением)Графический (рисуется чертёж)Табличный-
- 8. Классификация задач: «на движение»;
- 9. Этапы решения арифметических задач: 1. Ознакомление с
- 10. Слайд 10
- 11. ЗАДАЧА : Моторная лодка прошла
- 12. Решение задач алгебраическим способомЭтапы решения задач:1. Прочитать
- 13. Решение задач алгебраическим способомЗадача: Мама старше Ани
- 14. Пример:Задача: В шкафу стоят учебники физики и
- 15. -Реши самостоятельно:Задача:На опытном участке площадью 156 м²
- 16. Итог урокаНадо решить ещё несколько задач. Оценка
- 17. Благодарю за сотрудничество!
- 18. Дополнительная задачаЗадача: Поют в хоре и занимаются
- 19. Задача: Поют в хоре и занимаются танцами
Слайд 1МАСТЕР КЛАСС
Выполнила учитель математики
МБОУ «Шурышкарская СОШ»:
Кондыгина Валентина Романовна
Слайд 3
Цели урока:
Развивающие: развивать логическое мышление;
обучать действию по аналогии;
развивать культуру речи;
вырабатывать умение общения.
Образовательные:
познакомить учащихся с методами решения задач;
расширить кругозор учащихся.
Воспитательные:
вырабатывать умение преодолевать трудности.
Слайд 4ДЕВИЗ УРОКА:
«Недостаточно лишь понять задачу, необходимо желание решить
Пойа Д
Слайд 7Алгебраический (способ решения задач уравнением)
Графический (рисуется чертёж)
Табличный- это- решение путем занесения
Арифметический (решение задач по действиям или решение задач по вопросам)
Геометрический метод. Решить задачу геометрическим методом - значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур.
Комбинированный метод позволяет получить ответ на требование задачи более простым путем.
Метод проб и ошибок - в нем ответ на вопрос задачи угадывается. Угадывание ответа требует интуиции, без которой невозможно никакое решение
Логический метод.- это значит найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения.
способы решения задач
Слайд 8Классификация задач:
«на движение»;
«на проценты»;
«на части»; «на работу»; «на смеси и сплавы»; «на смешение и концентрацию»; «на время»; «на покупку и продажу» и т. п.
Слайд 9Этапы решения арифметических задач:
1. Ознакомление с содержанием задачи;
2. Поиск решения задачи;
3.
4. Проверка решения задачи.
Слайд 10
Решение задач
Задача: Катер проплыл по озеру за 2 часа 48 километров, а против течения реки за 2 часа он проплыл 46 километров. Какова скорость течения реки?
Возникает вопрос. С какой скоростью катер проплывет за час по озеру? Выполняется действие:
1) 48:2=24 (км/ч) скорость катера по озеру.
Возникает вопрос. С какой скоростью катер проплывет против течения реки? Выполняется действие:
2) 46:2=23 (км/ч) скорость катера против течения реки.
Раз, у нас есть скорость катера по озеру (то есть скорость катера в стоячей воде) и скорость катера против течения реки, значит, мы можем найти скорость течения реки. Выполняется действие:
3)24-23=1 (км/ч) скорость течения реки.
Пишется ответ: Ответ: 1 км/ч.
Слайд 11
ЗАДАЧА : Моторная лодка прошла 47,6 км против течения
Решение.
Решим задачу по действиям.
1. Найдем скорость по течению: 25,3+1,5=26,8 (км/ч).
2. Определим скорость против течения: 25,3 – 1,5= 23,8 (км/ч).
3. Найдем время, затраченное на путь против течения реки: 47,6:23,8=2 (ч.).
4. Время по течению: 107,2:26,8=4 (ч.).
5. Время в пути 4+2=6 (ч.).
Ответ: 6 часов.
Реши самостоятельно!
Слайд 12
Решение задач алгебраическим способом
Этапы решения задач:
1. Прочитать задачу.
2. Составить условие
3. Составить уравнение по данным в задаче.
4. Решить уравнение и найти все неизвестные.
5. Записать ответ
Слайд 13
Решение задач алгебраическим способом
Задача: Мама старше Ани в 5 раз, а
Пишем: Пусть х возраст Ани, тогда 5х возраст мамы и 9х возраст бабушки. Зная, что им вместе 90 лет составим и решим уравнение: 1) х+5х+9х=90
15х=90
х=90:15
х=6(лет) Ане
Зная, что возраст мамы в 5 раз больше возраста Ани, выполняем действие: 2) 6*5=30 (лет) возраст мамы
Зная, что возраст бабушки в 9 раз больше возраста Ани, выполняем действие:
2) 6*9=54 (года) возраст бабушки.
Ответ: 6 лет Ане, 30 лет Маме и 54 года бабушке.
Слайд 14Пример:
Задача: В шкафу стоят учебники физики и учебники химии – всего 112
Решение: Пусть х будет учебников физики, тогда х учебников химии. Всего учебников 112. Составим и решим уравнение:
х + х = 112
Значит 72 учебника по физике, то 112-72=40 учебников по химии.
Ответ: 72, 40.
Слайд 15-
Реши самостоятельно:
Задача:На опытном участке площадью 156 м² посадили картофель и капусту,
Решение: Пусть х м² площадь участка под капустой, тогда 3х м² площадь участка под картофелем. Т.к. площадь участка под капустой и картофелем равна 156 м², составим уравнение:
2) х + 3х = 156
4х =156
х = 156 : 4
х = 39 (м²) занимает капуста,
2) 39 · 3 = 117(м²) занимает картофель.
Ответ: 39м²; 117 м²
Слайд 16Итог урока
Надо решить ещё несколько задач. Оценка 4
Я – молодец!
У меня
Ох, сколько ещё надо решать! Оценка 3
Слайд 18
Дополнительная задача
Задача: Поют в хоре и занимаются танцами 82 студента, занимаются
Решение.
1-й способ.
1) 82 + 32 + 78 = 192 (чел.) - удвоенное число студентов, поющих в хоре, занимающихся танцами и художественной гимнастикой;
2) 192 : 2 = 96 (чел.) - поют в хоре, занимаются танцами и художественной гимнастикой;
3) 96 – 32 = 64 (чел.) - поют в хоре;
4) 96 – 78 = 18 (чел.) - занимаются танцами;
5) 96 – 82 = 14 (чел.) - занимаются художественной гимнастикой. Ответ: 64 студента поют в хоре, 14 студентов занимаются художественной гимнастикой, 18 студентов занимаются танцами.
Слайд 19
Задача: Поют в хоре и занимаются танцами 82 студента, занимаются танцами
2-й способ.
1) 82 – 32 = 50 (чел.) - настолько больше студентов поют в хоре, чем
занимаются художественной гимнастикой;
2) 50 + 78 = 128 (чел.) - удвоенное число студентов, поющих в хоре;
3) 128 : 2 = 64 (чел.) - поют в хоре;
4) 78 – 64 = 14 (чел.) — занимаются художественной гимнастикой;
5) 82 – 64 = 18 (чел.) - занимаются танцами.
Ответ: 64 студента поют в хоре, 14 студентов занимаются художественной гимнастикой, 18 студентов занимаются танцами.