- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Конструирование урока по теме Признаки параллелограмма
Содержание
- 1. Конструирование урока по теме Признаки параллелограмма
- 2. Цели урока:активизировать различные каналы восприятия, способствовать повышению
- 3. Содержание темы. Данная тема «Признаки параллелограмма» изучается
- 4. Методические требования. Научность - знание системы принципов
- 5. Хоть стороны мои Попарно и равны,И параллельны,
- 6. Признаки параллелограммаМногоугольникиЧетырехугольникиНевыпуклыеВыпуклыеПараллелограммПрямоугольникКвадратРомб
- 7. Определение.Параллелограммом называется четырехугольник, у которого противолежащие
- 8. Признаки параллелограммаПризнак 1. Если в четырехугольнике две
- 9. Признак 1. Если в четырехугольнике две
- 10. Признаки параллелограммаDСВА12Признак 2. Если в четырехугольнике
- 11. Признаки параллелограммаВАСDO3124Признак 3. Если в четырехугольнике
- 12. Ключевые задачиВАСDДано: АВСD – четырехугольник
- 13. Задачи по темеВ параллелограмме MNPQ, точки A
- 14. Дано: NBFD параллелограмм. Доказать: ABCD параллелограмм.В параллелограмме
- 15. Задачи по темеВ параллелограмме ABCD проведена биссектриса
- 16. Точки М и К являются соответственно серединами
- 17. ЛитератураЛ. С. Атанасян, В. Ф. Бутузов и
Слайд 1Конструирование урока
по теме «Признаки параллелограмма»
Выполнила: Рыбакова Е.А.
МБОУ «Лицей» г.Протвино
Слайд 2Цели урока:
активизировать различные каналы восприятия, способствовать повышению внимания учащихся на уроке;
способствовать
формировать навыки осмысленного запоминания теорем;
развивать пространственное воображение учащихся, образное мышление;
совершенствовать графическую культуру;
обогатить урок эмоциональной окрашенностью.
Задачи урока:
Образовательные:
Повторить и расширить знания учащихся о свойствах и признаках параллелограмма;
Сформировать умения применять изученные признаки при решении задач;
Воспитательные:
Направлены на формирование положительной мотивации учения,
Воспитание самостоятельности и коллективизма;
Развивающие:
Развивать познавательные процессы, память, воображение, мышление, внимание.
Слайд 3Содержание темы.
Данная тема «Признаки параллелограмма» изучается в курсе геометрии 8
Слайд 4Методические требования.
Научность - знание системы принципов дидактики, их иерархии, взаимосвязей
Доступность - безусловный учет обученности, обучаемости, учебных и воспитательных возможностей учащихся разных возрастов, классов, групп; учет особенностей, интересов, склонностей, запросов учащихся.
Межпредметные связи - формирования у учащихся целостного представления о системе знаний, о мире и с целью развития эрудиции школьников, а при необходимости и специальное осуществление учителем межпредметной координации учебного материала.
Мотивация - активно использовать методы развития познавательного интереса и постоянно поддерживать этот интерес.
Гибкость - четкое следование замыслу плана урока и одновременная готовность (и умение) гибко перестраивать его ход при изменении учебных ситуаций, умение переходить к реализации запасных методических вариантов, предварительное продумывание которых должно превратиться в привычку.
Рефлексия - регулярный анализ полученных на уроке (или системе уроков) результатов обучения, воспитания, развития школьников.
Слайд 5Хоть стороны мои
Попарно и равны,
И параллельны,
Все ж я в
Что не равны мои диагонали,
Да и углы они не делят пополам.
А кто я, догадайся сам.
Параллелограмм
Признаки параллелограмма
Слайд 6
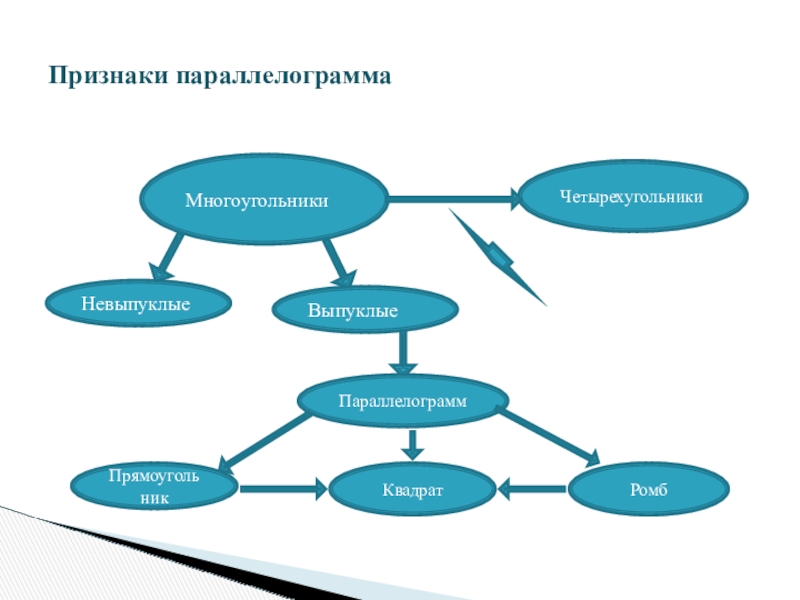
Признаки параллелограмма
Многоугольники
Четырехугольники
Невыпуклые
Выпуклые
Параллелограмм
Прямоугольник
Квадрат
Ромб
Слайд 7 Определение.
Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.
АВ
BC || AD
Признаки параллелограмма
Свойства параллелограмма.
Свойство 1. В параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.
Слайд 8Признаки параллелограмма
Признак 1. Если в четырехугольнике две стороны параллельны и равны,
Признак 2. Если в четырехугольнике противолежащие стороны попарно равны, то этот четырехугольник – параллелограмм.
Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
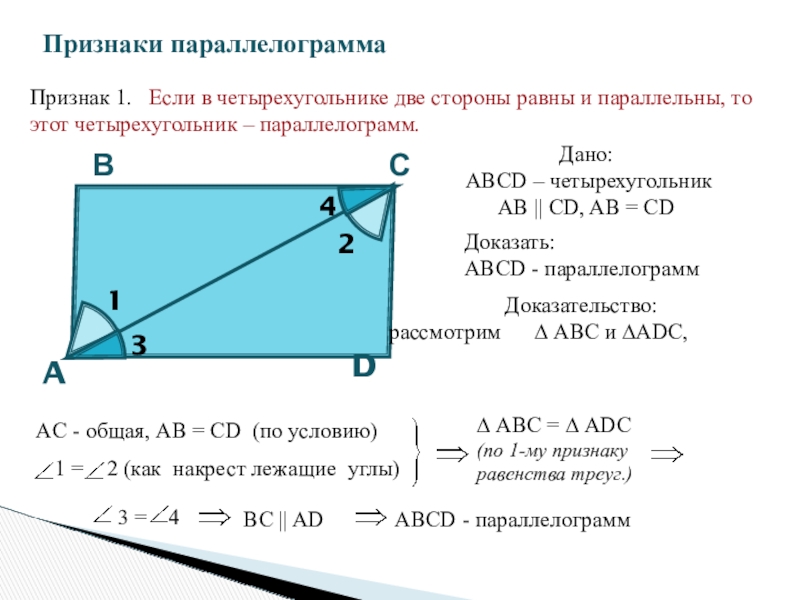
Слайд 9Признак 1. Если в четырехугольнике две стороны равны и параллельны,
Признаки параллелограмма
A
С
В
D
2
1
4
3
Дано:
АВСD – четырехугольник
AB || CD, AB = CD
Доказать:
АВСD - параллелограмм
Доказательство:
рассмотрим ∆ АВС и ∆ADC,
AC - общая, AB = CD (по условию)
1 = 2 (как накрест лежащие углы)
∆ АВС = ∆ ADC
(по 1-му признаку
равенства треуг.)
3 = 4
BC || AD
АВСD - параллелограмм
Слайд 10Признаки параллелограмма
D
С
В
А
1
2
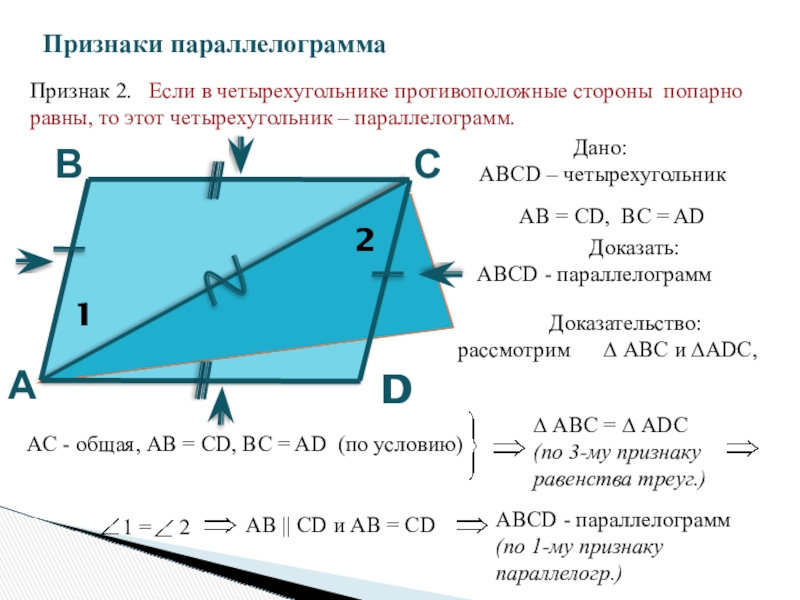
Признак 2. Если в четырехугольнике противоположные стороны попарно равны,
Дано:
АВСD – четырехугольник
Доказать:
АВСD - параллелограмм
Доказательство:
рассмотрим ∆ АВС и ∆ADC,
AB = CD, BC = AD
AC - общая, AB = CD, BC = AD (по условию)
∆ АВС = ∆ ADC
(по 3-му признаку
равенства треуг.)
1 = 2
AB || CD и AB = CD
АВСD - параллелограмм
(по 1-му признаку параллелогр.)
Слайд 11Признаки параллелограмма
В
А
С
D
O
3
1
2
4
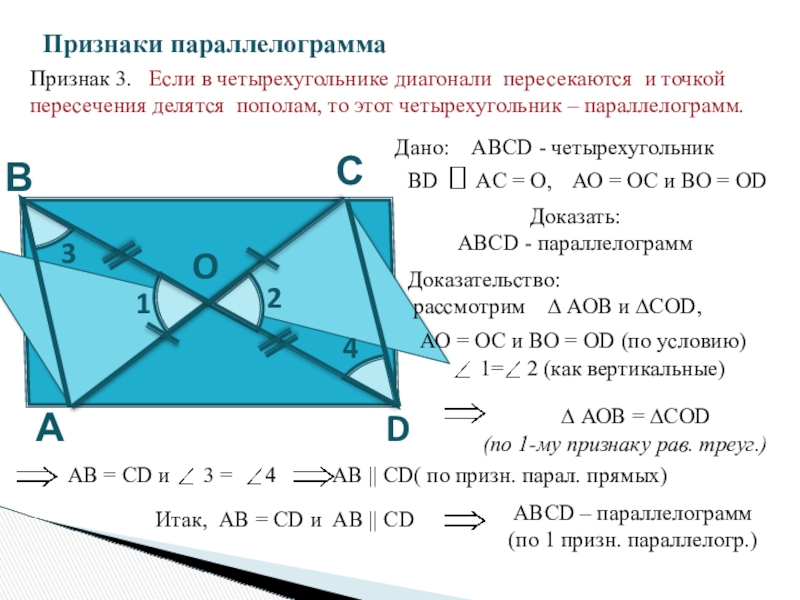
Признак 3. Если в четырехугольнике диагонали пересекаются и точкой
Дано: АВСD - четырехугольник
ВD AC = O,
Доказать:
ABCD - параллелограмм
Доказательство:
рассмотрим ∆ АОВ и ∆СОD,
АО = ОС и ВО = ОD
АО = ОС и ВО = ОD (по условию)
1= 2 (как вертикальные)
АВ = СD и 3 = 4
∆ АОВ = ∆СОD
(по 1-му признаку рав. треуг.)
АВ || СD( по призн. парал. прямых)
Итак, АВ = СD и АВ || СD
ABCD – параллелограмм
(по 1 призн. параллелогр.)
Слайд 12
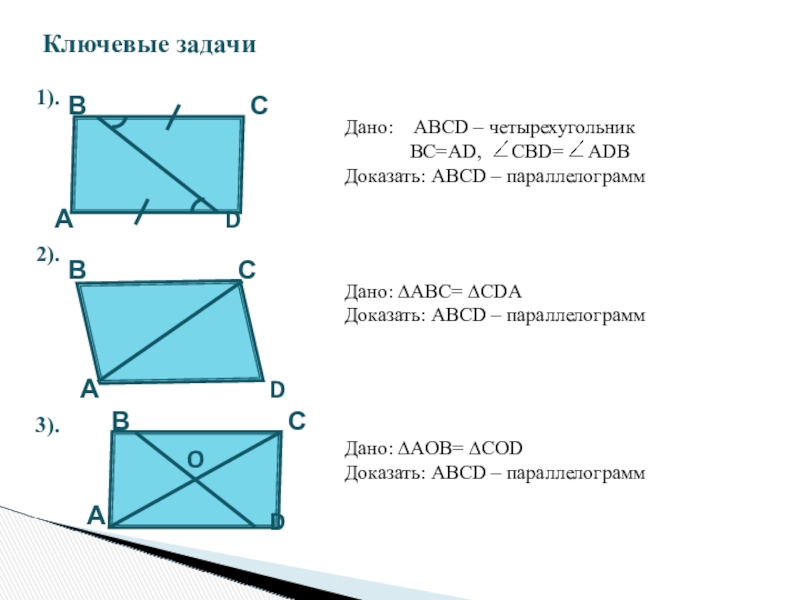
Ключевые задачи
В
А
С
D
Дано: АВСD – четырехугольник
Доказать: ABCD – параллелограмм
1).
2).
В
А
С
D
Дано: ∆ABC= ∆CDA
Доказать: ABCD – параллелограмм
3).
В
С
А
D
O
Дано: ∆AOВ= ∆COD
Доказать: ABCD – параллелограмм
Слайд 13Задачи по теме
В параллелограмме MNPQ, точки A и B середины сторон
В параллелограмме ABCD на сторонах AB и CD отложены равные отрезки BM и DN соответственно. Докажите, что AМСN параллелограмм.
В параллелограмме KCEA на диагонали KE отложены равные отрезки KB и ED. Докажите, что ABCD параллелограмм.
На продолжении противоположных сторон AB и CD параллелограмма отложены равные отрезки BM и DN. Определите вид четырехугольника AMCN.
Докажите, что середины сторон параллелограмма являются вершинами другого параллелограмма. Найдите периметр полученного параллелограмма, если диагонали данного 12 см и 8 см.
Слайд 14Дано: NBFD параллелограмм.
Доказать: ABCD параллелограмм.
В параллелограмме ABCD биссектрисы тупых углов
Радиусы ОА и МВ двух одинаковых колес тепловоза равны между собой. Стержень АВ, длина которого равна расстоянию ОМ между центрами колес, передает движение от одного колеса к другому. Докажите, что отрезки АВ и ОМ либо параллельны, либо лежат на одной прямой.
В треугольнике МРК М=65⁰. На сторонах МК, МР, РК отмечены точки А, В, С, соответственно так , что середина стороны РК-точка С, АМ=КС, ВР=АС, ВАМ=50⁰ .Докажите ,что СРВ+ АВР =180⁰.
Дан равнобедренный треугольник АВС с основанием АС. На сторонах АВ, ВС, АС отмечены точки D , Е, Р соответственно так, что отрезки АЕ и DР имеют общую середину. Докажите, что DЕР= ВСА.
Задачи по теме
В
N
D
F
С
A
Слайд 15Задачи по теме
В параллелограмме ABCD проведена биссектриса угла A , которая
В выпуклом четырехугольнике АВС D,точки М , N , Р ,Q середины сторон АВ, ВС, СD и АD соответственно. Определите вид четырехугольника МNРQ и найдите периметр , если диагонали имеют длины 14 см. и 18 см.
На сторонах ВС и А D выпуклого четырехугольника АВСD соответственно взяты точки М и К так , что пары отрезков АМ и ВК , КС и МD имеют общие середины. Докажите ,что ВАD= ВСD .
В параллелограмме АВСD диагонали пересекаются в точке О , причем СОВ=126 ⁰, САD =28 ⁰ и длина отрезка ВD вдвое больше стороны АВ. Найдите D параллелограмма.
На сторонах ВС и А D выпуклого четырехугольника АВСD отмечены точки К и Р соответственно . Диагональ BD пересекает отрезок РС в точке Е , а отрезок АК- в точке Т. Известно , что КС=АР , АТ= ЕС , ТК=ЕР. Докажите ,что АВС= АDC.
Слайд 16Точки М и К являются соответственно серединами сторон АВ и ВС
Задачи по теме
Слайд 17Литература
Л. С. Атанасян, В. Ф. Бутузов и др. «Геометрия 7-9»
Б.Г. Зив,
П.И. Алтынов «Тесты. Геометрия 7 – 9»
Л.М. Буланова, Ю.П. Дудницын «Проверочные задания по геометрии»