многогранники
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Конспект урока геометрии Правильные многогранники
Содержание
- 1. Конспект урока геометрии Правильные многогранники
- 2. Правильные многогранники. (Платоновы тела) Выпуклый многогранник
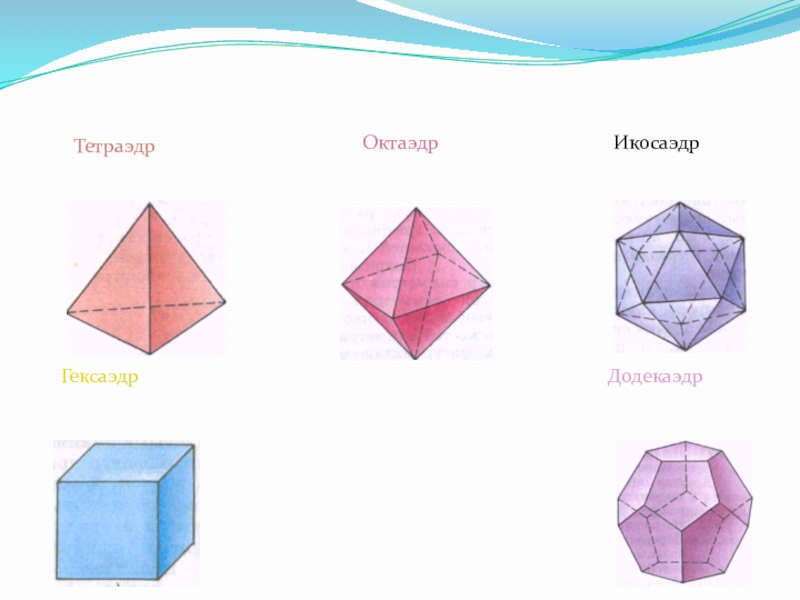
- 3. ДодекаэдрТетраэдр Октаэдр ИкосаэдрГексаэдр
- 4. Согласно философии Платона
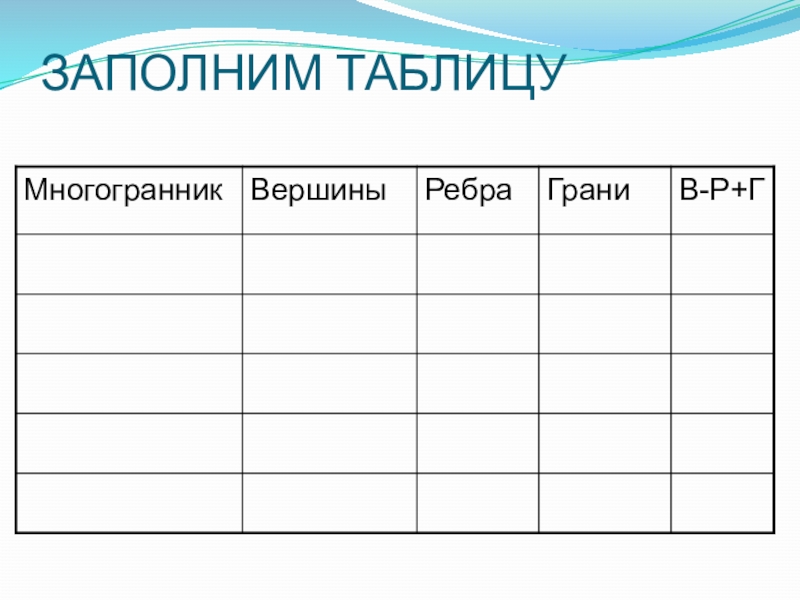
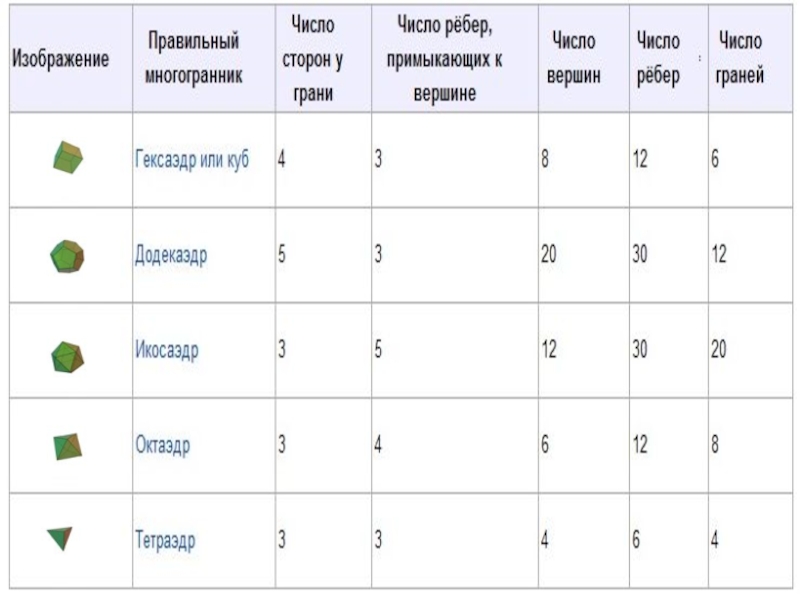
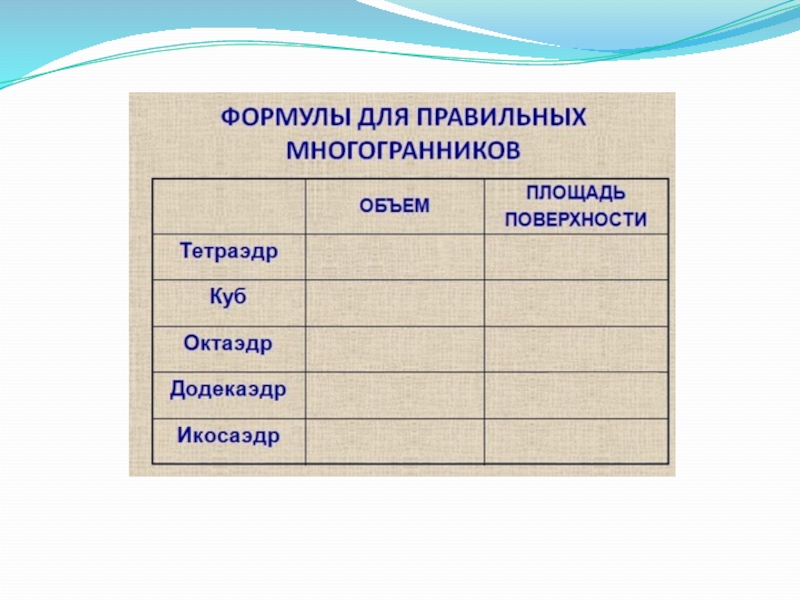
- 5. ЗАПОЛНИМ ТАБЛИЦУ
- 6. ТЕТРАЭДР «Тетраэдр» дословно: «четырехгранник.»
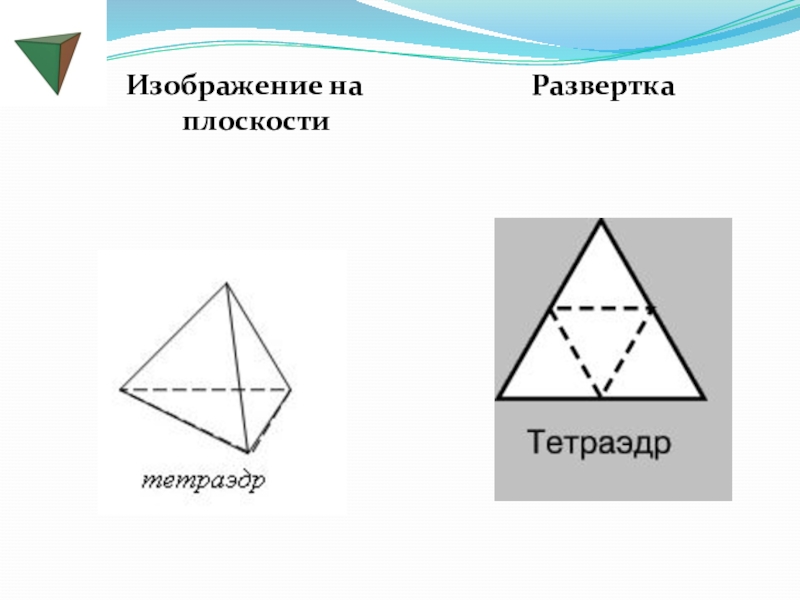
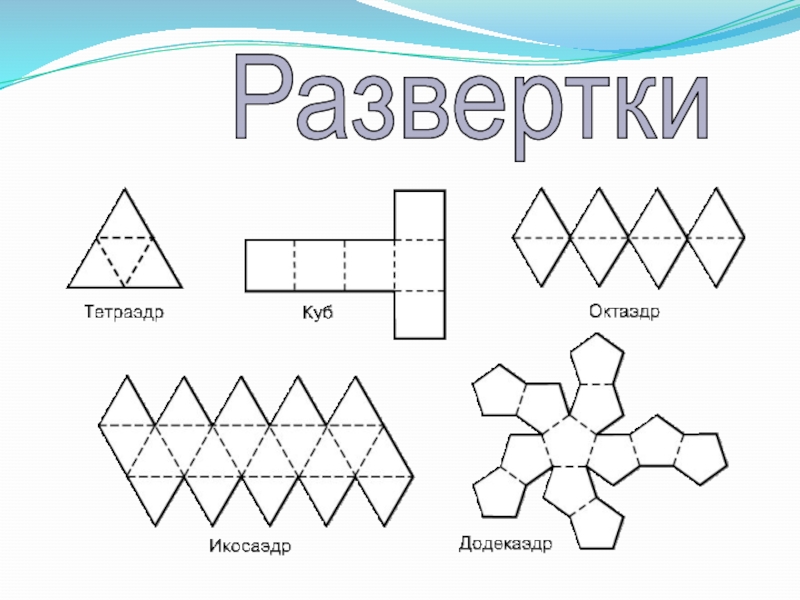
- 7. Изображение на плоскостиРазвертка
- 8. ГЕКСАЭДР(КУБ) «Гексаэдр» греч:«шестигранник».
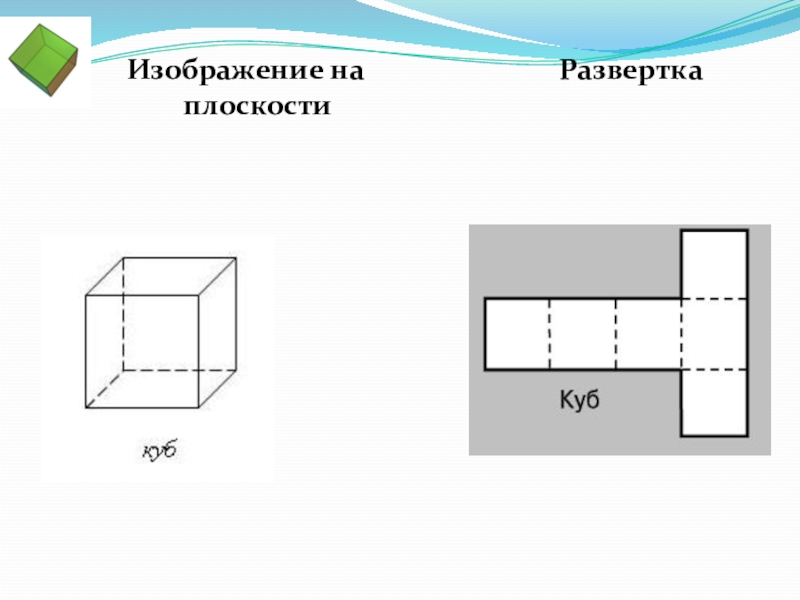
- 9. Изображение на плоскости Развертка
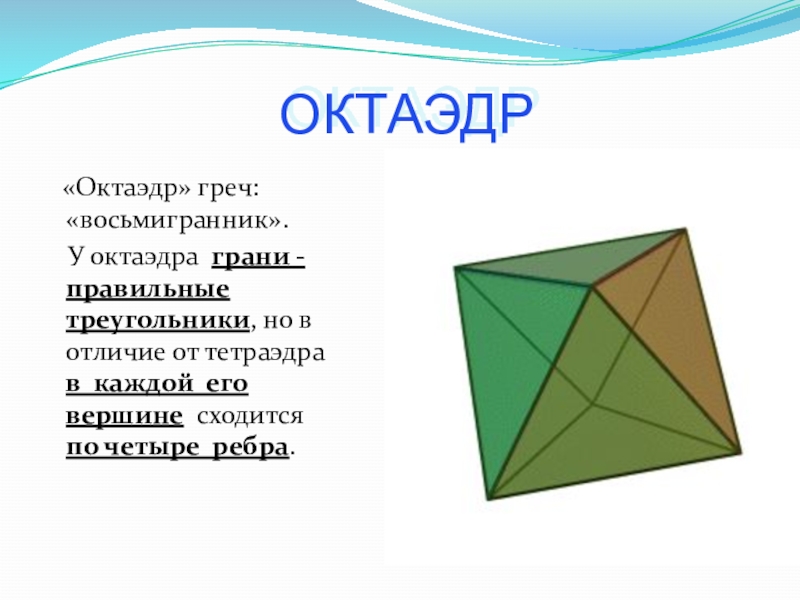
- 10. ОКТАЭДР «Октаэдр» греч: «восьмигранник». У
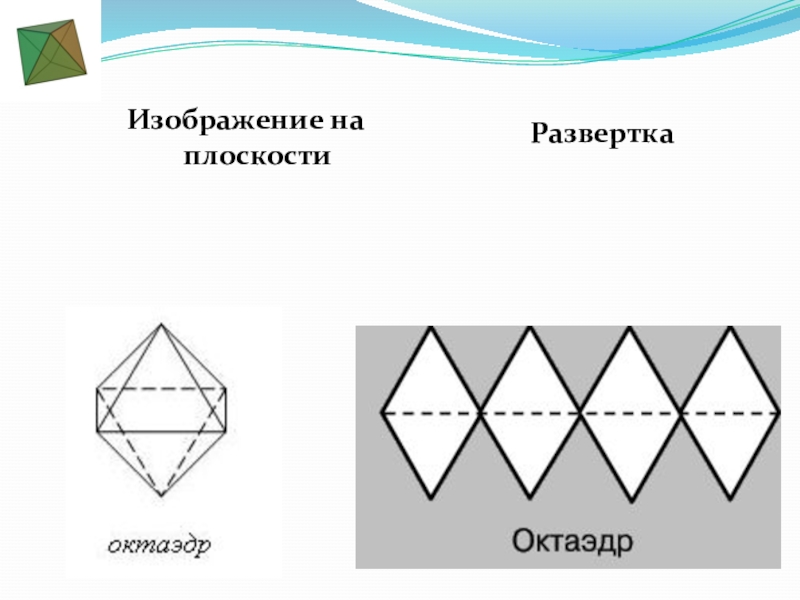
- 11. Изображение на плоскостиРазвертка
- 12. ДОДЕКАЭДР «Додекаэдр» греч: «двенадцатигранник». У додекаэдра
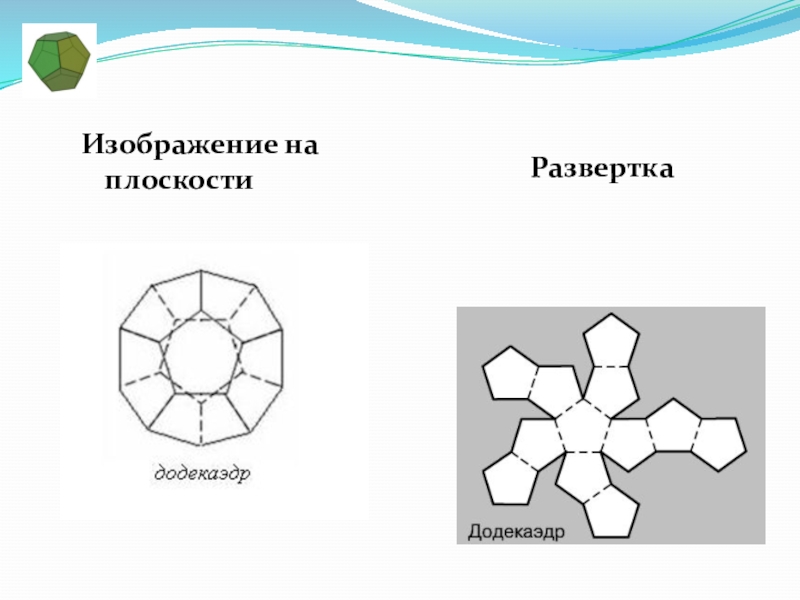
- 13. Изображение на плоскостиРазвертка
- 14. ИКОСАЭДР «Икосаэдр» греч: «двадцатигранник». У икосаэдра грани
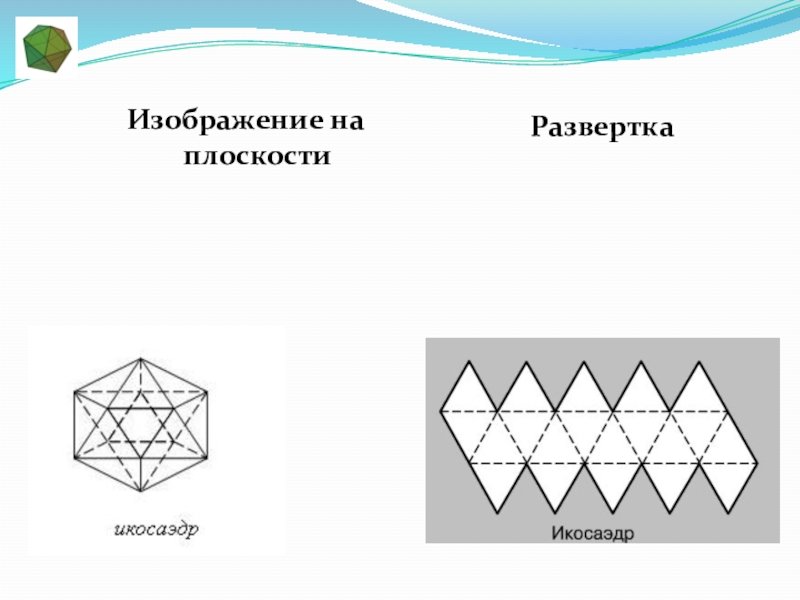
- 15. Изображение на плоскости Развертка
- 16. Большой интерес к формам
- 17. Сальвадор Дали на картине «Тайная вечеря»
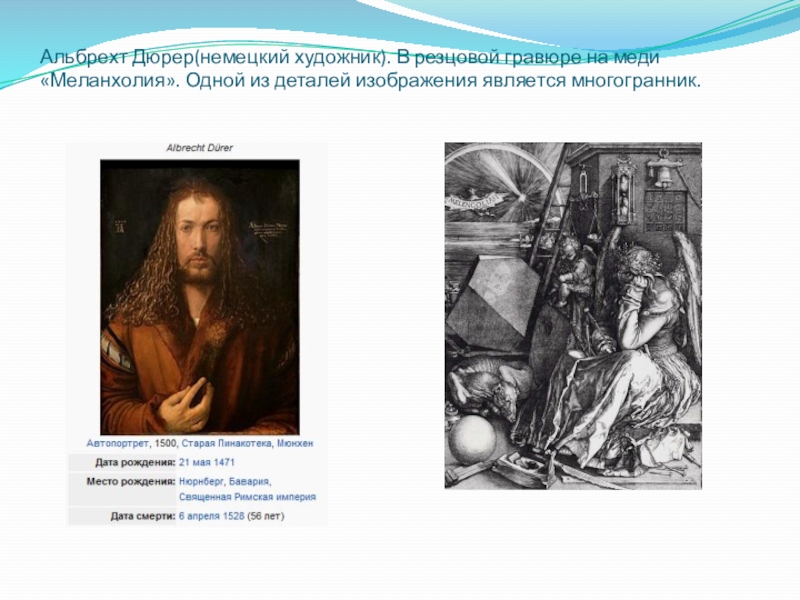
- 18. Альбрехт Дюрер(немецкий художник). В резцовой гравюре на меди «Меланхолия». Одной из деталей изображения является многогранник.
- 19. Еги́петские пирами́ды — величайшие
- 20. Вися́чие сады́ Семирами́ды
- 21. Учёным достаточно хорошо изучены правильные
- 22. Многогранники в природе Правильные многогранники
- 23. Многогранники в природе При производстве алюминия
- 24. Многогранники в природе Правильные многогранники встречаются так
- 25. Слайд 25
- 26. Архимедовыми телами называются полуправильные выпуклые многогранники, то
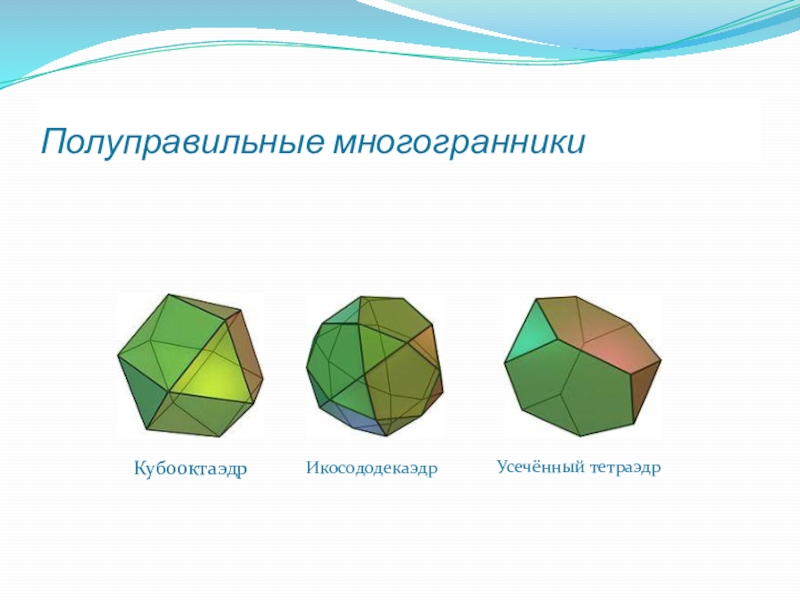
- 27. Полуправильные многогранникиКубооктаэдрИкосододекаэдрУсечённый тетраэдр
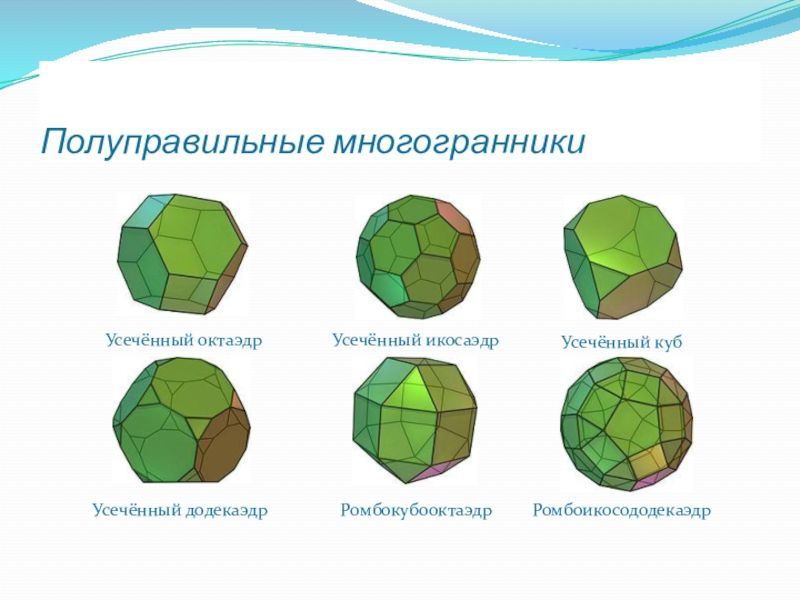
- 28. Полуправильные многогранникиУсечённый октаэдрУсечённый икосаэдрУсечённый кубУсечённый додекаэдрРомбокубооктаэдрРомбоикосододекаэдр
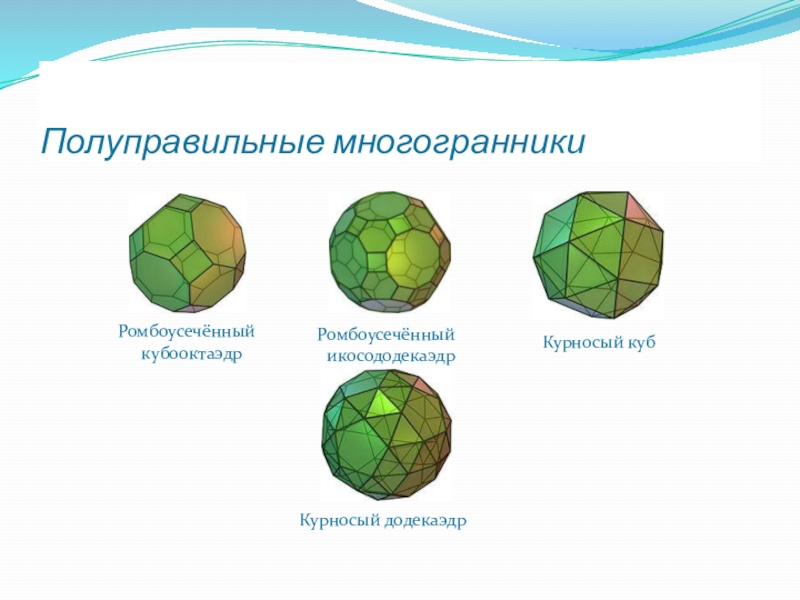
- 29. Полуправильные многогранникиРомбоусечённый кубооктаэдрРомбоусечённый икосододекаэдрКурносый кубКурносый додекаэдр
- 30. Звездчатые многогранникиЗвёздчатый многогранник (звёздчатое тело) — это
- 31. Звездчатые многогранникиДодекаэдр имеет 3 звёздчатые формы: малый звёздчатый додекаэдр, большой додекаэдр, большой звёздчатый додекаэдр
- 32. Звездчатые многогранникиИкосаэдр имеет 59 звёздчатых форм
- 33. Звездчатые многогранникиИкосододекаэдр имеет множество звёздчатых форм, первая из которых есть соединение икосаэдра и додекаэдра
- 34. Развертки
- 35. Слайд 35
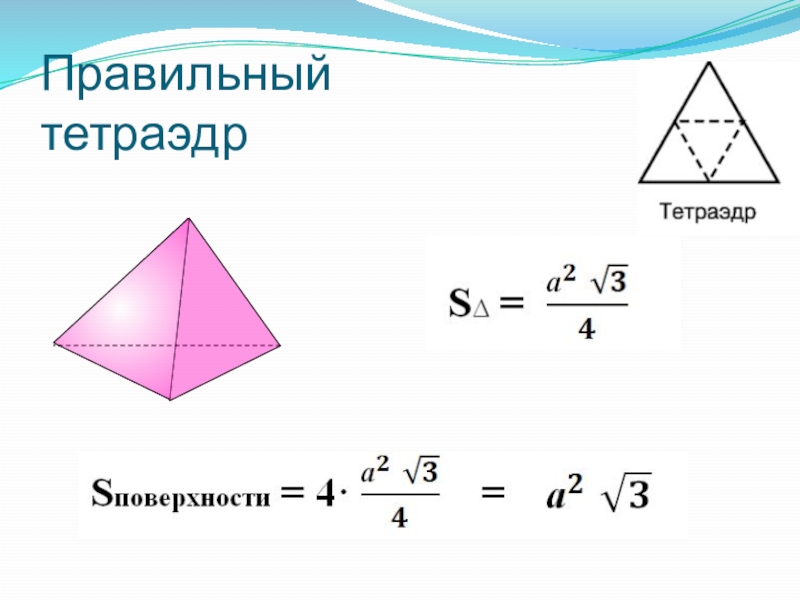
- 36. Правильный тетраэдр
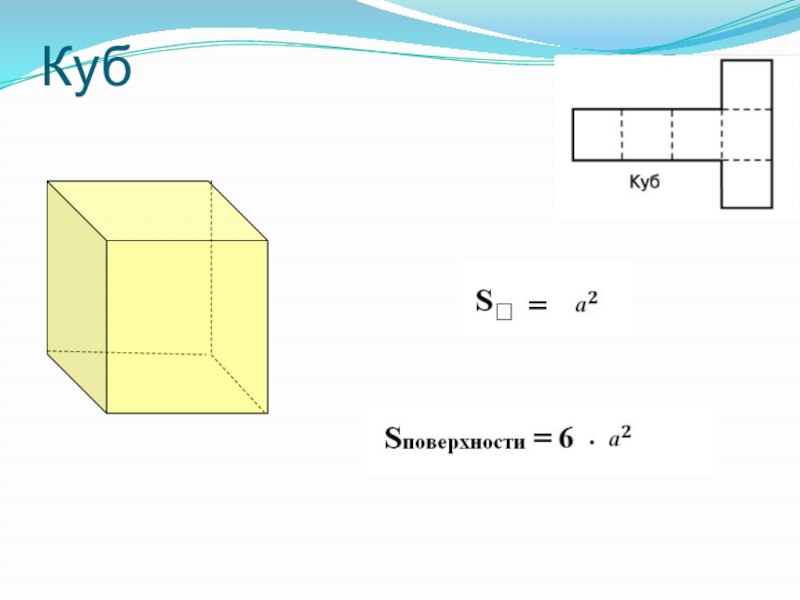
- 37. Куб
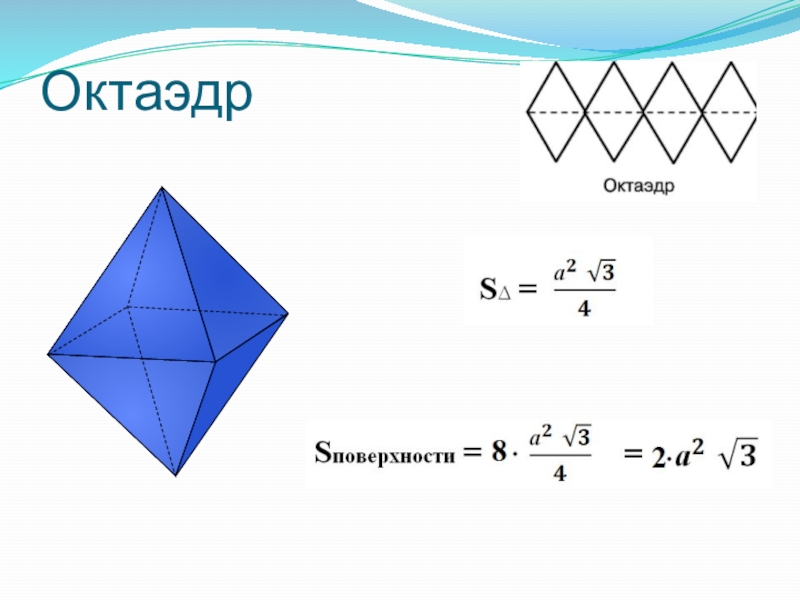
- 38. Октаэдр
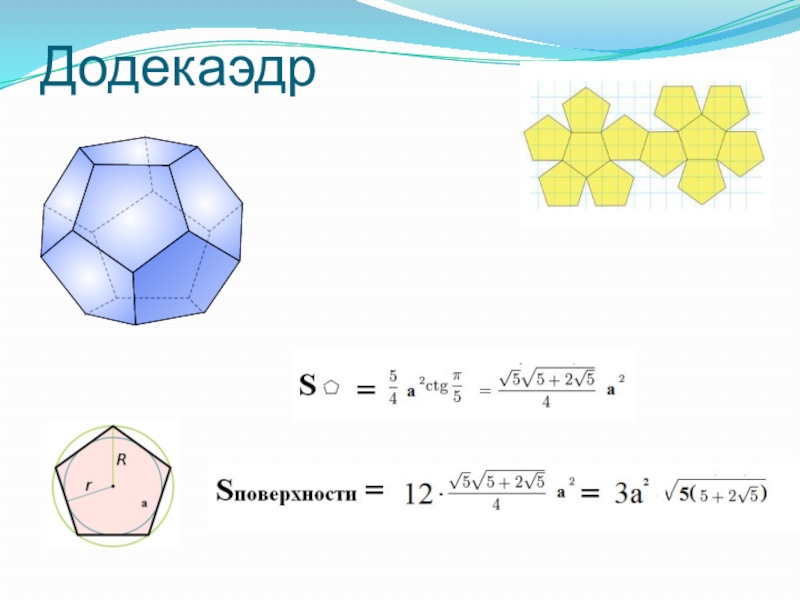
- 39. Додекаэдр
- 40. Икосаэдр
- 41. Слайд 41
- 42. СХОДСТВО и РАЗЛИЧИЕ 1. ПРАВИЛЬНЫЙ ТЕТРАЭДР- ПРАВИЛЬНАЯ ТРЕУГОЛЬНАЯ ПИРАМИДА.2. КУБ - ПРАВИЛЬНАЯ ЧЕТЫРЕХУГОЛЬНАЯ ПРИЗМА
Правильные многогранники. (Платоновы тела) Выпуклый многогранник называется правильным, если все его грани равные правильные многоугольники и в каждой вершине сходится одно и тоже число ребер.Существует пять типов правильных многогранников:1.Правильный тетраэдр;2.Правильный гексаэдр;3.Правильный икосаэдр;4. Правильный октаэдр;5. Правильный
Слайд 1Учитель математики
МБОУ СОШ № 2 г.Гагарин Смоленской области
Никитина Е.А.
Высшая кв.категория
Правильные
Слайд 2Правильные многогранники.
(Платоновы тела)
Выпуклый многогранник называется правильным, если все его
грани равные правильные многоугольники и в каждой вершине сходится одно и тоже число ребер.
Существует пять типов правильных многогранников:
1.Правильный тетраэдр;
2.Правильный гексаэдр;
3.Правильный икосаэдр;
4. Правильный октаэдр;
5. Правильный додекаэдр.
Существует пять типов правильных многогранников:
1.Правильный тетраэдр;
2.Правильный гексаэдр;
3.Правильный икосаэдр;
4. Правильный октаэдр;
5. Правильный додекаэдр.
Слайд 6ТЕТРАЭДР
«Тетраэдр» дословно: «четырехгранник.»
У тетраэдра
грани - правильные треугольники;
в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
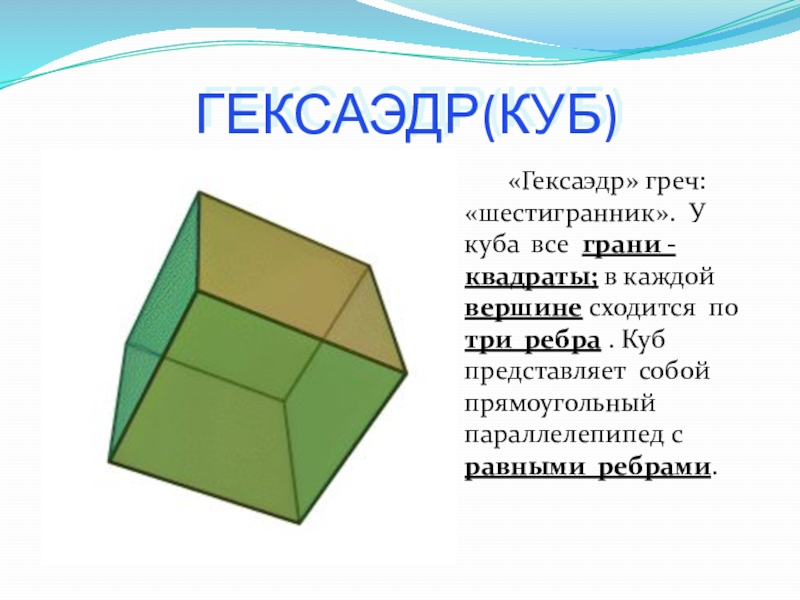
Слайд 8ГЕКСАЭДР(КУБ)
«Гексаэдр» греч:«шестигранник». У куба все грани
- квадраты; в каждой вершине сходится по три ребра . Куб представляет собой прямоугольный параллелепипед с равными ребрами.
Слайд 10ОКТАЭДР
«Октаэдр» греч: «восьмигранник».
У октаэдра грани - правильные
треугольники, но в отличие от тетраэдра в каждой его вершине сходится по четыре ребра.
Слайд 12ДОДЕКАЭДР
«Додекаэдр» греч: «двенадцатигранник». У додекаэдра грани - правильные пятиугольники.
В каждой вершине сходится по три ребра.
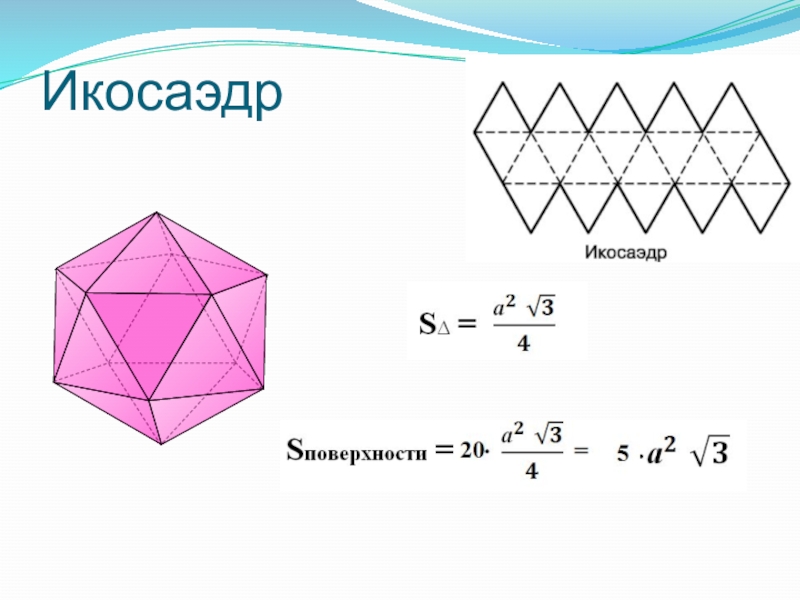
Слайд 14ИКОСАЭДР
«Икосаэдр» греч:
«двадцатигранник». У икосаэдра грани - правильные треугольники, но
в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер.
Слайд 16
Большой интерес к формам правильных многогранников проявляли также
скульпторы, архитекторы, художники. Их всех поражало совершенство, гармония многогранников. Леонардо да Винчи (1452 – 1519) увлекался теорией многогранников и часто изображал их на своих полотнах.
Слайд 17 Сальвадор Дали на картине «Тайная вечеря» изобразил И. Христа со
своими учениками на фоне огромного прозрачного додекаэдра.
Слайд 18Альбрехт Дюрер(немецкий художник). В резцовой гравюре на меди «Меланхолия». Одной из
деталей изображения является многогранник.
Слайд 19
Еги́петские пирами́ды — величайшие архитектурные памятники Древнего Египта,
среди которых одно из «семи чудес света» — пирамида Хеопса и почётный кандидат «новых семи чудес света» — Пирамиды Гизы. Пирамиды представляют собой огромные каменные сооружения пирамидальной формы, использовавшиеся в качестве гробниц для фараонов Древнего Египта.
Слайд 20
Вися́чие сады́ Семирами́ды — одно из Семи
чудес света. Более корректное название этого сооружения — Висячие сады Амитис (по другим источникам — Аманис): именно так звали жену вавилонского царя Навуходоносора II, ради которой сады были созданы. Предположительно располагались в древнем городе-государстве Вавилон, возле современного города Хилла.
Слайд 21
Учёным достаточно хорошо изучены правильные выпуклые многогранники, доказано,
что существует всего пять видов таких многогранников, но сам ли человек их придумал. Скорее всего – нет, он «подсмотрел» их у природы.
Слайд 22Многогранники в природе
Правильные многогранники – самые выгодные фигуры,
поэтому они широко распространены в природе. Подтверждением тому служит форма некоторых кристаллов. Например, кристаллы поваренной соли имеют форму куба. Правильный многогранник – икосаэдр передаёт форму кристаллов бора.
Слайд 23Многогранники в природе
При производстве алюминия пользуются алюминиево-калиевыми кварцами, монокристалл
которых имеет форму правильного октаэдра. Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана. Кристаллы этого химического вещества имеют форму додекаэдра. В разных химических реакциях применяется сурьменистый сернокислый натрий – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.
Слайд 24Многогранники в природе
Правильные многогранники встречаются так же и в живой
природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр.
Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Оно больше похоже на звёздчатый многогранник. Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление толщи воды.
Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр.
Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Оно больше похоже на звёздчатый многогранник. Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление толщи воды.
Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр.
Слайд 26Архимедовыми телами называются полуправильные выпуклые многогранники, то есть выпуклые многогранники, все
многогранные углы которых равны, а грани - правильные многоугольники нескольких типов.
Тела Архимеда
Слайд 28Полуправильные многогранники
Усечённый октаэдр
Усечённый икосаэдр
Усечённый куб
Усечённый додекаэдр
Ромбокубооктаэдр
Ромбоикосододекаэдр
Слайд 29Полуправильные многогранники
Ромбоусечённый
кубооктаэдр
Ромбоусечённый
икосододекаэдр
Курносый куб
Курносый додекаэдр
Слайд 30Звездчатые многогранники
Звёздчатый многогранник (звёздчатое тело) — это невыпуклый многогранник, грани которого
пересекаются между собой. Как и у незвёздчатых многогранников грани попарно соединяются в ребрах, при этом внутренние линии пересечения не считаются рёбрами.
Существует только одна звёздчатая форма октаэдра.
Существует только одна звёздчатая форма октаэдра.
Слайд 31Звездчатые многогранники
Додекаэдр имеет 3 звёздчатые формы: малый звёздчатый додекаэдр, большой додекаэдр,
большой звёздчатый додекаэдр
Слайд 33Звездчатые многогранники
Икосододекаэдр имеет множество звёздчатых форм, первая из которых есть соединение
икосаэдра и додекаэдра
Слайд 42СХОДСТВО и РАЗЛИЧИЕ
1. ПРАВИЛЬНЫЙ ТЕТРАЭДР- ПРАВИЛЬНАЯ ТРЕУГОЛЬНАЯ ПИРАМИДА.
2. КУБ -
ПРАВИЛЬНАЯ ЧЕТЫРЕХУГОЛЬНАЯ ПРИЗМА