«Человеку уже даны многие умения и дарования. Надо просто открыть эти дарования»
Б. Ничипоров
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Конкурсное задание Методический семинар на Республиканский конкурс Учитель математики 2015
Содержание
- 1. Конкурсное задание Методический семинар на Республиканский конкурс Учитель математики 2015
- 2. Одаренность – явление. Одаренные дети –
- 3. Система работы с одаренными детьми включает в себя
- 4. Технологии , которые я применяю на уроке:1.Личностно- ориентированное обучение;2.Проблемное обучение;3.Развивающее обучение;4. Компетентностный подход;
- 5. Личностно- ориентированное обучениедифференцированный подход к каждому ученику,
- 6. Проблемное обучение.1.Применяю сочетание традиционного объяснения с созданием
- 7. Развивающее обучение; это обучение, ориентированное на закономерности
- 8. Компетентностный подходРазвитие способностей ученика использовать усвоенные знания,
- 9. Одно из направлений моей работы- подготовка к олимпиадам.
- 10. Олимпиады-одна из наиболее эффективных и массовых форм
- 11. Цели проведения математических олимпиад:Расширение кругозора учащихся;Развитие интереса
- 12. Как я готовлю учащихся к олимпиадам?Я считаю,
- 13. Как я готовлю учащихся к олимпиадам?В свои
- 14. Качества, которые необходимо развить в ребенке, для
- 15. Успешное выступление на олимпиаде предполагает: а) психологическую
- 16. Рекомендую учащимся:читать дополнительную литературу по теории, вести
- 17. Часто повторяю своим ученикам слова Джорджа Полиа
- 18. В течении учебного года провожу олимпиады
- 19. Рекомендации участнику олимпиады:Внимательно изучи текст предложенных задач.Приступай
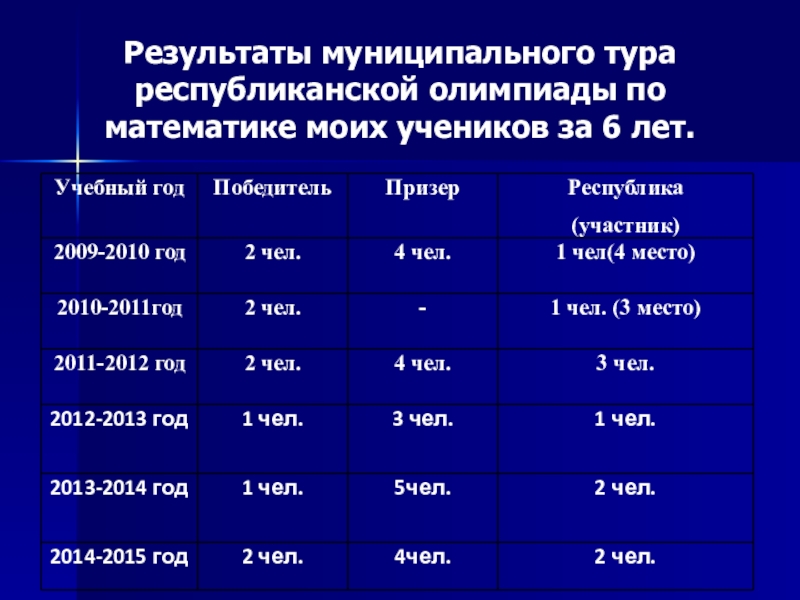
- 20. Результаты муниципального тура республиканской олимпиады по математике моих учеников за 6 лет.
Слайд 1Из опыта с одаренными детьми ( подготовка к олимпиадам) Шулаева Е.Н., учитель математики
Слайд 2Одаренность – явление.
Одаренные дети – проблема?
Одаренность - открытие в себе
Талант – дар легко, быстро и ярко выражать то, что проносится через внутренний мир человека.
(И.А.Ильин)
Слайд 3Система работы с одаренными детьми включает в себя следующие компоненты:
выявление одаренных
изучение индивидуальных способностей и возможностей одаренного ребёнка;
изучение интересов обучающихся в изучаемом предмете, разработка индивидуального образовательного маршрута для каждого одарённого ребёнка;
развитие творческих способностей на уроках;
развитие способностей во внеурочной деятельности (олимпиады, конкурсы, исследовательская и проектная работа);
создание условий для всестороннего развития одаренных детей.
формирование банка данных одарённых детей школы.
Слайд 4Технологии , которые я применяю на уроке:
1.Личностно- ориентированное обучение;
2.Проблемное обучение;
3.Развивающее обучение;
4.
Слайд 5Личностно- ориентированное обучение
дифференцированный подход к каждому ученику, возможность одаренным детям проявить
поиск лучших качеств личности, умение видеть в каждом ученике уникальную личность, уважать ее, понимать, принимать, верить в нее ("Все дети талантливы" - таково должно быть убеждение учителя);
создание для ребенка ситуации успеха, одобрения, поддержки, доброжелательности, чтобы школьная жизнедеятельность, учеба приносили ребенку радость);
исключение прямого принуждения, учитель не должен ставить акценты на отставание и на другие недостатки ребенка, необходимо понять причины детского незнания и неправильного поведения и устранять их, не унижая ребенка, не нанося ущерба его достоинству ("Ребенок хорош, плох его поступок");
предоставление возможности и помощи детям в реализации себя в положительной деятельности ("В каждом ребенке - чудо, помоги ему проявиться").
Слайд 6Проблемное обучение.
1.Применяю сочетание традиционного объяснения с созданием проблемных ситуаций, включая учащихся
2.Целенаправленно организую систему проблемных ситуаций при объяснении нового материала, решении задач, в результате чего усвоение знаний происходит в процессе самостоятельной поисковой деятельности. Все принимает характер открытия: надо самим искать и находить нужную теорему; осмысливать определения , аксиомы, правила.
3. Такая учебная деятельность в итоге приводит к изменению в структуре мыслительной деятельности, спецификой которой становится решение учебной проблемы путем рассуждения, выдвижения гипотезы, догадки или же сочетанием аналитического и эвристического путей развития.
Слайд 7Развивающее обучение;
это обучение, ориентированное на закономерности развития личности, в котором развивающий
Ведущие идеи: развивать самостоятельность мышления, способность к самообразованию и саморазвитию.
Слайд 8Компетентностный подход
Развитие способностей ученика использовать усвоенные знания, учебные умения и навыки,
способность структурировать данные (ситуацию), вычленять математические отношения, создавать математическую модель ситуации, анализировать и преобразовывать ее, интерпретировать полученные результаты.
Математическая компетенция учащегося способствует адекватному применению математики для решения возникающих в повседневной жизни проблем.
Слайд 10Олимпиады-
одна из наиболее эффективных и массовых форм внеклассной работы с учащимися.
не
это школа мышления и хороший учитель должен помочь ученику развить вкус к самостоятельным логическим рассуждениям.
Слайд 11Цели проведения математических олимпиад:
Расширение кругозора учащихся;
Развитие интереса учащихся к изучению математики;
Повышение
Выявление учащихся , способных к математике, для организации индивидуальной работы с ними.
Слайд 12Как я готовлю учащихся к олимпиадам?
Я считаю, что глубоко неправы те
Например, при изучении темы» Объемы тел» можно предложить задачу:
« Найти объем пирамиды, у которой боковые ребра образуют между собой углы по 90 градусов, а сами ребра имеют длины соответственно 3,4,5 см.»
Слайд 13Как я готовлю учащихся к олимпиадам?
В свои уроки и в домашнее
Во время уроков и дополнительных занятий стараюсь предложить учащимся нестандартные подходы в решении различных типов задач, вызвать у них потребность в поиске нестандартных методов решения.
Провожу собеседование и предлагаю всем желающим заниматься решением задач во внеурочное время, во время проведения муниципальных туров олимпиад и не только.
Слайд 14Качества, которые необходимо развить в ребенке, для успеха в олимпиаде:
С одной
А с другой стороны так же, как человек, если он блестящий музыкант, он не может играть, если он не играет ежедневно гаммы, и у него нет соответствующей техники. То же самое и с олимпийцами. Если они медленно или некачественно, с ошибками выполняют простые задания, то, естественно, они не добьются успеха.
Слайд 15Успешное выступление на олимпиаде предполагает:
а) психологическую подготовку школьника к выполнению
б) математическую одарённость;
в) умение собраться, сконцентрироваться на выполнение нескольких заданий за определённый промежуток времени;
г) математическую грамотность участника, умение строго записать решение задачи;
д) успешное овладение школьником изучаемых разделов математики.
Слайд 16Рекомендую учащимся:
читать дополнительную литературу по теории, вести поиск задач, решать их
Особенно важно, чтобы ребята знали общую идею, лежащую в основе всех методов и способов решения задач: решая новую задачу, сведи её к одной или нескольким ранее решенным задачам.
можно конечно, прорешать задачи конкретной олимпиады, запомнить их, в надежде встретить знакомый тип задач. Но можно совсем по-другому: понять самую суть задачи, построить цепочку рассуждений, ведущих к ответу и тем самым тренировать свои логические способности.
Слайд 17Часто повторяю своим ученикам слова Джорджа Полиа : «Чтобы научиться решать
Принимая участие в комиссии по проверке олимпиадных работ, я систематизирую и анализирую материалы олимпиад различного уровня, стараюсь объяснить решения заданий своим ученикам.
По текстам олимпиадных работ провожу олимпиады в классе, для тех кто хотел попасть на городскую олимпиаду, но не прошел на нее.
Слайд 18 В течении учебного года провожу олимпиады и матем.бои среди учащихся
Уделяю внимание задачам динамического характера, когда одна задача берётся в качестве основной и составляются подзадачи типа: подбери новые вопросы к условию, составь более общую задачу, сформулируй вопросы, которые раскрывают частные случаи и т.д
Стараемся принимать участие в течение года во всех олимпиадах, конкурсах, про которые появляется информация, понимая, что нельзя зацикливаться на городском уровне, надо расти дальше.
Слайд 19Рекомендации участнику олимпиады:
Внимательно изучи текст предложенных задач.
Приступай к решению той задачи,
Помни: на олимпиаде «лёгких» задач не бывает. Ищи «изюминку»!
Если задача вызывает трудности, попробуй упростить её условие, посмотреть частные или предельные случаи.
Решили задачу- сразу оформляйте её решение. Это поможет вам проверить логику и освободить мысли для других задач.
Если задача не получается, оставьте её на время и переходите к другой.
Задача становится проще, если её окружить родственными задачами.
ЕСЛИ ВАС НЕ НАГРАДИЛИ, ТО НИ В КОЕЙ МЕРЕ НЕ СЧИТАЙТЕ СЕБЯ «ПОБЕЖДЕННЫМИ»,- ОЛИМПИАДА НЕ ЗНАЕТ ТАКОГО ТЕРМИНА!