- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Комбинаторика на ЕГЭ
Содержание
- 1. Комбинаторика на ЕГЭ
- 2. КОМБИНАТОРИКАНА ЕГЭ
- 3. Слайд 3
- 4. Слайд 4
- 5. КОМБИНАТОРИКАНепосредственные подсчетыПравило умноженияПравило сложенияПерестановкиРазмещенияСочетания
- 6. НЕПОСРЕДСТВЕННЫЕ ПОДСЧЕТЫЛогический переборТаблица вариантовПолный графГраф-дерево
- 7. В случайном эксперименте симметричную монету бросают:а)дважды; б)трижды.Определите
- 8. В случайном эксперименте симметричную монету бросают:а)дважды; б)трижды.Определите
- 9. Таблица вариантов Сколько четных двузначных чисел можно составить из цифр 0, 1,2, 5, 8, 9?Ответ: 15.Решение.
- 10. Полный граф Андрей, Борис, Виктор и Григорий
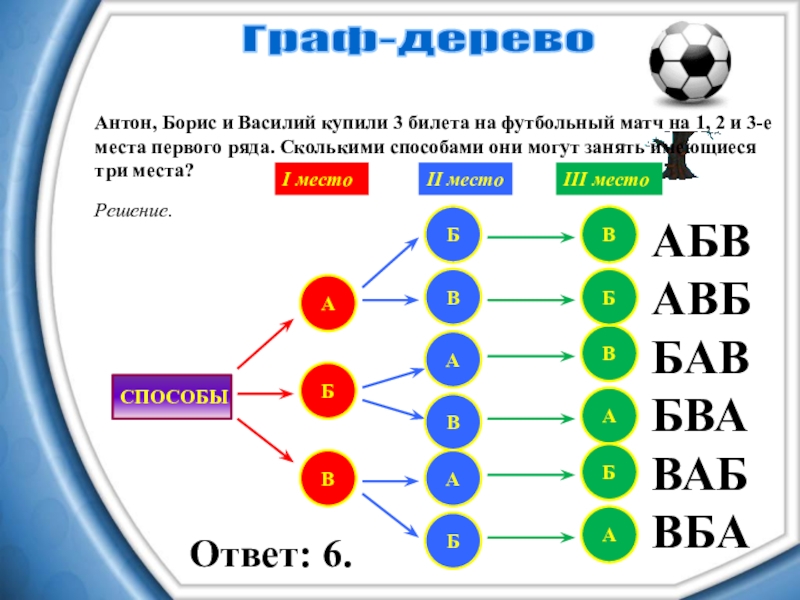
- 11. Антон, Борис и Василий купили 3 билета
- 12. ПРАВИЛО УМНОЖЕНИЯЕсли элемент множества А может быть
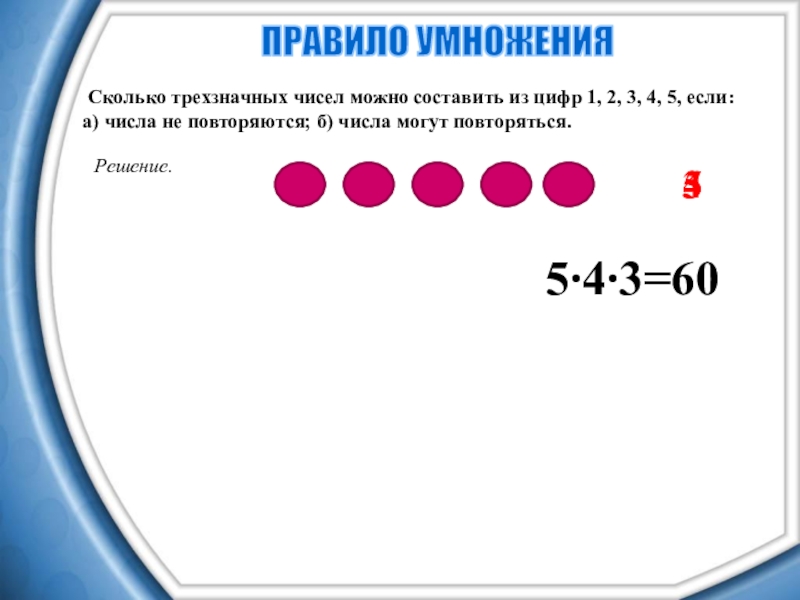
- 13. Сколько трехзначных чисел можно составить из
- 14. Сколько трехзначных чисел можно составить из
- 15. ПРАВИЛО СЛОЖЕНИЯЕсли элемент множества A можно выбрать
- 16. На блюдце лежит 8 яблок и 6
- 17. Пусть имеется n различных объектов. Будем переставлять их всеми
- 18. ПЕРЕСТАНОВКИСколько перестановок можно получить из букв, составляющих
- 19. Пусть имеется n различных объектов. Будем выбирать из них m объектов
- 20. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?РАЗМЕЩЕНИЯРешение.Ответ: 30.
- 21. Пусть имеется n различных объектов. Будем выбирать из них m объектов
- 22. Сколькими способами читатель может выбрать две книжки из пяти имеющихся?СОЧЕТАНИЯРешение.Ответ: 10.
- 23. ПОРЯДОК ВАЖЕН?ОПРЕДЕЛИТЕ n (общее количество объектов) И
- 24. ОПРЕДЕЛИТЕ n (общее количество объектов) И m
- 25. ОПРЕДЕЛИТЕ n (общее количество объектов) И m
- 26. ПОРЯДОК ВАЖЕН?НЕТПОВТОРЕНИЯ ЕСТЬ?НУЖНО ВЫБРАТЬ ВСЕ n ЭЛЕМЕНТОВ?ДАДАПОВТОРЕНИЯ
- 27. ПОРЯДОК ВАЖЕН?НЕТПОВТОРЕНИЯ ЕСТЬ?НЕТНУЖНО ВЫБРАТЬ ВСЕ n ЭЛЕМЕНТОВ?ПОВТОРЕНИЯ
- 28. ОПРЕДЕЛИТЕ n (общее количество объектов) И m
- 29. ОПРЕДЕЛИТЕ n (общее количество объектов) И m
- 30. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 5КОМБИНАТОРИКА
Непосредственные подсчеты
Правило умножения
Правило сложения
Перестановки
Размещения
Сочетания
Слайд 7В случайном эксперименте симметричную монету бросают:
а)дважды; б)трижды.
Определите все возможные комбинации выпадения
ОО
ОР
РО
РР
Решение.
Ответ: 4
Логический перебор
Слайд 8
В случайном эксперименте
симметричную
монету бросают:
а)дважды; б)трижды.
Определите все возможные
комбинации
выпадения
ООО
ООР
ОРО
ОРР
РОО
РОР
РРО
РРР
Решение.
Ответ: 8
Логический перебор
Слайд 9Таблица вариантов
Сколько четных двузначных чисел можно составить из цифр 0,
Ответ: 15.
Решение.
Слайд 10Полный граф
Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый
Ответ: 6.
Решение.
Слайд 11Антон, Борис и Василий купили 3 билета на футбольный матч на
Граф-дерево
Решение.
СПОСОБЫ
А
Б
В
Б
В
А
В
А
Б
В
В
Б
Ответ: 6.
А
Б
А
I место
II место
III место
АБВ
АВБ
БАВ
БВА
ВАБ
ВБА
Слайд 12ПРАВИЛО УМНОЖЕНИЯ
Если элемент множества А может быть выбран m способами, а
N= m ∙ n
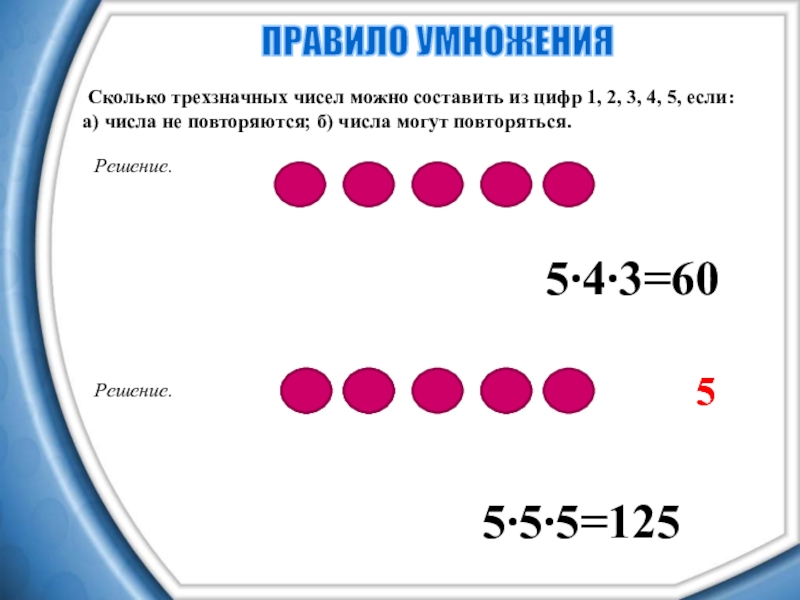
Слайд 13 Сколько трехзначных чисел можно составить из цифр 1, 2, 3,
а) числа не повторяются; б) числа могут повторяться.
ПРАВИЛО УМНОЖЕНИЯ
Решение.
5
4
3
5∙4∙3=60
Слайд 14 Сколько трехзначных чисел можно составить из цифр 1, 2, 3,
а) числа не повторяются; б) числа могут повторяться.
ПРАВИЛО УМНОЖЕНИЯ
Решение.
5
5∙5∙5=125
5
5
Решение.
5∙4∙3=60
Слайд 15ПРАВИЛО СЛОЖЕНИЯ
Если элемент множества A можно выбрать m способами, элемент множества
N=m+n
Слайд 16На блюдце лежит 8 яблок и 6 груш. Сколькими способами можно
ПРАВИЛО СЛОЖЕНИЯ
Решение.
m=8
n=6
N=8+6=14
Ответ: 14.
Слайд 17Пусть имеется n различных объектов. Будем переставлять их всеми возможными способами (число объектов остается
а их число равно
ПЕРЕСТАНОВКИ
Pn=n!
ПЕРЕСТАНОВКИ С ПОВТОРЕНИЯМИ
Слайд 18ПЕРЕСТАНОВКИ
Сколько перестановок можно получить из букв, составляющих слово «апельсин»?
Решение.
P8 = 8!
Ответ: 40320.
СПАНИЕЛЬ
Слайд 19Пусть имеется n различных объектов. Будем выбирать из них m объектов и переставлять всеми возможными способами
РАЗМЕЩЕНИЯ
РАЗМЕЩЕНИЯ С ПОВТОРЕНИЯМИ
Слайд 20Сколько можно составить сигналов из 6 флажков различного цвета, взятых по
РАЗМЕЩЕНИЯ
Решение.
Ответ: 30.
Слайд 21Пусть имеется n различных объектов. Будем выбирать из них m объектов всевозможными способами (то есть меняется
СОЧЕТАНИЯ
СОЧЕТАНИЯ С ПОВТОРЕНИЯМИ
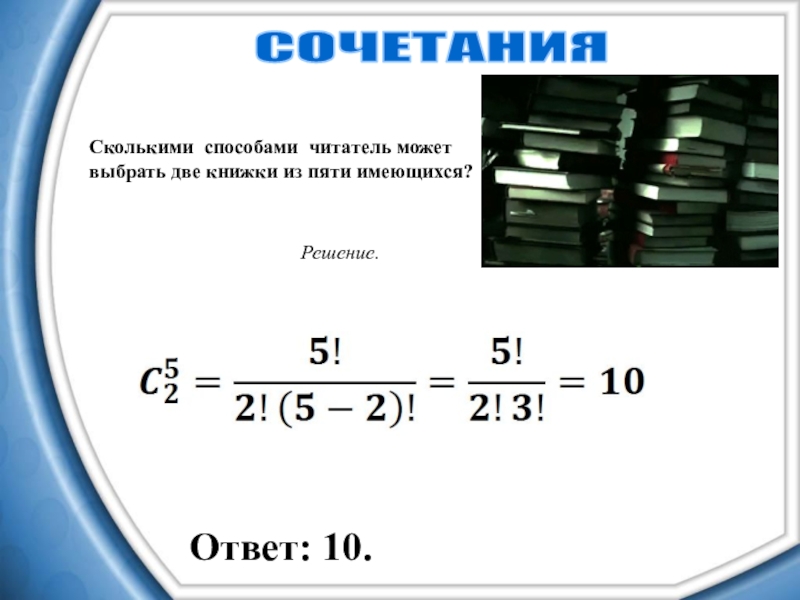
Слайд 22Сколькими способами читатель может выбрать две книжки из пяти имеющихся?
СОЧЕТАНИЯ
Решение.
Ответ: 10.
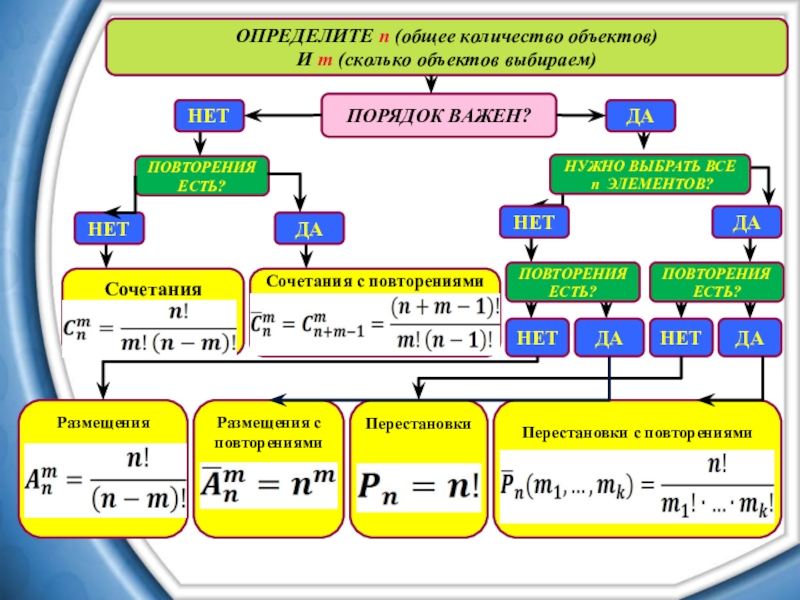
Слайд 23ПОРЯДОК ВАЖЕН?
ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем)
НЕТ
ДА
ПОВТОРЕНИЯ
НЕТ
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ДА
НЕТ
ДА
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
Сочетания
Сочетания с повторениями
НЕТ
ДА
НЕТ
ДА
Перестановки с повторениями
Перестановки
Размещения с повторениями
Размещения
Слайд 24ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем)
ПОРЯДОК ВАЖЕН?
НЕТ
ПОВТОРЕНИЯ
НЕТ
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ДА
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
Сочетания
Сочетания с повторениями
НЕТ
ДА
ДА
Перестановки с повторениями
Перестановки
Размещения с повторениями
Размещения
Pn=n!
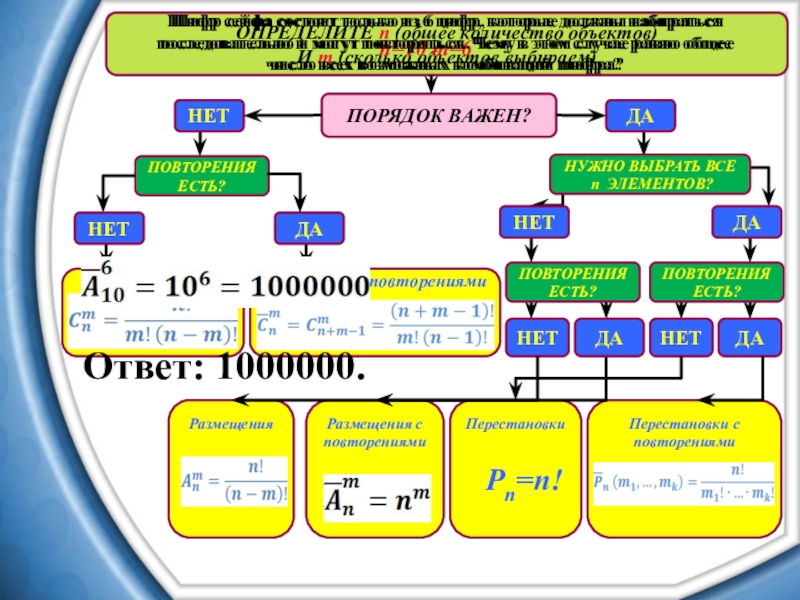
n=10 m=6
НЕТ
Ответ: 1000000.
Шифр сейфа состоит только из 6 цифр, которые должны набираться
последовательно и могут повторяться. Чему в этом случае равно общее число всех возможных комбинаций шифра?
Шифр сейфа состоит только из 6 цифр, которые должны набираться
последовательно и могут повторяться. Чему в этом случае равно общее
число всех возможных комбинаций шифра?
ДА
НЕТ
ДА
Слайд 25ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем)
ПОРЯДОК ВАЖЕН?
НЕТ
ДА
ПОВТОРЕНИЯ
НЕТ
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ДА
НЕТ
ДА
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
Сочетания
Сочетания с повторениями
НЕТ
ДА
ДА
Перестановки с повторениями
Перестановки
Размещения с повторениями
Размещения
Pn=n!
n=10 m=5
НЕТ
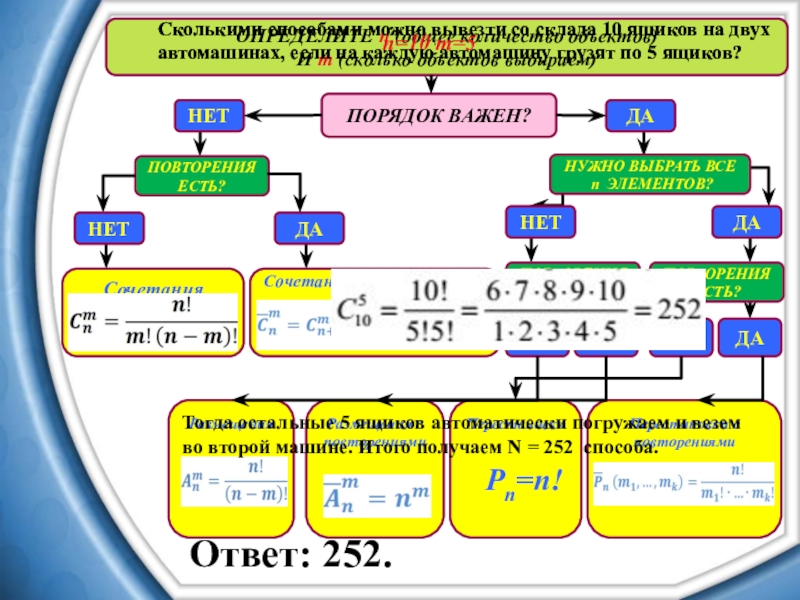
Тогда остальные 5 ящиков автоматически погружаем и везем во второй машине. Итого получаем N = 252 способа.
Ответ: 252.
Сколькими способами можно вывезти со склада 10 ящиков на двух автомашинах, если на каждую автомашину грузят по 5 ящиков?
Сколькими способами можно вывезти со склада 10 ящиков на двух автомашинах, если на каждую автомашину грузят по 5 ящиков?
Слайд 26ПОРЯДОК ВАЖЕН?
НЕТ
ПОВТОРЕНИЯ ЕСТЬ?
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ДА
ДА
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
Сочетания
Сочетания с повторениями
НЕТ
ДА
ДА
Перестановки
Перестановки
Размещения с повторениями
Размещения
Pn=n!
n=11 m=5
НЕТ
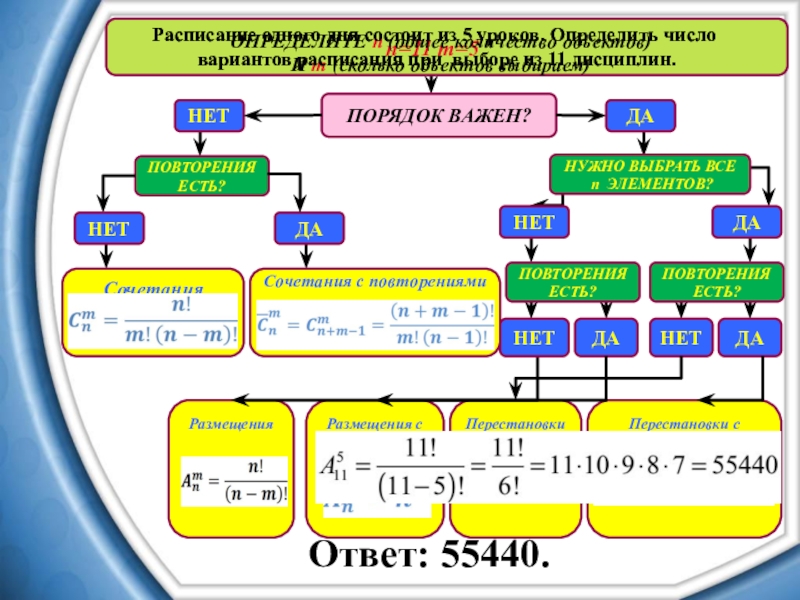
Ответ: 55440.
ДА
НЕТ
НЕТ
ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем)
Расписание одного дня состоит из 5 уроков. Определить число
вариантов расписания при выборе из 11 дисциплин.
Расписание одного дня состоит из 5 уроков. Определить число
вариантов расписания при выборе из 11 дисциплин.
Слайд 27ПОРЯДОК ВАЖЕН?
НЕТ
ПОВТОРЕНИЯ ЕСТЬ?
НЕТ
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
Сочетания
Сочетания с повторениями
ДА
ДА
Перестановки
Перестановки
Размещения с повторениями
Размещения
Pn=n!
n=4 m=4
НЕТ
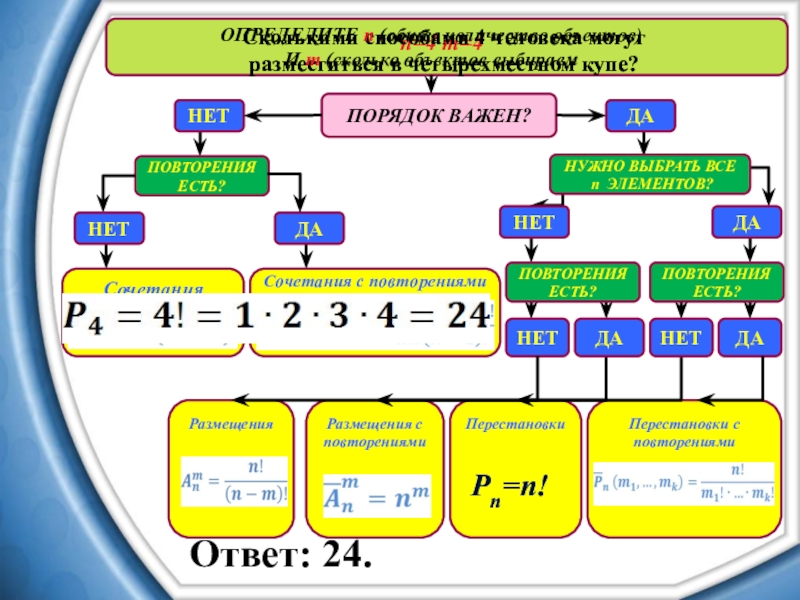
Ответ: 24.
Сколькими способами 4 человека могут разместиться в четырехместном купе?
НЕТ
ДА
Сколькими способами 4 человека могут разместиться в четырехместном купе?
ДА
ДА
НЕТ
ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем
Pn=n!
Слайд 28ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем)
ПОРЯДОК ВАЖЕН?
НЕТ
ДА
ПОВТОРЕНИЯ
НЕТ
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ДА
НЕТ
ДА
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
Сочетания
Сочетания с повторениями
НЕТ
ДА
Перестановки с повторениями
Перестановки
Размещения с повторениями
Размещения
Pn=n!
n=10 m=12
НЕТ
ДА
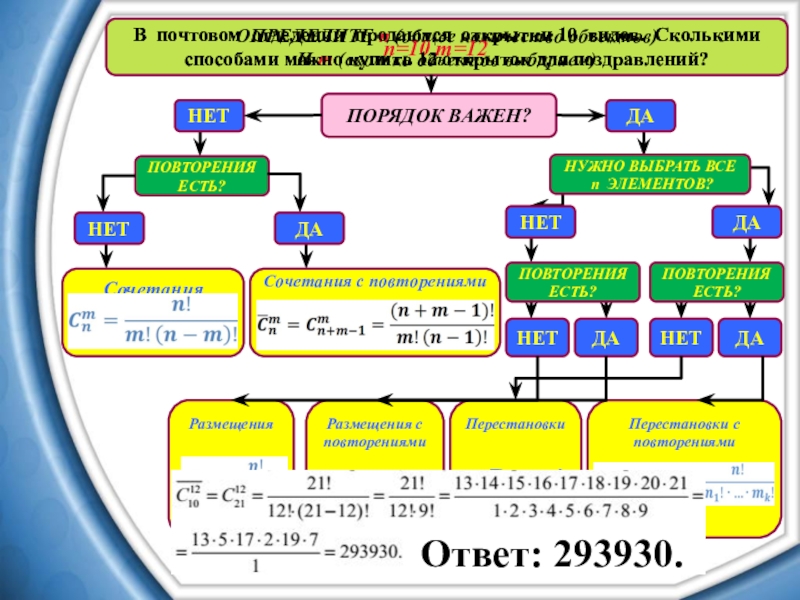
Ответ: 293930.
В почтовом отделении продаются открытки 10 видов. Сколькими
способами можно купить 12 открыток для поздравлений?
В почтовом отделении продаются открытки 10 видов. Сколькими
способами можно купить 12 открыток для поздравлений?
Слайд 29ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем)
ПОРЯДОК ВАЖЕН?
НЕТ
ПОВТОРЕНИЯ
НЕТ
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
Сочетания
Сочетания с повторениями
ДА
Перестановки с повторениями
Перестановки
Размещения с повторениями
Размещения
Pn=n!
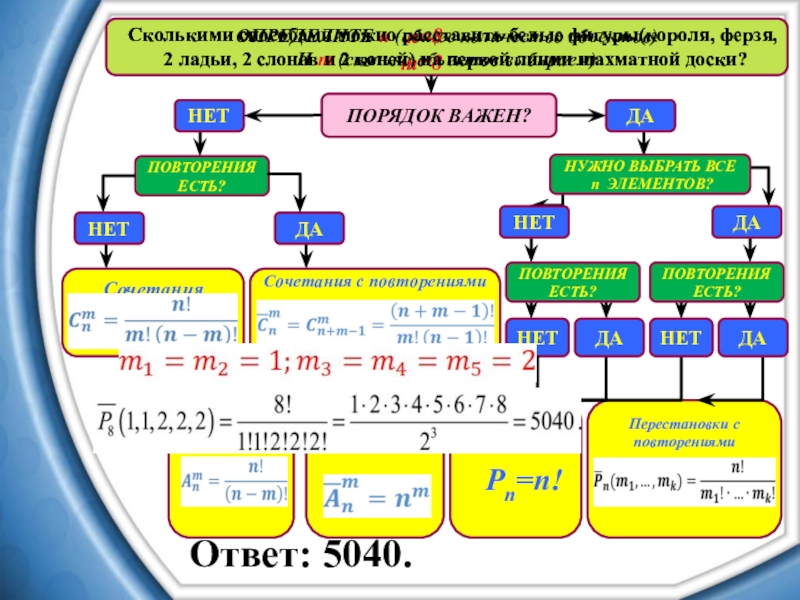
n=8
m=8
НЕТ
Ответ: 5040.
НЕТ
ДА
НЕТ
Сколькими способами можно расставить белые фигуры(короля, ферзя,
2 ладьи, 2 слонов и 2 коней) на первой линии шахматной доски?
Сколькими способами можно расставить белые фигуры(короля, ферзя,
2 ладьи, 2 слонов и 2 коней) на первой линии шахматной доски?
ДА
ДА
ДА