- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Ключевые задачи как фактор повышения эффективности обучения геометрии
Содержание
- 1. Ключевые задачи как фактор повышения эффективности обучения геометрии
- 2. Каждая решенная мною задача становилась образцом, который
- 3. В практической деятельности закрепляются теоретические знанияРазвивается подлинная
- 4. Математическая задача называется ключевой, если ее содержание либо метод ее решения используется при решении других задач
- 5. Применение ключевых задач позволяет учить методам решения математических задачоблегчает поиск решениядает возможность индивидуализировать процесс их решения
- 6. Метод ключевых задач обеспечиваетПонимание учащимися природы и
- 7. Перед отбором задач учителю необходимопроанализировать, какие умения
- 8. Методы отбора ключевых задач1)Аналитический, анализ любой задачи
- 9. Последовательность задач, разбираемых на урокеначинать лучше с
- 10. Контролю усвоения ключевых задач подлежитумение осуществлять самоконтроль
- 11. Специальные уроки
- 12. Ключевая задачаЗадача-фактЗадача -методЗадача - факт и методКлючевая задача – это отдельная методическая единица
- 13. Докажите, что в прямоугольном треугольнике медиана, проведенная
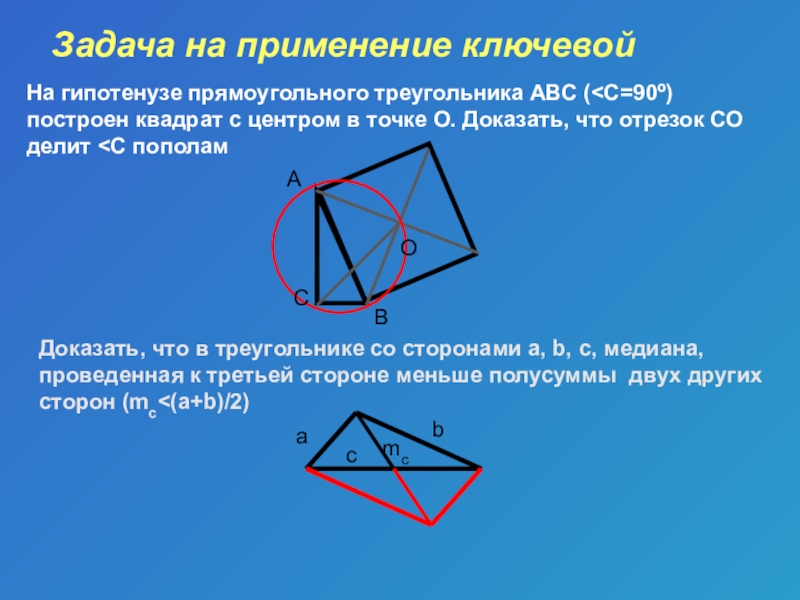
- 14. Задача на применение ключевойНа гипотенузе прямоугольного треугольника АВС (
- 15. Ключевая задача на тему «Свойства биссектрисы угла
- 16. Упражнения на распознавание ключевой задачи 1. В
- 17. «Обучение математике имеет смысл только тогда, когда
- 18. Спасибо за внимание
Слайд 2Каждая решенная мною задача становилась образцом, который служил впоследствии для решения
Р. Декарт
Слайд 3В практической деятельности закрепляются теоретические знания
Развивается подлинная творческая активность
Развивается мышление
Основная цель
При решении задач
Слайд 4Математическая задача называется ключевой, если ее содержание либо метод ее решения
Слайд 5
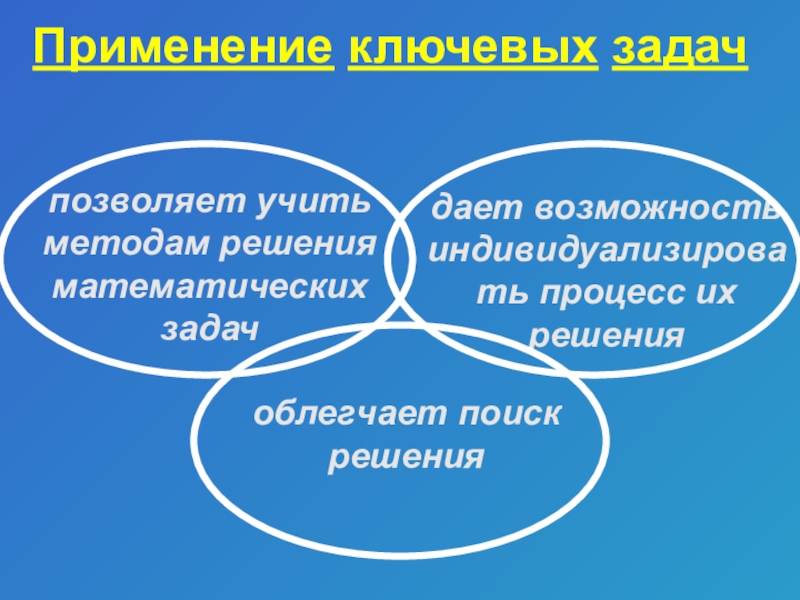
Применение ключевых задач
позволяет учить методам решения математических задач
облегчает поиск решения
дает
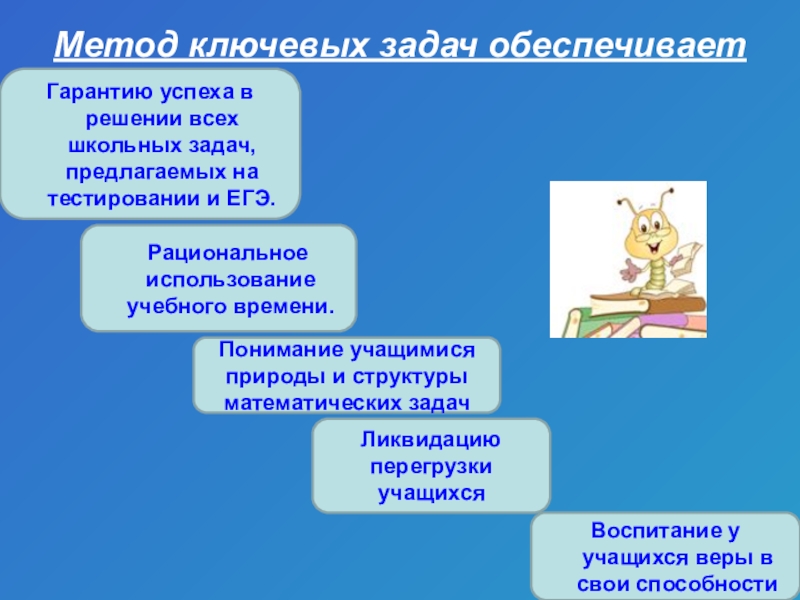
Слайд 6Метод ключевых задач обеспечивает
Понимание учащимися природы и структуры математических задач
Ликвидацию перегрузки
Гарантию успеха в решении всех школьных задач, предлагаемых на тестировании и ЕГЭ.
Рациональное использование учебного времени.
Воспитание у учащихся веры в свои способности
Слайд 7Перед отбором задач учителю необходимо
проанализировать, какие умения должны быть сформированы у
соотнести просматриваемые задачи по теме с планируемыми умениями;
выделить то минимальное их число, овладев решениями которых, школьник сможет решить любую задачу
Слайд 8
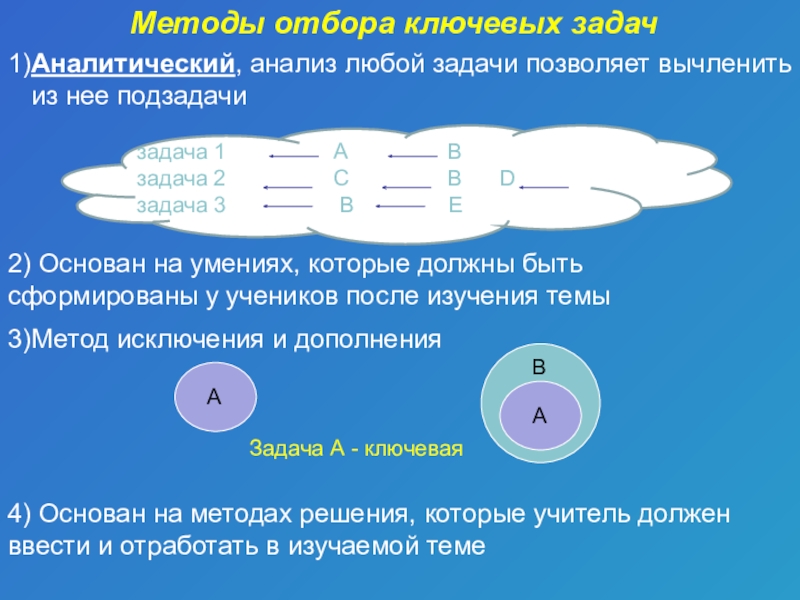
Методы отбора ключевых задач
1)Аналитический, анализ любой задачи позволяет вычленить из нее
задача 1 А В
задача 2 С В D
задача 3 B Е
3)Метод исключения и дополнения
2) Основан на умениях, которые должны быть сформированы у учеников после изучения темы
А
А
В
Задача А - ключевая
4) Основан на методах решения, которые учитель должен ввести и отработать в изучаемой теме
Слайд 9Последовательность задач, разбираемых на уроке
начинать лучше с самых простых ключевых задач;
задачи,
cамые яркие задачи лучше отнести на вторую часть урока;
желательно чередовать задачи с обширными записями и те, которые не предполагают громоздких обоснований;
задачи, связанные с предыдущей темой, лучше включать в число первых, а активно используемые в последующих темах - позднее
Слайд 10Контролю усвоения ключевых задач подлежит
умение осуществлять самоконтроль деятельности по решению ключевых
умение решать ключевые задачи
умение правильно оформлять решение ключевых задач
умение школьников распознавать ключевые задачи
умение запоминать такие задачи, иметь их в своем арсенале)
Слайд 12Ключевая задача
Задача-факт
Задача -метод
Задача - факт и метод
Ключевая задача – это отдельная
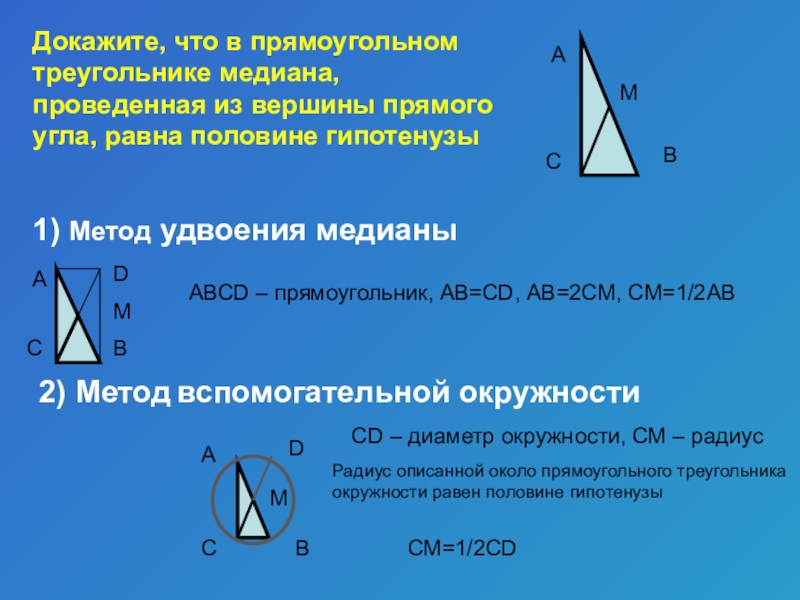
Слайд 13Докажите, что в прямоугольном треугольнике медиана, проведенная из вершины прямого угла,
А
С
В
1) Метод удвоения медианы
А
С
В
М
D
M
АВСD – прямоугольник, АВ=СD, АВ=2СМ, СМ=1/2АВ
2) Метод вспомогательной окружности
А
В
С
М
D
CD – диаметр окружности, СМ – радиус
Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы
СМ=1/2СD
Слайд 14Задача на применение ключевой
На гипотенузе прямоугольного треугольника АВС (
А
С
В
О
Доказать, что в треугольнике со сторонами а, b, c, медиана, проведенная к третьей стороне меньше полусуммы двух других сторон (mc<(a+b)/2)
а
b
c
mc
Слайд 15Ключевая задача на тему
«Свойства биссектрисы угла треугольника»
Ключевая задача: Биссектриса внутреннего
А
В
С
D
Задача на применение ключевой: Расстояние от вершины прямого угла до гипотенузы равно а, а до точки пересечения биссектрисы меньшего угла с меньшим катетом равно b. Найдите длину меньшего катета
Слайд 16Упражнения на распознавание ключевой задачи
1. В треугольнике АВС
2.В прямоугольный треугольник вписана полуокружность так, что диаметр лежит на гипотенузе, а центр делит гипотенузу на отрезки длиной 15 и 20. Найдите радиус полуокружности.
3.Точка на гипотенузе, равноудаленная от обоих катетов, делит гипотенузу на отрезки длиной 30 и 40. Найдите катеты треугольника
4. В прямоугольный треугольник с углом 60° вписан ромб со стороной, равной 6, так, что угол в 60° у них общий и все вершины ромба лежат на сторонах треугольника. Найдите стороны треугольника.
5. В равнобедренном треугольнике основание и боковая сторона равны соответственно 5 и 20. Найдите биссектрису угла при основании треугольника.