СОШ19» г.Энгельса
Руководители:
Шабашова Г.В, Безверхая О.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Исследовательская работа Мир простых чисел
Содержание
- 1. Исследовательская работа Мир простых чисел
- 2. «Математика есть царица наук, а арифметика есть
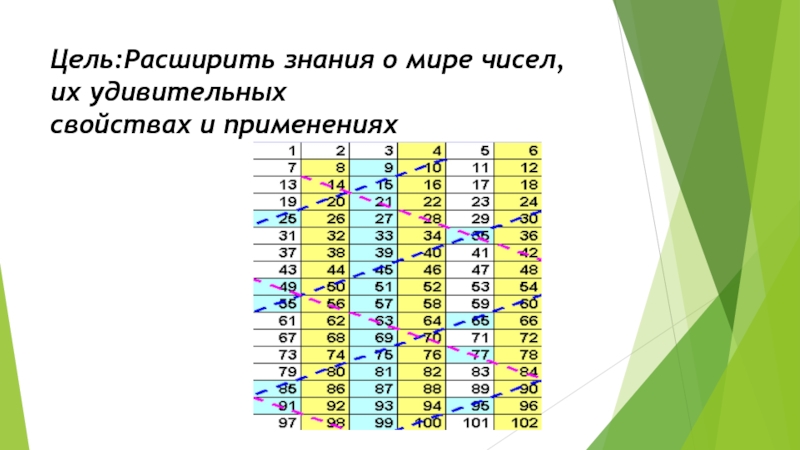
- 3. Цель:Расширить знания о мире чисел, их удивительных свойствах и применениях
- 4. Задачи:Знакомство с методом “отсеивания”простых чисел от составных – решетомЭратосфена.- Знакомство с совершеннымичислами, числами –близнецами.
- 5. Решето Эратосфена
- 6. По числу делителей все натуральные числа делятся
- 7. • Пифагор (6 век до н. э)
- 8. Простые числа-близнецы это пара простых чисел,отличающихся на
- 9. • Выводы: Мир чисел велик, но не
- 10. • Литература:• О. С. Шейнина, Г.М. Соловьева.Математика.
«Математика есть царица наук, а арифметика есть царица математики»Немецкий математик Карл Гаусс (1777 – 1855)В начальной школе, где учился мальчик КарлГаусс, ставший потом знаменитымматематиком, учитель, чтобы занять класс напродолжительное время самостоятельнойработой, дал детям задание – вычислить
Слайд 2«Математика есть царица наук,
а арифметика есть царица математики»
Немецкий математик Карл Гаусс
(1777 – 1855)
В начальной школе, где учился мальчик Карл
Гаусс, ставший потом знаменитым
математиком, учитель, чтобы занять класс на
продолжительное время самостоятельной
работой, дал детям задание – вычислить сумму
всех натуральных чисел от 1 до 100. Но
маленький Гаусс это задание выполнил почти
моментально: «Готово, 5050» Весь класс был
поражен, как быстро он решил задачу. Был
поражен и учитель. Когда учитель спросил
Карла, как он решил задачу, тот объяснил, что
каждая пара чисел, одинаково отстоящих от
концов указанного ряда, составляет в сумме
101,а так как таких пар 50, то нужно
умножить101 на 50,получится 5050.
В начальной школе, где учился мальчик Карл
Гаусс, ставший потом знаменитым
математиком, учитель, чтобы занять класс на
продолжительное время самостоятельной
работой, дал детям задание – вычислить сумму
всех натуральных чисел от 1 до 100. Но
маленький Гаусс это задание выполнил почти
моментально: «Готово, 5050» Весь класс был
поражен, как быстро он решил задачу. Был
поражен и учитель. Когда учитель спросил
Карла, как он решил задачу, тот объяснил, что
каждая пара чисел, одинаково отстоящих от
концов указанного ряда, составляет в сумме
101,а так как таких пар 50, то нужно
умножить101 на 50,получится 5050.
Слайд 4Задачи:
Знакомство с методом “отсеивания”
простых чисел от составных – решетом
Эратосфена.
- Знакомство с
совершенными
числами, числами –
близнецами.
числами, числами –
близнецами.
Слайд 6По числу делителей все натуральные числа делятся на 3 группы: 1-Единица (1) –
не считается простым числом;
2-Простые числа, имеющие только два делителя (один
и само число);
3-Составные числа, имеющие больше двух делителей;
Как установить, число простое или составное? Этот
вопрос волновал многих математиков. Первым начал
составлять таблицу простых чисел древнегреческий
математик Эратосфен, живший в 3 веке до н.э.
Слайд 7• Пифагор (6 век до н. э) и его ученики изучали
вопрос о делимости чисел. Число,
равное сумме всех его делителей (без самого числа), назывались
совершенным числом.
• Например:
• 6 (6 =1+ 2 +3),
• 28 (28 =1+ 2+ 4+ 7+ 14) - совершенные числа
• Пока известно только 27 совершенных чисел, до сих пор ученые не знают, есть
ли самое большое совершенное число
Слайд 8Простые числа-близнецы это пара простых чисел,
отличающихся на 2.
Все пары простых -
близнецов, кроме (3, 5)имеют вид
(6n+/-1)
Первые простые числа-близнецы:
(3,5),(5,7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61),
(71, 73), (101,103), (107, 109), (137, 139), (149, 151),
(179, 181), (191, 193), (197, 199), (227, 229), (239,
241), (269, 271), (281, 283), (311, 313), (347, 349),
(419, 421), (431, 433), (461, 463), (521, 523), (569,
571), (599, 601), (617, 619), (641, 643), (659, 661),
(809, 811), (821, 823), (827, 829), (857, 859), (881, 883)
Предполагается, что таких пар бесконечно много, но
это не доказано
(6n+/-1)
Первые простые числа-близнецы:
(3,5),(5,7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61),
(71, 73), (101,103), (107, 109), (137, 139), (149, 151),
(179, 181), (191, 193), (197, 199), (227, 229), (239,
241), (269, 271), (281, 283), (311, 313), (347, 349),
(419, 421), (431, 433), (461, 463), (521, 523), (569,
571), (599, 601), (617, 619), (641, 643), (659, 661),
(809, 811), (821, 823), (827, 829), (857, 859), (881, 883)
Предполагается, что таких пар бесконечно много, но
это не доказано
Слайд 9• Выводы:
Мир чисел велик, но не все еще в этом
мире изучено.
Может быть именно нам суждено открыть
следующее совершенное число или найти самую большую пару чисел –
близнецов.
Может быть именно нам суждено открыть
следующее совершенное число или найти самую большую пару чисел –
близнецов.
Слайд 10• Литература:
• О. С. Шейнина, Г.М. Соловьева.
Математика. Занятия школьного кружка.
5 –
6 классы – М. Издательство НЦ ЭНАС,2003.
• Е. В. Смыкалова. Сборник задач по математике для учащихся 6 класса. СМиО Пресс, 2003.
• В. Серпинский. Что мы знаем и чего не знаем о простых числах. ГИФ-МЛ, Москва 1963.__
• Е. В. Смыкалова. Сборник задач по математике для учащихся 6 класса. СМиО Пресс, 2003.
• В. Серпинский. Что мы знаем и чего не знаем о простых числах. ГИФ-МЛ, Москва 1963.__