С.В.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Использование теоремы Пифагора к решению задач.
Содержание
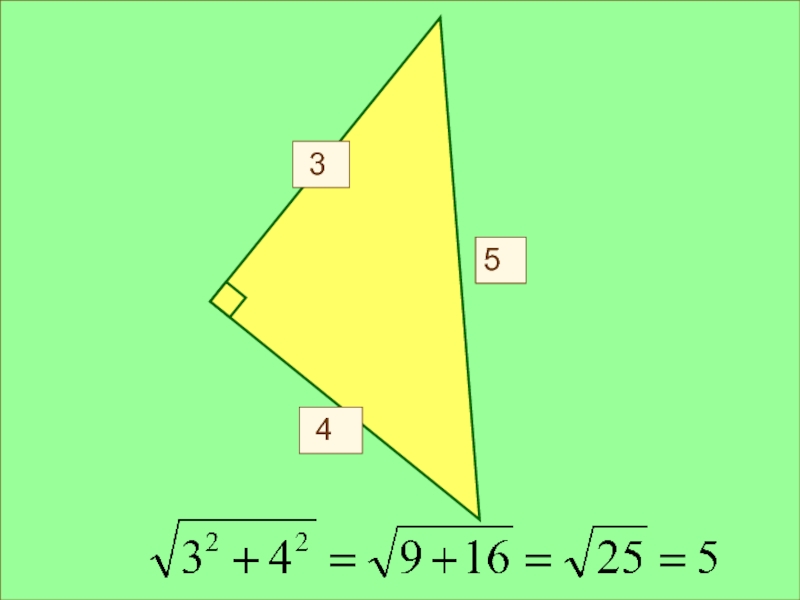
- 1. Использование теоремы Пифагора к решению задач.
- 2. СВА43Ответ: 6
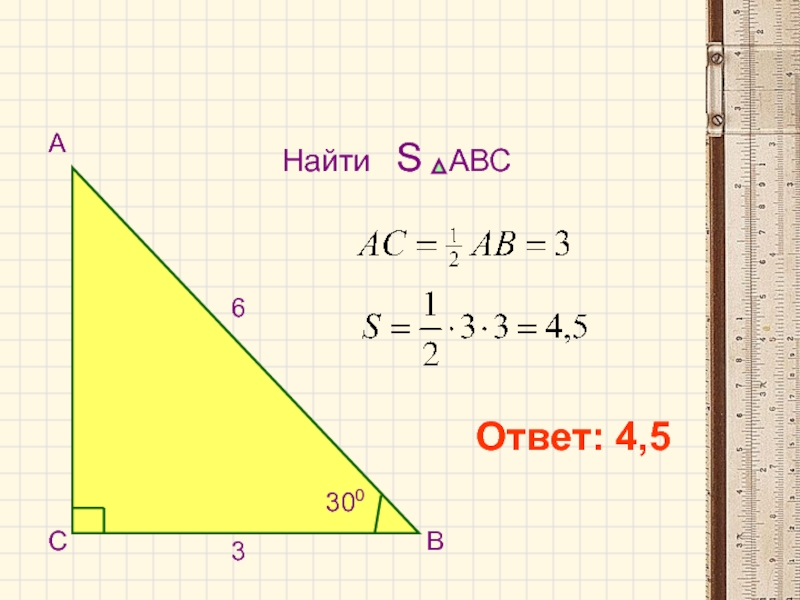
- 3. СВА3 3006Ответ: 4,5
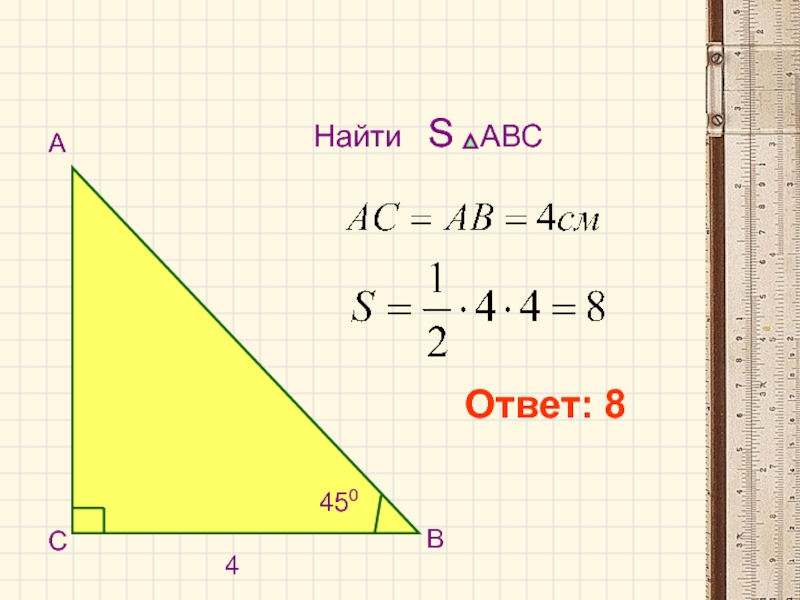
- 4. СВА4 450Ответ: 8
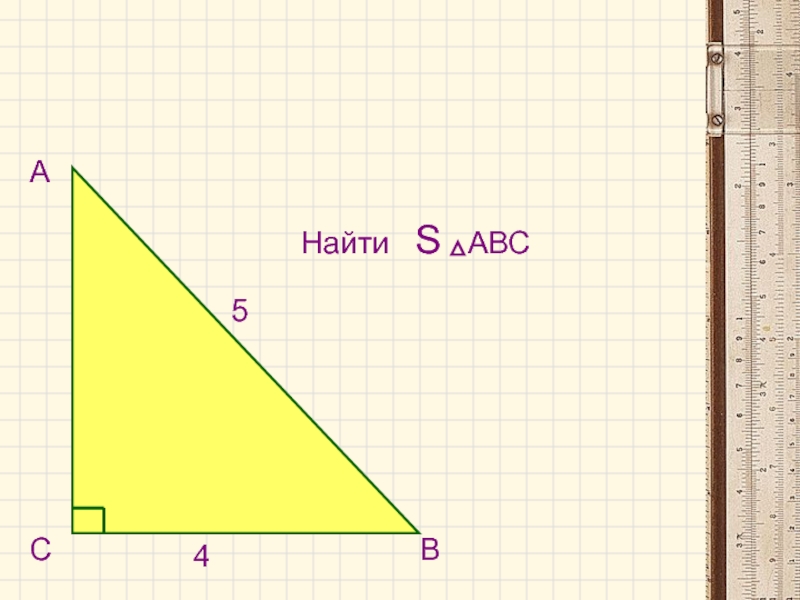
- 5. СВ4А5
- 6. Существует ли связь между гипотенузой и катетами прямоугольного треугольника?Да, существует!
- 7. Теорема Пифагора Пифагор – человек - легенда
- 8. Пифагор Самосский Считается, что Пифагор родился в
- 9. Пифагор -легендаФигура Пифагора была окружена множеством легенд:его
- 10. Пифагор – первый из философов
- 11. «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора»
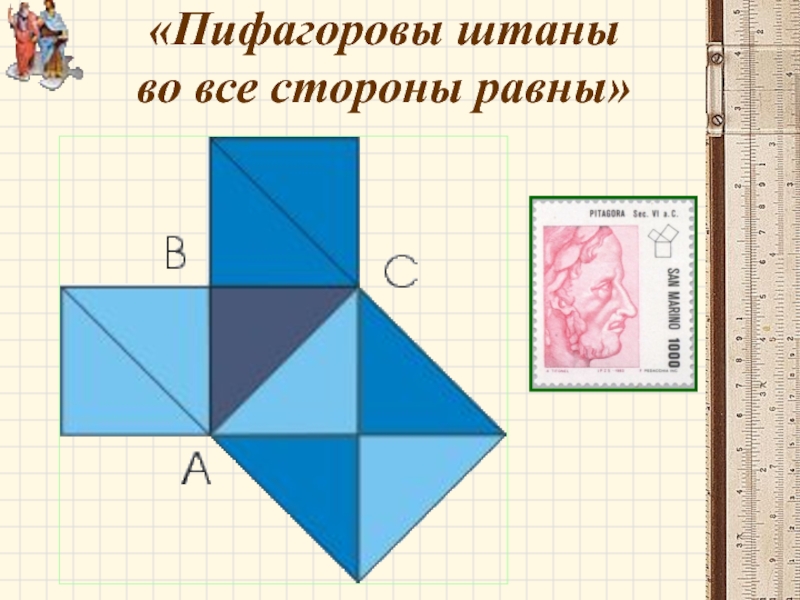
- 12. «Пифагоровы штаны во все стороны равны»
- 13. Во времена Пифагора формулировка теоремы звучала так:«Квадрат,
- 14. Существует более 100 различных доказательств теоремы Пифагора
- 15. История открытия теоремы Обычно открытие теоремы
- 16. аcbДано:Доказать:c2=a2+b2aaaabbbcccТаким образом, Один из способов доказательства теоремы cb
- 17. Доказательство теоремы Пифагора по Басхари ИллюстрируетДоказательствовеликого индийскогоматематика Басхаририсунок, с однимлишь словом:СМОТРИ!
- 18. Метод ГофманаПостроим треугольник ABC с прямым углом
- 19. Метод МёльманнаПлощадь данного прямоугольника с одной стороны
- 20. «В прямоугольном треугольнике квадратгипотенузы равен сумме квадратов катетов».cabТеорема Пифагора
- 21. Х 3 45
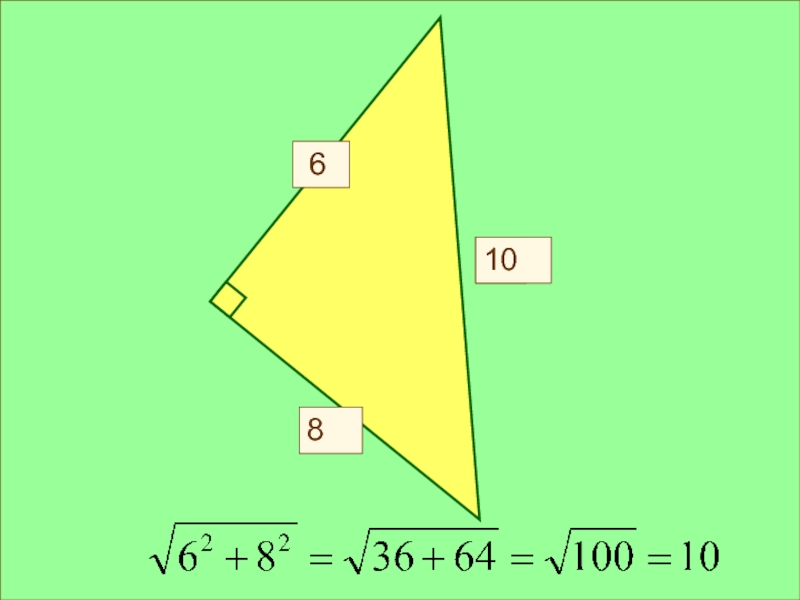
- 22. Х 6810
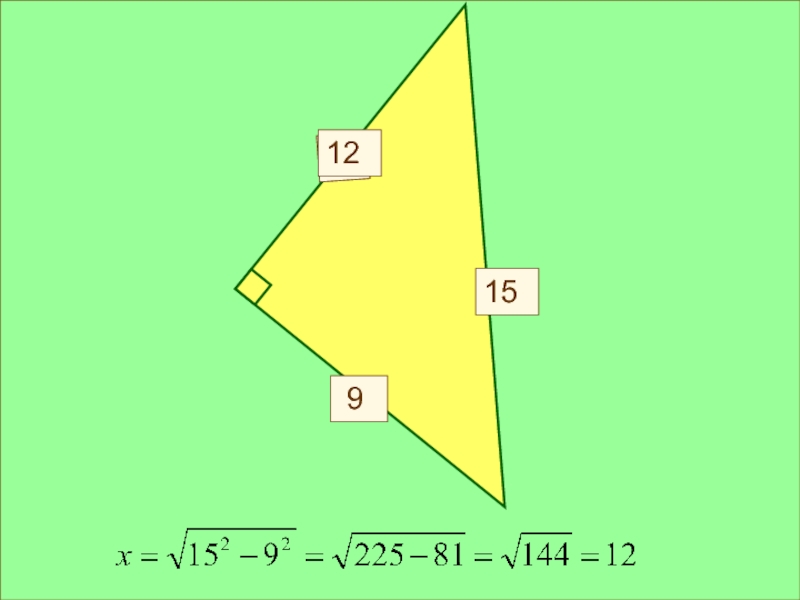
- 23. Х 91512
- 24. Пифагоровы треугольники Прямоугольные треугольники, у которых
- 25. Формулировка теоремы, обратной теореме ПифагораЕсли квадрат одной
- 26. Определите Какой треугольник является прямоугольным?13 м; 5
- 27. Если дан нам треугольникИ притом с прямым
- 28. Решение практических задач
- 29. Древнерусская задачаСлучися некоему человеку к стене лествицу
- 30. Тополь у реки«На береге реки рос тополь
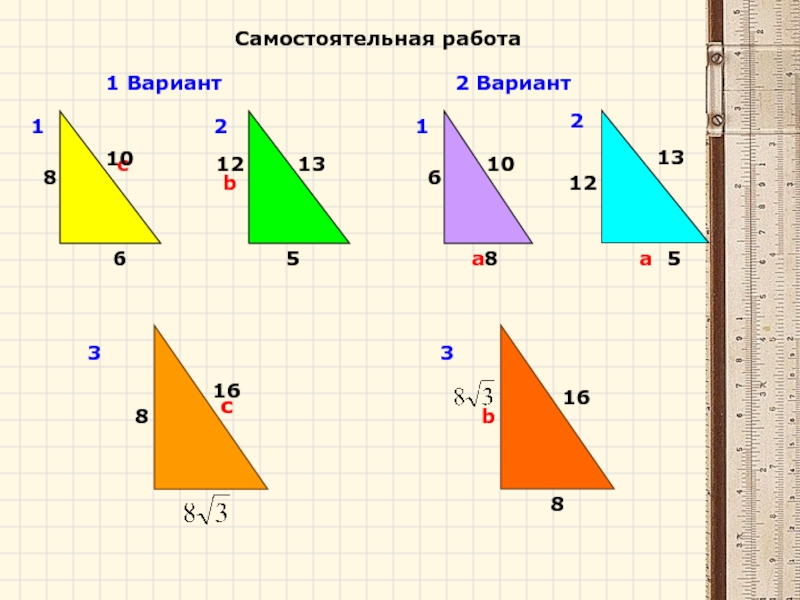
- 31. Самостоятельная работа 1 Вариант2 Вариант610a86c5131312ba1212c8b3316810128516
- 32. Итоги урока: ABCabcЕсли , то Если , то
- 33. Домашнее задание: п. 54, 55, вопросы 8
- 34. Спасибо за урок!
СВА43Ответ: 6
Слайд 8Пифагор Самосский
Считается, что Пифагор родился в аристократической семье на острове
Самос в Эгейском море у берегов Малой Азии. В детстве он получил превосходное образование. Чтобы постичь премудрости других народов он путешествовал по странам восточной части Средиземного моря, Египту и Вавилону.
Слайд 9Пифагор -легенда
Фигура Пифагора была окружена множеством легенд:
его считали перевоплощенным богом Аполлоном;
полагали,
что у него было золотое ребро;
он был способен преподавать в одно и то же время в двух местах;
он мог «вызвать затмение»
при помощи цифр…изгнать болезнь
он был способен преподавать в одно и то же время в двух местах;
он мог «вызвать затмение»
при помощи цифр…изгнать болезнь
Слайд 10 Пифагор – первый из философов своего времени удостоился, чтобы
портрет его появился на древних монетах
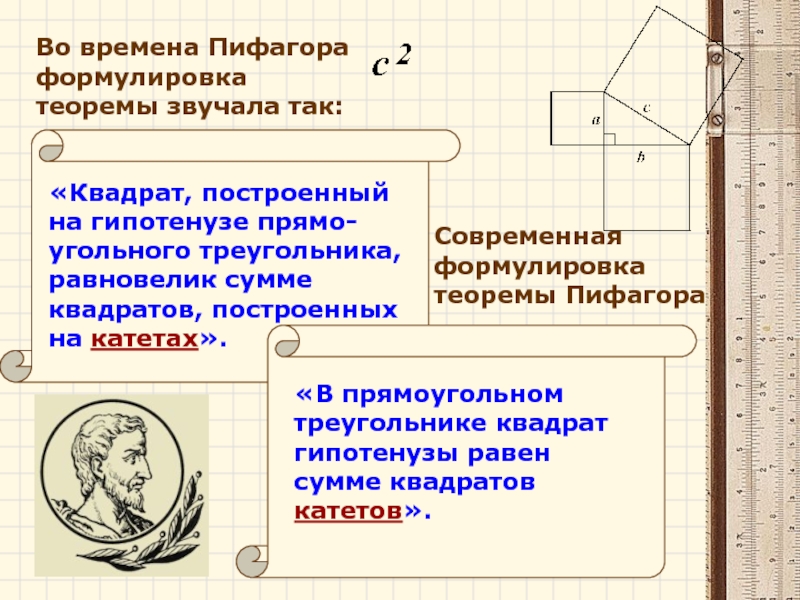
Слайд 13Во времена Пифагора формулировка теоремы звучала так:
«Квадрат, построенный на гипотенузе прямо-угольного
треугольника, равновелик сумме квадратов, построенных на катетах».
Современная формулировка
теоремы Пифагора
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов катетов».
Слайд 14Существует более 100 различных доказательств теоремы Пифагора
( геометрических, алгебраических, механических
и т.д.)
Теорема Пифагора занесена в книгу рекордов Гиннеса.
Теорема Пифагора занесена в книгу рекордов Гиннеса.
Слайд 15История открытия теоремы
Обычно открытие теоремы Пифагора приписывают Пифагору. Но
изучение вавилонских клинописных таблиц и древнекитайских рукописей показало, что это утверждение было известно задолго до Пифагора. Заслуга Пифагора в том, что он открыл доказательство этой теоремы.
Слайд 16
а
c
b
Дано:
Доказать:
c2=a2+b2
a
a
a
a
b
b
b
c
c
c
Таким образом,
Один из способов доказательства теоремы
c
b
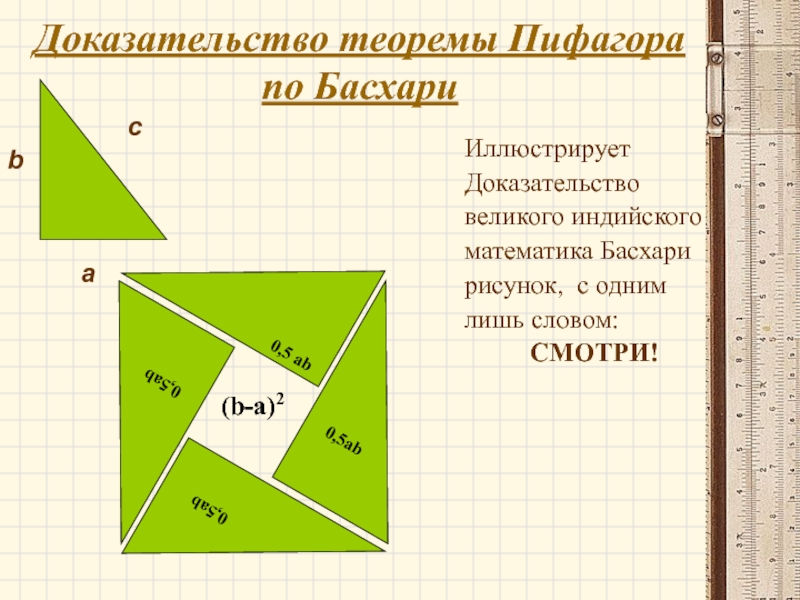
Слайд 17Доказательство теоремы Пифагора по Басхари
Иллюстрирует
Доказательство
великого индийского
математика Басхари
рисунок, с одним
лишь словом:
СМОТРИ!
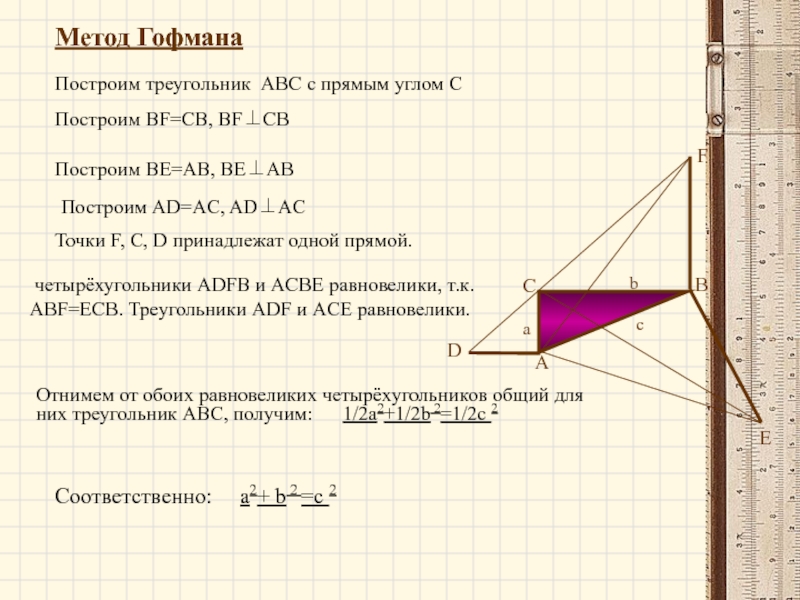
Слайд 18Метод Гофмана
Построим треугольник ABC с прямым углом С
Построим BF=CB, BF⊥CB
Построим
BE=AB, BE⊥AB
Построим AD=AC, AD⊥AC
Точки F, C, D принадлежат одной прямой.
четырёхугольники ADFB и ACBE равновелики, т.к. ABF=ЕCB. Треугольники ADF и ACE равновелики.
Отнимем от обоих равновеликих четырёхугольников общий для них треугольник ABC, получим: 1/2а2+1/2b 2=1/2с 2
Соответственно: а2+ b 2 =с 2
Слайд 19Метод Мёльманна
Площадь данного прямоугольника с одной стороны равна 0.5ab, с другой
0.5pr, где p – полупериметр треугольника, r – радиус вписанной в него окружности (r = 0.5(a+b-c))
Имеем:
0.5ab=0.5pr=0.5(a+b+c)*0.5(a+b-c)
Отсюда следует , что
с2=а2+b2
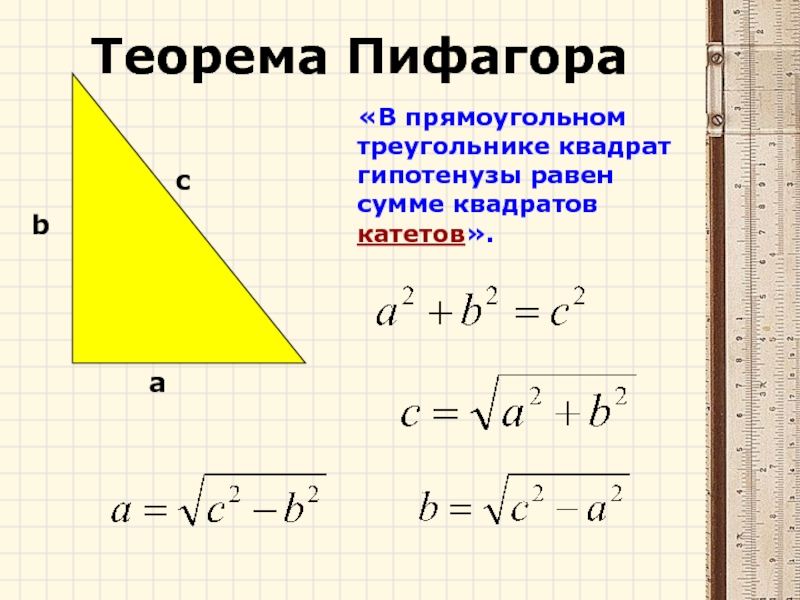
Слайд 20«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов катетов».
c
a
b
Теорема Пифагора
Слайд 24Пифагоровы треугольники
Прямоугольные треугольники, у которых длины сторон треугольников выражаются
целыми числами называются пифагоровыми треугольниками
Примеры: 3, 4, 5
5, 12, 13;
8, 15, 17
7, 24, 25
Треугольник со сторонами 3, 4, 5
называют египетским треугольником
Примеры: 3, 4, 5
5, 12, 13;
8, 15, 17
7, 24, 25
Треугольник со сторонами 3, 4, 5
называют египетским треугольником
Слайд 25Формулировка теоремы, обратной теореме Пифагора
Если квадрат одной стороны треугольника
равен сумме
квадратов двух других сторон,
то треугольник прямоугольный.
то треугольник прямоугольный.
Слайд 27Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда
легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придем.
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придем.
И. Дырченко
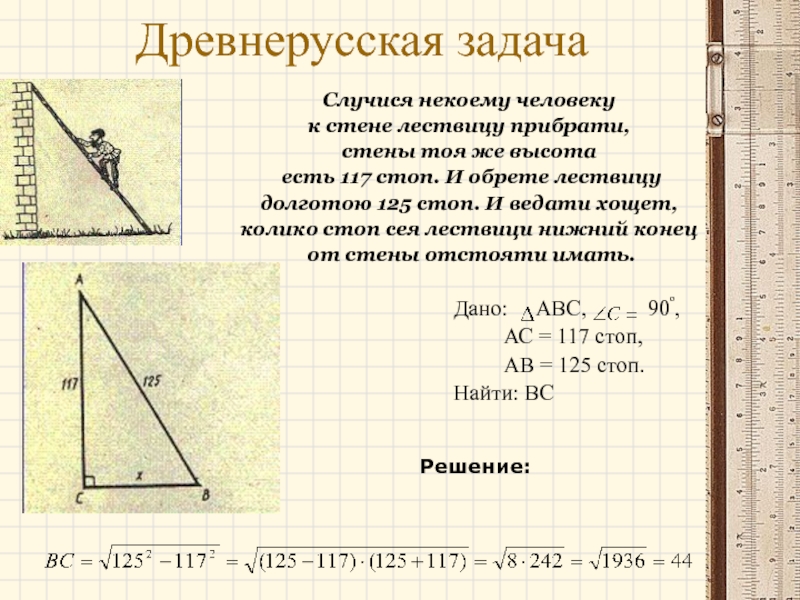
Слайд 29Древнерусская задача
Случися некоему человеку
к стене лествицу прибрати,
стены тоя же
высота
есть 117 стоп. И обрете лествицу
долготою 125 стоп. И ведати хощет,
колико стоп сея лествици нижний конец
от стены отстояти имать.
Дано: АВС, 90º,
АС = 117 стоп,
АВ = 125 стоп.
Найти: ВС
есть 117 стоп. И обрете лествицу
долготою 125 стоп. И ведати хощет,
колико стоп сея лествици нижний конец
от стены отстояти имать.
Дано: АВС, 90º,
АС = 117 стоп,
АВ = 125 стоп.
Найти: ВС
Решение:
Слайд 30Тополь у реки
«На береге реки рос тополь одинокий.
Вдруг ветра порыв его
ствол надломал.
Бедный тополь упал. И угол прямой
С течением реки его угол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Дано: АС = 3 фута, AD = 4 фута,
BC = CD.
Найти: АВ.
Бедный тополь упал. И угол прямой
С течением реки его угол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Дано: АС = 3 фута, AD = 4 фута,
BC = CD.
Найти: АВ.
Решение:
AB=AC+CB=AC+CD.
CD=
AB=5+3=8
ACD,
