- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Интересные факты о треугольниках. Мини-учебник для учащихся и преподавателей.
Содержание
- 1. Интересные факты о треугольниках. Мини-учебник для учащихся и преподавателей.
- 2. Содержание- Проверь себя- Тесты- Терминологический словарьвыход
- 3. Треугольник - первая геометрическая фигура, встречающаяся в
- 4. В герметической идеографии треугольник с устремленной к
- 5. Ацтеки использовали изображение треугольника с вершиной наверху,
- 6. Светящаяся Дельта - это равнобедренный треугольник (с
- 7. Если у треугольника три неравные стороны,
- 8. Прямоугольным называется тот треугольник, у которого один
- 9. Если при построении педального треугольника углы получаются
- 10. Тогда Перепишем последнее равенство в таком виде:
- 11. Доказательство. Так как ВР=АР, то отрезок РМ
- 12. Следовательно, треугольник АМР подобен треугольнику СМА и
- 13. В равнобедренном треугольнике АРC высота PD является
- 14. 1) Основания перпендикуляров, опущенных из точки на
- 15. Сложив, получим
- 16. Доказательство: т.к. OL, OM, ON – перпендикуляры, то AO2-AL2=BO2-BL2 или Сложив эти три равенства, получим: AL2-BL2+BM2-MC2+CN2-NA2=0 или AL2+BM2+CN2=BL2+MC2+NA2.3)
- 17. Доказательство: Если соединить точки А и Р, то получим
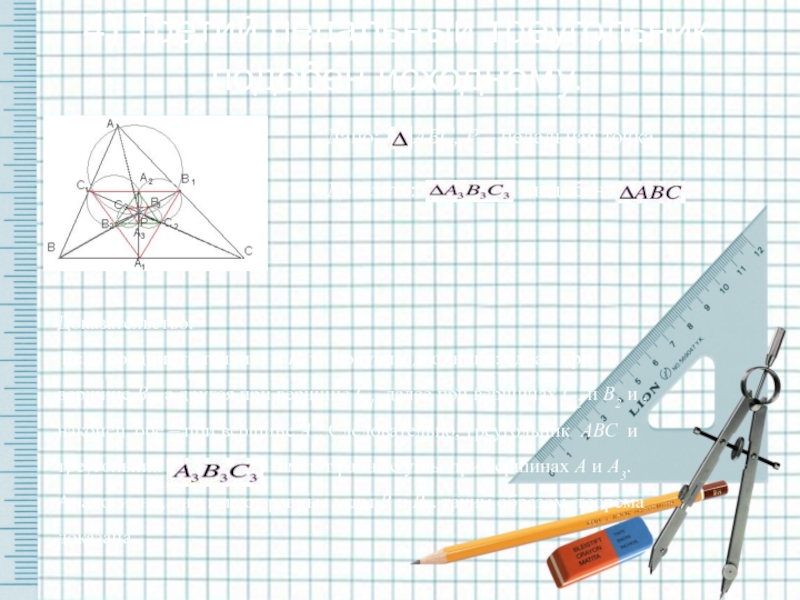
- 18. Вычисление площади педального треугольника.Тогда SА1В1С1= SС1МВ1 +
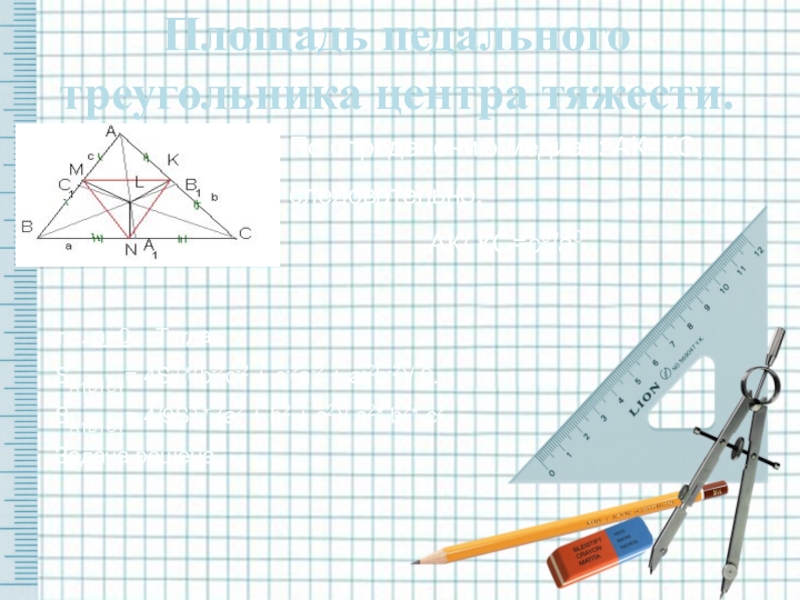
- 19. Площадь педального треугольника центра тяжести.т.е. n=0.
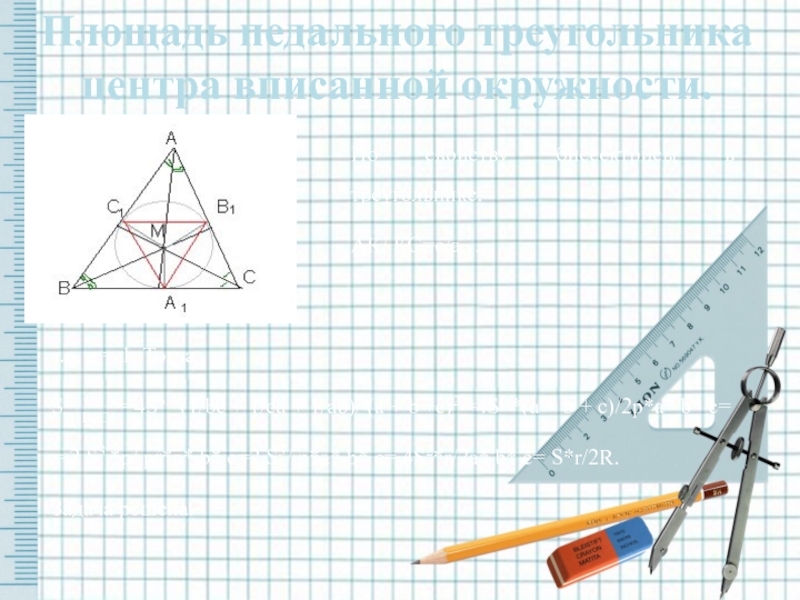
- 20. Площадь педального треугольника центра вписанной окружности. По
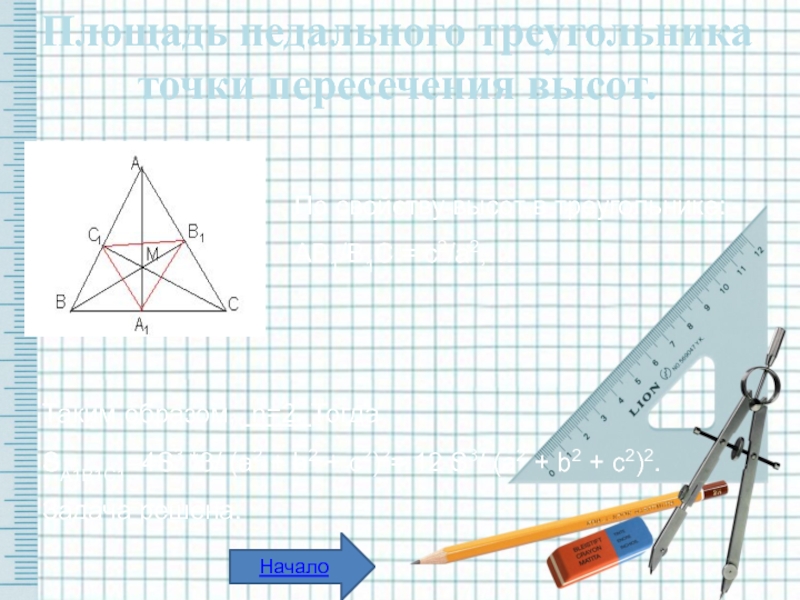
- 21. Площадь педального треугольника точки пересечения высот.По свойству
- 22. Проверь себя
- 23. Решение: Ответ: 7,5 (см)Задача 1 Вычислить стороны
- 24. Дано: АВС – равносторонний, la=1,5 см, lb=2,8 см, lc=1,7 см. Найти:
- 25. Дано: треугольник АВС; OL, OM и ON - перпендикуляры
- 26. Решение.
- 27. Решение. Ответ: Задача 5Определите угол Брокара, если треугольник имеет следующие стороны 3, 2 и 5.
- 28. Решение. В прямоугольном треугольнике DCB
- 29. Слайд 29
- 30. Три точки, образующие треугольник, называются Вершинами треугольникаТочками БрокараСторонами треугольникаГлавными точками
- 31. Стороны треугольника образуют в вершинах треугольникаТри углаплоскостьУголотрезок
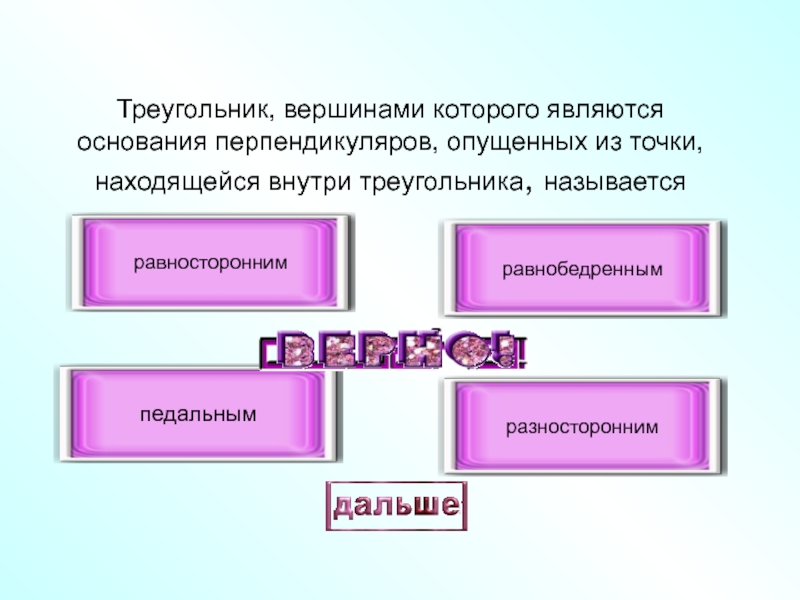
- 32. Треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки, находящейся внутри треугольника, называетсяпедальнымравностороннимравнобедреннымразносторонним
- 33. Точкой Брокара называется точка, которая при соединении с
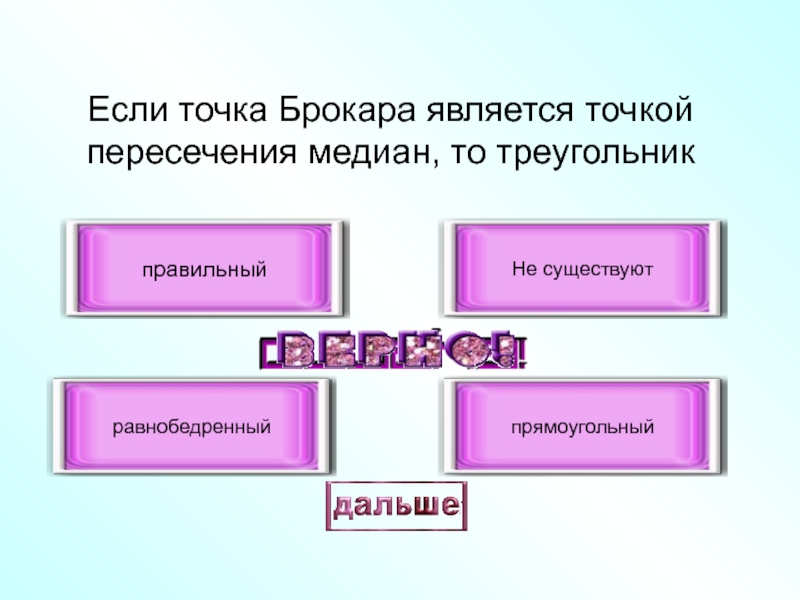
- 34. Если точка Брокара является точкой пересечения медиан, то треугольникправильныйравнобедренныйНе существуютпрямоугольный
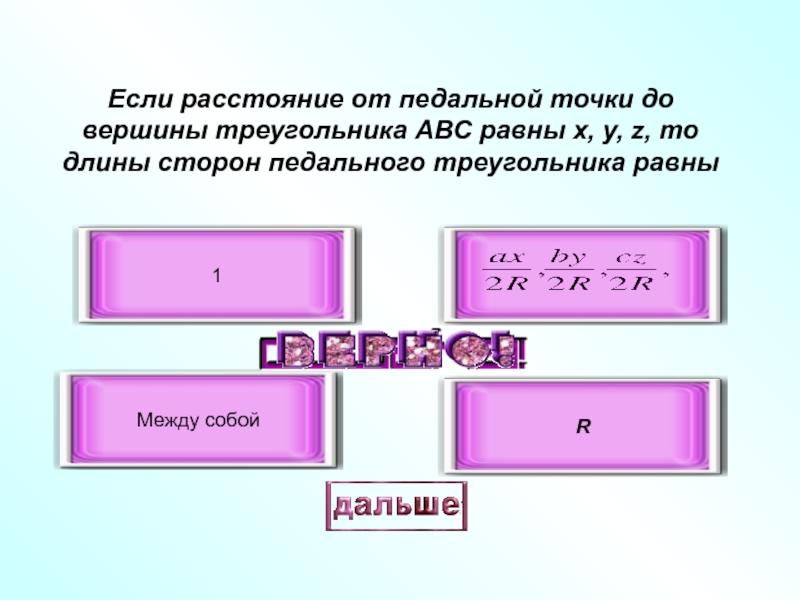
- 35. Если расстояние от педальной точки до вершины
- 36. Начало
- 37. Терминологический словарьПедальный треугольник - треугольник, вершинами которого
- 38. Слайд 38
Слайд 3Треугольник - первая геометрическая фигура, встречающаяся в древних орнаментах.
Интересные факты
В Египте
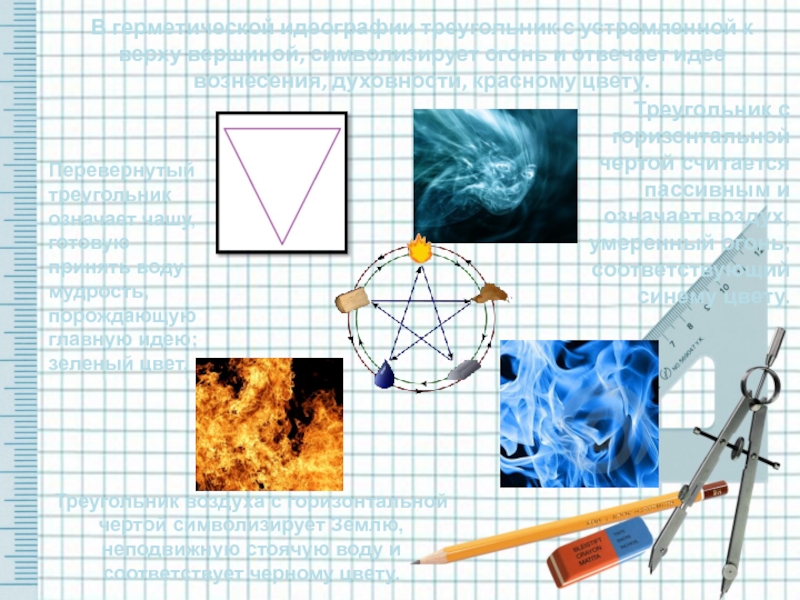
Слайд 4В герметической идеографии треугольник с устремленной к верху вершиной, символизирует огонь
Треугольник с горизонтальной чертой считается пассивным и означает воздух, умеренный огонь, соответствующий синему цвету.
Перевернутый треугольник означает чашу, готовую принять воду; мудрость, порождающую главную идею; зеленый цвет.
Треугольник воздуха с горизонтальной чертой символизирует Землю, неподвижную стоячую воду и соответствует черному цвету.
Слайд 5Ацтеки использовали изображение треугольника с вершиной наверху, соединенного с перевернутым треугольником,
Треугольник в сочетании с крестом образует алхимический знак Серы.
Равносторонний треугольник, символизирующий, по древнееврейской традиции, совершенство, у христиан означает Троицу - Отца, Сына и Святого Духа.
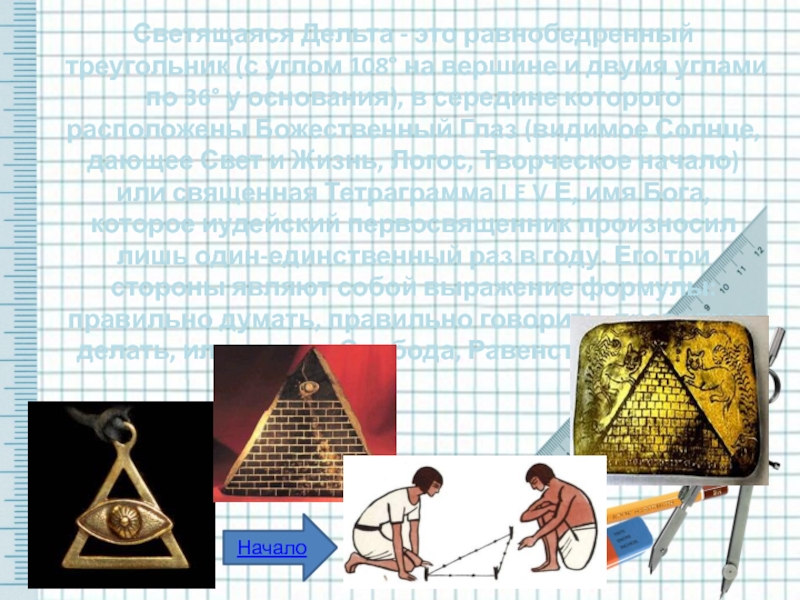
Слайд 6Светящаяся Дельта - это равнобедренный треугольник (с углом 108° на вершине
Начало
Слайд 7 Если у треугольника три неравные стороны, то это разносторонний треугольник.(а)
если три равные стороны, то равносторонний треугольник.(б)
В равнобедренном треугольнике углы, лежащие против равных сторон, равны; в равностороннем треугольнике все углы равны.(в)
Виды треугольников
а)
б)
в)
Слайд 8Прямоугольным называется тот треугольник, у которого один из углов прямой. Сторона,
Начало
Слайд 9Если при построении педального треугольника углы получаются равными, то они называются
Чтобы построить точку Брокара, надо провести окружность через две вершины треугольника АВС, затем прямую, параллельную противоположной стороне выбранной вершины. Соединим третью вершину с точкой пересечения параллельной прямой и окружности. Эта прямая пересечет окружность внутри треугольника. Точка пересечения будет является точкой Брокара.
Угол Брокара определяется по формуле
,
а площадь педального треугольника точки Брокара равна
Пусть Р – любая точка внутри данного треугольника АВС, и пусть перпендикуляры, опущенные из точки Р на стороны ВС, СА, АВ треугольника, будут РА1, РВ1 и РС1. треугольник А1В1С1, вершинами которого являются основания этих перпендикуляров, называется педальным треугольником треугольника АВС для «педальной точки» Р.
Педальный треугольник
Слайд 10Тогда
Перепишем последнее равенство в таком виде:
Из этой пропорции
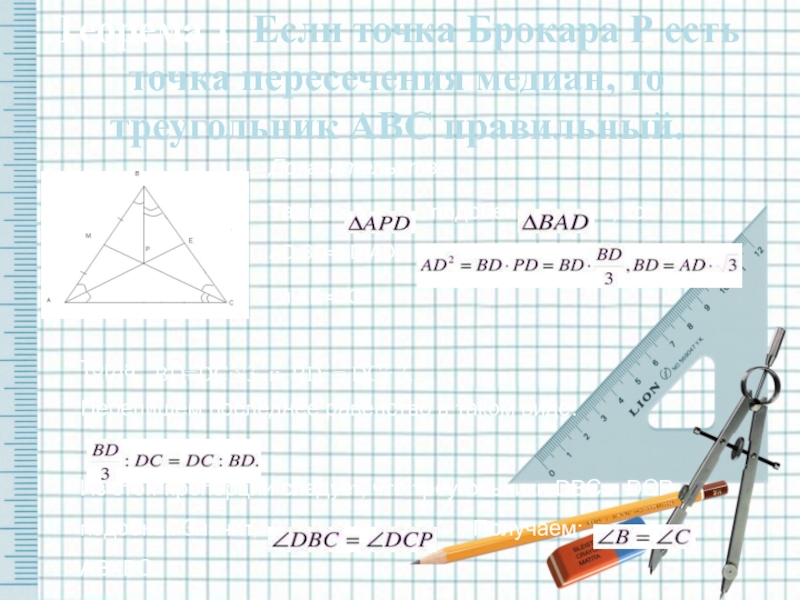
Доказательство.
Так как подобен , то AD:BD=PD:AD,
и AD=DC.
Теорема 1. Если точка Брокара Р есть точка пересечения медиан, то треугольник АВС правильный.
BD=DC∙√3 и BD2 = DC2. 3.
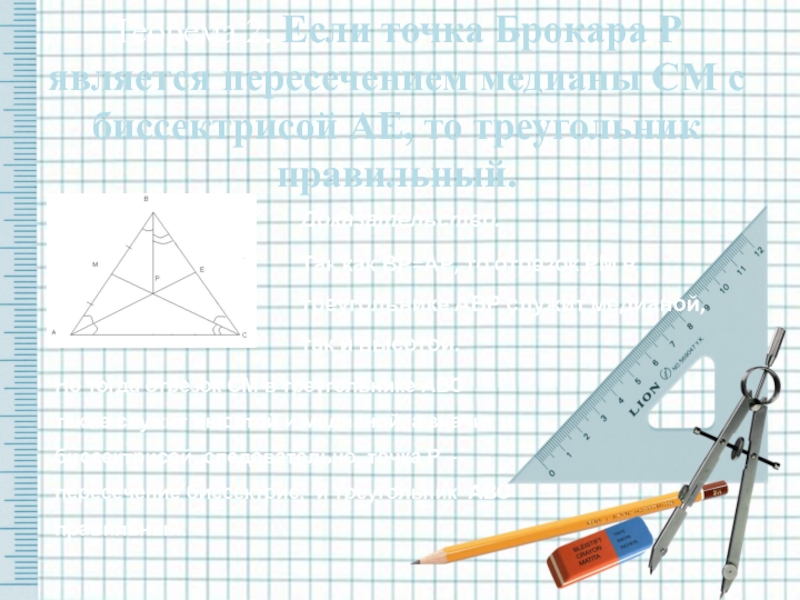
Слайд 11Доказательство.
Так как ВР=АР, то отрезок РМ в треугольнике АВР служит
Теорема 2. Если точка Брокара Р является пересечением медианы СМ с биссектрисой АЕ, то треугольник правильный.
Но тогда отрезок СМ в треугольнике АВС также служит высотой и медианой, а значит и биссектрисой, следовательно, точка Р – пересечение биссектрис, и треугольник АВС правильный.
Слайд 12Следовательно, треугольник АМР подобен треугольнику СМА и угол МАР равен углу
Доказательство.
Из подобия треугольников МВР и МСВ следует, что МВ:МС=МР:МВ или МВ2=МС.МР, но по условию МВ=МА, тогда МА2=МС.МР и МА:МС=МР:МА.
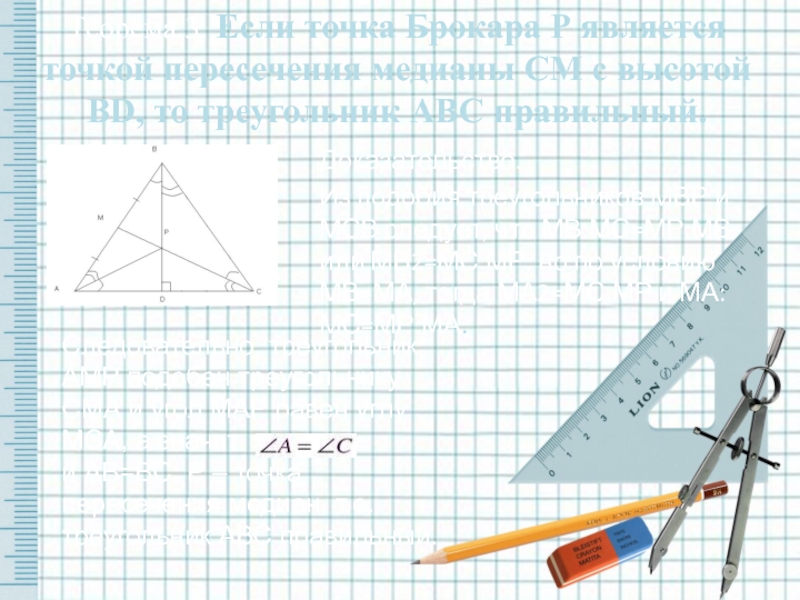
Теорема 3. Если точка Брокара Р является точкой пересечения медианы СМ с высотой ВD, то треугольник АВС правильный.
Слайд 13В равнобедренном треугольнике АРC высота PD является и медианой, т.е. AD=DC.
Доказательство.
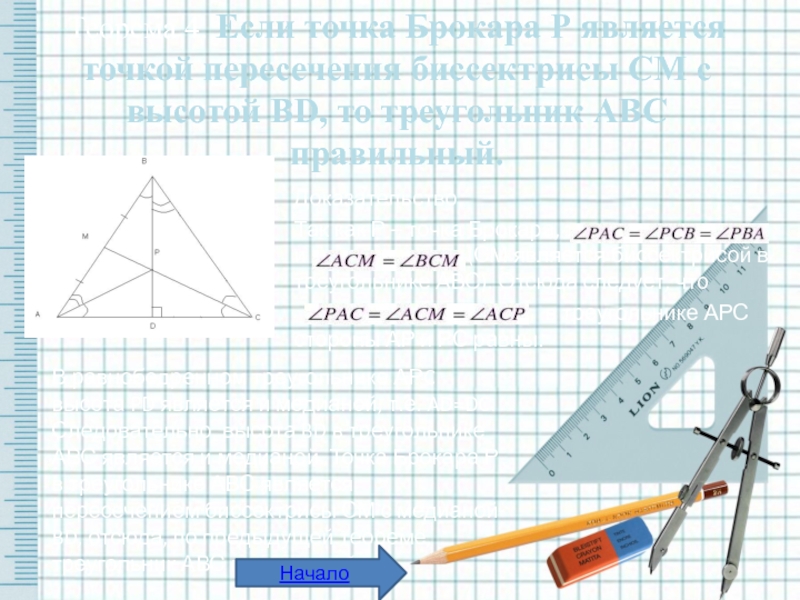
Так как Р – точка Брокара, то и (СМ является биссектрисой в треугольнике АВС). Отсюда следует, что
в треугольнике АРС стороны АР и РС равны.
Теорема 4. Если точка Брокара Р является точкой пересечения биссектрисы СМ с высотой BD, то треугольник АВС правильный.
Начало
Слайд 141) Основания перпендикуляров, опущенных из точки на стороны треугольника, лежат на
Практическая часть
Прямая, содержащая эти основания, известна как прямая Симсона данной точки относительно данного треугольника. Прямая Симсона приписывалась ему, поскольку она казалась типичной для его геометрических идей. Однако историки тщетно пытались найти ее в его работах. В действительности она была открыта в 1797 году Вильямом Уоллесом.
Слайд 15Сложив, получим
.
Следствие. В равностороннем треугольнике сумма расстояний от произвольной точки, взятой внутри треугольника, до его сторон есть величина постоянная, равная высоте треугольника.
Имеем: .
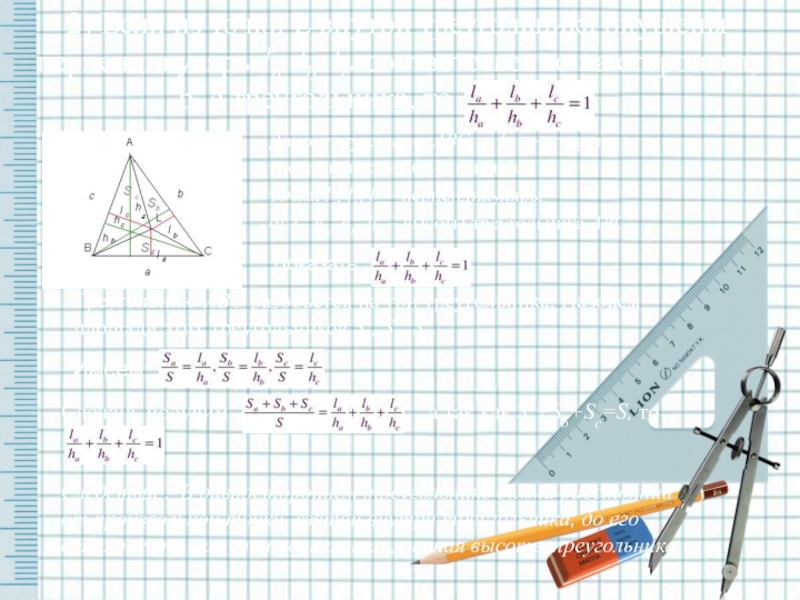
2) Если из точки L внутри треугольника опущены перпендикуляры соответственно на стороны а, b, с треугольника, то .
la, lb, lc,
Дано: треугольник АВС, а, b, с – стороны треугольника АВС, – педальная точка, la, lb, lc – перпендикуляры от L, ha, hb, hc – высоты треугольника АВС.
Доказать:
Треугольник АВС разобьется на три треугольника. Назовем площади этих треугольников Sa, Sb, Sc.
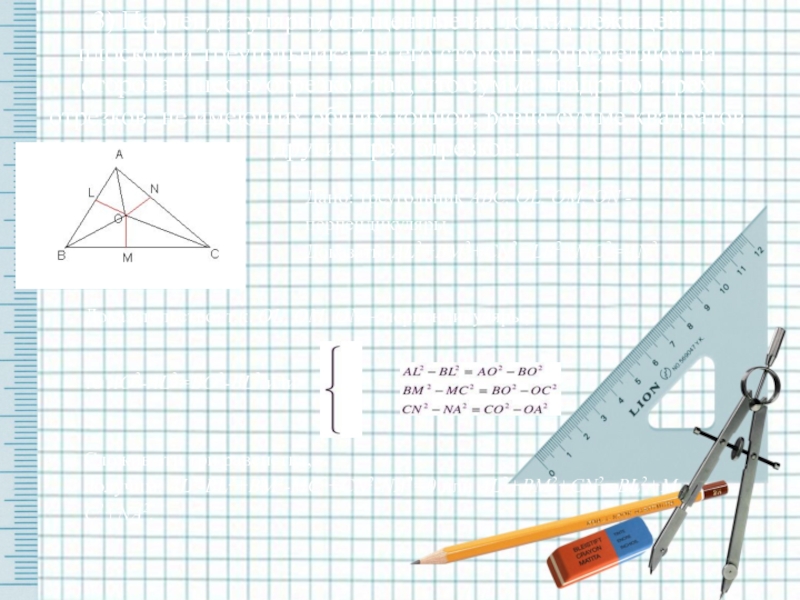
Слайд 16Доказательство: т.к. OL, OM, ON – перпендикуляры,
то AO2-AL2=BO2-BL2 или
Сложив эти три равенства, получим: AL2-BL2+BM2-MC2+CN2-NA2=0 или AL2+BM2+CN2=BL2+MC2+NA2.
3) Перпендикуляры, опущенные их точки, лежащей
Дано: треугольник АВС, OL, OM, ON - перпендикуляры.
Доказать: AL2+BM2+CN2=LB2+MC2=AN2
Слайд 17Доказательство:
Если соединить точки А и Р, то получим двойники: одна - при
Дано: АВС, Р – педальная точка.
Доказать: подобен
4) Третий педальный треугольник подобен исходному.
Слайд 18Вычисление площади педального треугольника.
Тогда SА1В1С1= SС1МВ1 + SA1MB1= SA1MC.
Так как данный
SС1МВ1 = S*С1М* МВ1 / c* b.
Так как С1М= 2S*сn-1/(an + bn +cn), МВ1= 2S*bn-1/(an + bn +cn), A1M= 2S*an-1/(an + bn +cn),
то SА1В1С1= 4S3 * сn-1* bn-1/(an + bn +cn)2* c* b= 4S3 * сn-2* bn-2/(an + bn +cn)2 .
Определив аналогично площади треугольников A1M В1 и A1M С1 и сложив полученные значения, найдём площадь педального треугольника:
SА1В1С1= 4S3 *(bn-2cn-2 + cn-2an-2 + an-2bn-2)/ (an + bn +cn)2 .
Задача решена.
Пусть М- точка пересечения прямых n, т.е. прямых, делящих стороны треугольника пропорционально n-м степеням прилежащих сторон, и А1С1В1– медальный треугольник точки М .
Слайд 19Площадь педального треугольника центра тяжести.
т.е. n=0. Тогда
SА1В1С1= 4S3 *(b-2c-2 +
SА1В1С1= 4/9S3 * (a2 + b2 + c2)/ a2* b2* c2.
Задача решена.
По определению медиан: АК=КС, следовательно:
АК/ КС=с0/а0,…
Слайд 20Площадь педального треугольника центра вписанной окружности.
По свойству биссектрисы в треугольнике:
АК/ КС=с/а,…
т.е. n = 1. Тогда
SА1В1С1= 4S3 *(1/bc + 1/ca + 1/ab)/ (a + b +c)2 =4S3 *(a + b + c)/2р*a* b* c=
= 2 S3 *р/ р2*a* b* c=2 S3/ р*a* b* c= 4S2*r/2a* b* c= S*r/2R.
Задача решена.
Слайд 21Площадь педального треугольника точки пересечения высот.
По свойству высот в треугольнике:
АВ1/В1С
Таким образом, n=2. Тогда
SА1В1С1=4S3 *3/ (a2 + b2 + c2)2= 12 S3/ (a2 + b2 + c2)2.
Задача решена.
Начало
Слайд 23Решение:
Ответ: 7,5 (см)
Задача 1
Вычислить стороны педального треугольника, если
Слайд 24Дано:
АВС – равносторонний, la=1,5 см, lb=2,8 см, lc=1,7 см.
Найти:
Решение:
Т.к. треугольник равносторонний, то la+lb+lc=h, т.е. h=1,5+2,8+1,7=6
(см).
Пусть ВD=х, АВ=36+х2=4х2 ,
36=3х2 ,
х2=12,
(см2) Ответ. 12 (см2) .
Задача 2
Расстояния от точки треугольника, взятой внутри равностороннего треугольника АВС, до сторон АВ, ВС, АС равны соответственно 1,7 см, 2,8 см, 1,5 см. Найти площадь этого треугольника.
Слайд 25Дано: треугольник АВС; OL, OM и ON - перпендикуляры
Т.к.
, а АВ=9, то AL=3, LB=9,
аналогично, AN=3, NC=12.
По теореме о сумме отрезков AL2+BM2+CN2=BL2+MC2+AN2 , 9+64+144=81+МС2+9,
МС2=127,
МС= ,
ВС=8+ (см)
Ответ: 8+ (см)
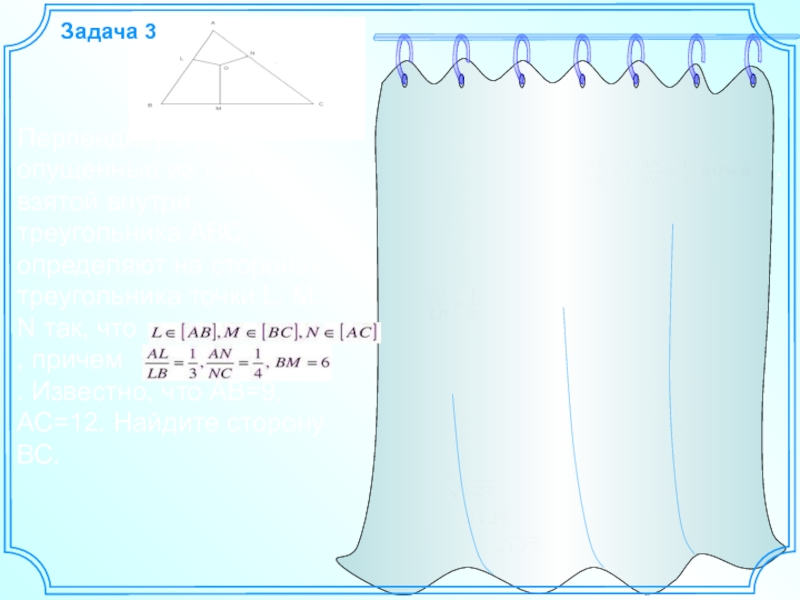
Задача 3
Перпендикуляры, опущенные из точки О, взятой внутри треугольника АВС, определяют на сторонах треугольника точки L, M, N так, что , причем . Известно, что АВ=9, АС=12. Найдите сторону ВС.
Слайд 26Решение.
Ответ: 1,57 (см2)
Задача 4
Найти площадь педального треугольника точки Брокара, если стороны треугольника равны 4, 7 и 5 см.
Слайд 27Решение.
Ответ:
Задача 5
Определите угол Брокара, если треугольник имеет следующие
Слайд 28Решение.
В прямоугольном треугольнике DCB
и подставив в нее это равенство, получаем:
.
Выполним преобразования:
где 2sinAsinC=cos(C-A)-cos(C+A).
Подставив в формулу это значение, получаем:
Подставив значения косинуса угла В, получим:
Учитывая, что , находим:
В первом случае:
Во втором случае:
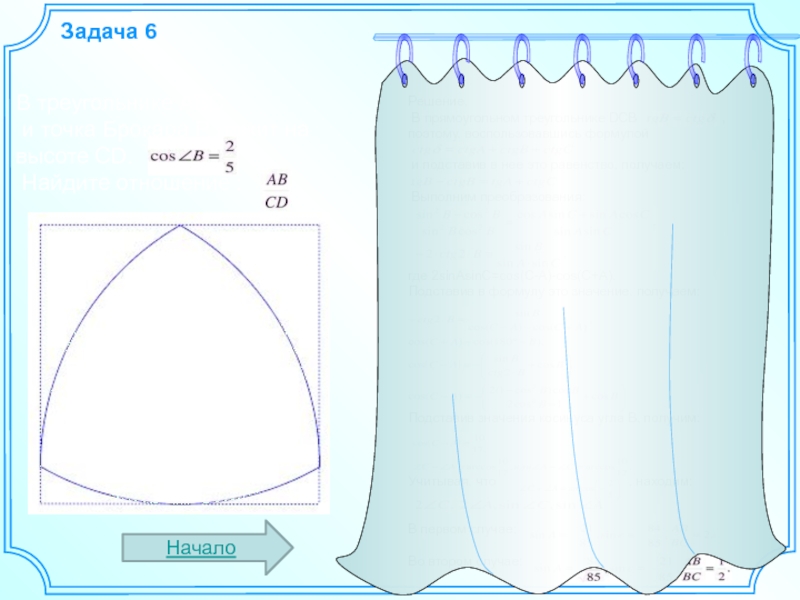
Задача 6
В треугольнике АВС
и точка Брокара Р лежит на высоте CD.
Найдите отношение :
Начало
Слайд 30Три точки, образующие треугольник, называются
Вершинами треугольника
Точками Брокара
Сторонами треугольника
Главными точками
Слайд 32Треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки, находящейся внутри
педальным
равносторонним
равнобедренным
разносторонним
Слайд 33Точкой Брокара называется
точка, которая при соединении
с вершинами треугольника образует
равные
Точка пересечения
медиан треугольника
центр окружности
главная точка
Слайд 34Если точка Брокара является точкой пересечения медиан, то треугольник
правильный
равнобедренный
Не существуют
прямоугольный
Слайд 35Если расстояние от педальной точки до вершины треугольника АВС равны х,
Между собой
1
R
Слайд 37Терминологический словарь
Педальный треугольник - треугольник, вершинами которого является основания перпендикуляров, опущенных
Если педальную точку взять на описанной окружности, то основания перпендикуляров, опущенных от данной точки к сторонам треугольника лежат на одной прямой, которая называется прямой Симсона.
Точкой Брокара называется такая педальная точка, которая при соединении с вершинами треугольника образует равные чередующиеся углы. А такие углы называются углами Брокара.
Начало