- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему интеграл
Содержание
- 1. интеграл
- 2. Содержание Введение 1. История интегрального и дифференциального исчисления
- 3. Введение«Применение дифференциального и интегрального исчисления к решению физических
- 4. 1. История интегрального и дифференциального исчисления История понятия интеграла
- 5. Математики XVII столетия, получившие многие новые результаты,
- 6. Методы математического анализа активно развивались в следующем
- 7. 2. Дифференциал в физике Для вычисления дифференциала надо
- 8. Работа. Найдем работу, которую совершает заданная сила F при перемещении
- 9. 3. Приложения определенного интеграла к решению некоторых
- 10. 4. Дифференциальные уравненияМногие физические законы имеют вид
- 11. ПримерУравнение механического движения. Пусть материальная точка массы т движется под
- 12. 5. Примеры решения задач в matlabЗадача 1.
- 13. Программа:x=-2:0.1:2;title('{\itf(x)=x^{n}}');xlabel('x');ylabel('y');hFigure=gcf;set(hFigure,'Color',[1 1 1]);hText=text;set(hText,'FontSize',[18]);for n=2:4y=x.^n;hold onhPlot=plot(x,y);set(hPlot,'Color',[1.8/n 0.7 0.5]);set(hPlot,'LineWidth',2);if
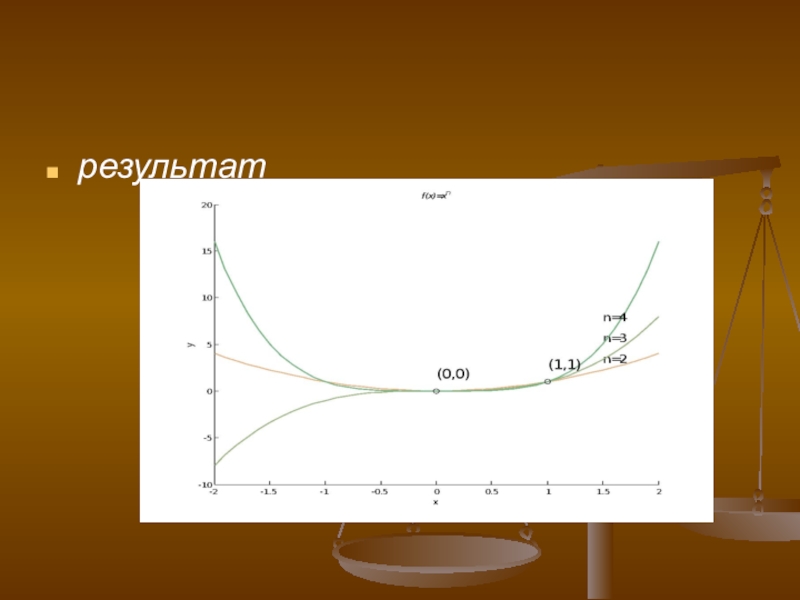
- 14. результат
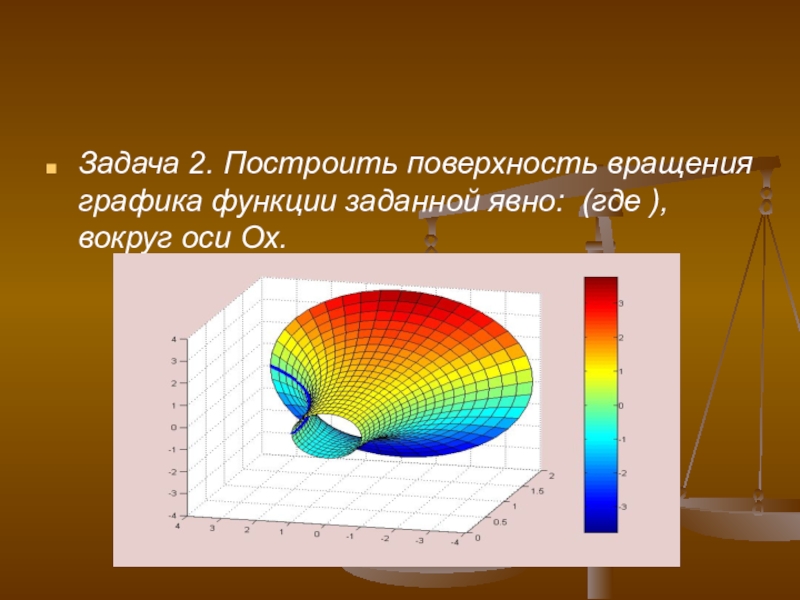
- 15. Задача 2. Построить поверхность вращения графика функции заданной явно: (где ), вокруг оси Ох.
- 16. Программа:x1=0; x2=2; a=1;u=x1:0.1:x2; v=0:pi/20:2*pi; [U,V]=meshgrid(u,v); F=a*(exp(-U/a)+exp(U/a))/2; X=U;
- 17. Список использованных источников Ануфриев, И.Е. Самоучитель MatLab
Слайд 2Содержание
Введение
1. История интегрального и дифференциального исчисления
2. Дифференциал в физике
3. Приложения определенного интеграла
Слайд 3Введение
«Применение дифференциального и интегрального исчисления к решению физических и геометрических задач» имеет
«Применение интегрального исчисления к решению физических и геометрических задач» углубляет материал курса алгебры и начал анализа в одиннадцатом классе и раскрывает возможности для практического закрепления материала по темам, входящим в школьный курс математики. Это темы «Производная функции», «Определённый интеграл» в алгебре, и некоторые темы в геометрии и физике . В результате данный факультативный курс реализует межпредметную связь алгебры и математического анализа с геометрией, информатикой и физикой.
Развитию у учащихся правильных представлений о характере отражения алгеброй основных элементов в геометрии и физике, роли математического моделирования в научном познании способствует знакомство их с решением и визуализацией различных математических задач на компьютере. Изложение факультативного курса базируется на основных возможностях версии 6.1 пакета математических и инженерных вычислений MATLAB, ставшего в настоящее время стандартным средством поддержки изучения высшей математики, численного анализа и других учебных курсов во многих университетах. Учащимся излагаются основные возможности численных и символьных вычислений, программирования и визуализации результатов, предоставляемые ядром системы MATLAB и его пакета расширения Symbolic Math Toolbox.
Слайд 41. История интегрального и дифференциального исчисления
История понятия интеграла тесно связана с задачами
Многие значительные достижения математиков Древней Греции в решении задач на нахождение квадратур (т. е. вычисление площадей) плоских фигур, а также кубатур (вычисление объемов) тел связаны с применением метода исчерпывания, предложенным Евдоксом Книдским (ок. 408 -- ок. 355 до н.э.). Метод Евдокса был усовершенствован Архимедом (ок. 287 - 212 до н.э.). С этой модификацией вы знакомы: вывод формулы площади круга, предложенный в курсе геометрии, основан на идеях Архимеда
Его остроумные и глубокие идеи, связанные с вычислением площадей и объёмов тел, решением задач механики, по существу, предвосхищают открытие математического анализа и интегрального исчисления, сделанное почти 2000 лет спустя. Добавим, что практически и первые теоремы о пределах были доказаны им.
Слайд 5
Математики XVII столетия, получившие многие новые результаты, учились на трудах Архимеда.
На такой кажущейся теперь, по меньшей мере, сомнительной основе И. Кеплер (1571--1630) в своих сочинениях «Новая астрономия» (1609 г.) и «Стереометрия винных бочек» (1615 г.) правильно вычислил ряд площадей (например, площадь фигуры, ограниченной эллипсом) и объемов (тело разрезалось на бесконечно тонкие пластинки). Эти исследования были продолжены итальянскими математиками Б. Кавальери (1598--1647) и Э. Торричелли (1608--1647). Сохраняет свое значение и в наше время сформулированный Б. Кавальери принцип для площадей плоских фигур: Пусть прямые некоторого пучка параллельных пересекают фигуры Ф1 и Ф2 по отрезкам равной длины. Тогда площади фигур Ф1 и Ф2 равны.
Слайд 6
Методы математического анализа активно развивались в следующем столетии. В развитии интегрального
Строгое изложение теории интеграла появилось только в прошлом веке. Решение этой задачи связано с именами О. Коши, одного из крупнейших математиков немецкого ученого Б. Римана (1826--1866, см. рис. 4.), французского математика Г. Дарбу (1842-- 1917).
Слайд 72. Дифференциал в физике
Для вычисления дифференциала надо найти производную. Однако, помня
Слайд 8
Работа. Найдем работу, которую совершает заданная сила F при перемещении по отрезку оси х. Если сила F постоянна,
Заряд. Пусть q -- заряд, переносимый электрическим током через поперечное сечение проводника за время t. Если сила тока / постоянна, то за времяdt ток перенесет заряд, равный Idt. При силе тока, изменяющейся со временем по закону / = /(/), произведение I(t)dt дает главную часть приращения заряда на маленьком отрезке времени [/, t+-dt], т.е.- является дифференциалом заряда: dq = I{t)dt. Следовательно, сила тока является производной заряда по времени.
Масса тонкого стержня. Пусть имеется неоднородный тонкий стержень. Если ввести координаты так, как показано на рис. 130, то функция т= т(1) -- масса куска стержня от точки О до точки /. Неоднородность стержня означает, что его линейная плотность не является постоянной, а зависит от положения точки / по некоторому закону р = р(/). Если на маленьком отрезке стержня [/, / + d/] предположить, что плотность постоянна и равна р(/), то произведение p(/)d/ дает дифференциал массы dm. Значит, линейная плотность -- это производная массы по длине.
Теплота Рассмотрим процесс нагревания какого-нибудь вещества и вычислим количество теплоты Q{T), которое необходимо, чтобы нагреть 1 кг вещества от 0 °С до Т. Зависимость Q=Q(T) очень сложна и определяется экспериментально. Если бы теплоемкость с данного вещества не зависела от температуры, то произведение cdT дало бы изменение количества теплоты. Считая на малом отрезке [T, T+dT] теплоемкость постоянной, получаем дифференциал количества теплоты dQ = c(T)dT. Поэтому теплоемкость -- это производная теплоты по температуре.
Снова работа. Рассмотрим работу как функцию времени. Нам известна характеристика работы, определяющая ее скорость по времени, -- это мощность. При работе с постоянной мощностью N работа за время dt равна Ndt. Это выражение представляет дифференциал работы, т.е. dA = N(t)dt,и мощность выступает как производная работы по времени.
Слайд 93. Приложения определенного интеграла к решению некоторых задач механики и физики
1. Моменты и центры масс плоских кривых. Если дуга кривой задана уравнением y=f(x), a?x?b, и имеет плотность =(x), то статические моменты этой дуги Mx и My относительно координатных осей Ox и Oy равны
моменты инерции IХ и Iу относительно тех же осей Ох и Оу вычисляются по формулам
а координаты центра масс и -- по формулам
где l-- масса дуги, т. е.
Пример 1. Найти статические моменты и моменты инерции относительно осей Ох
и Оу дуги цепной линии y=chx при 0?x?1.
< Имеем: Следовательно,
В приложениях часто оказывается полезной следующая
Теорема Гульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.
Слайд 104. Дифференциальные уравнения
Многие физические законы имеют вид дифференциальных уравнений, т. е.
Слайд 11Пример
Уравнение механического движения. Пусть материальная точка массы т движется под действием силы F по оси х. Обозначим t время ее
Уравнение тх" = F называют уравнением, механического движения, где x = x(t)--неизвестная функция, т и F -- известные величины. В зависимости от условий задачи по-разному и записываются различные дифференциальные уравнения.
Слайд 125. Примеры решения задач в matlab
Задача 1. Построить семейство функций () и
Слайд 13
Программа:
x=-2:0.1:2;
title('{\itf(x)=x^{n}}');
xlabel('x');
ylabel('y');
hFigure=gcf;
set(hFigure,'Color',[1 1 1]);
hText=text;
set(hText,'FontSize',[18]);
for n=2:4
y=x.^n;
hold on
hPlot=plot(x,y);
set(hPlot,'Color',[1.8/n 0.7 0.5]);
set(hPlot,'LineWidth',2);
if n~=2
for i=1:length(y)
s='';
if y(i)==y1(i)
hold on
plot(x(i),y(i),'ko');
s=['('
hText=text(x(i),y(i)+2, s); set(hText,'FontSize',[16]);
end
end
end
y1=y; s2=['n=' num2str(n)];
hText=text(1.5, 1.5^2*n-1, s2); set(hText,'FontSize',[14]);
end
Слайд 15
Задача 2. Построить поверхность вращения графика функции заданной явно: (где ),
Слайд 16
Программа:
x1=0; x2=2; a=1;
u=x1:0.1:x2;
v=0:pi/20:2*pi;
[U,V]=meshgrid(u,v);
F=a*(exp(-U/a)+exp(U/a))/2;
X=U; Y=F.*cos(V); Z=F.*sin(V);
figure; hFigure=gcf;
set(hFigure,'Color',[0.9 0.8
surf(X,Y,Z)
colorbar;
view([-75,20])
hold on
x=0:0.1:x0; y=a*(exp(-x/a)+exp(x/a))/2;
hPlot=plot(x,y); set(hPlot,'LineWidth',5)
Слайд 17Список использованных источников
Ануфриев, И.Е. Самоучитель MatLab 5.3/6.х / И.Е. Ануфриев. -
Берман, Г.Н. Сборник задач по курсу математического анализа / Г.Н. Берман, И.Г. Араманович, А.Ф. Бермант и др. - М.: Наука, 1966. - 456 с.
Бермант, А.Ф. Краткий курс математического анализа для втузов / А.Ф. Бермант, И.Г. Араманович. - М.: Наука, 1966. - 736 с.
Гультяев, А. Визуальное моделирование в среде MatLab / А. Гультяев. - СПб.: Питер, 2001. - 553 с.
Демидович, Б.П. Задачи и упражнения по математическому анализу для втузов / Б.П. Демидович, Г.С. Бараненков, В.А. Ефименко и др. - М.: Наука, 1966. - 472 с.
Лазарев, Ю.Ф. MatLab 5.х / Ю.Ф. Лазарев. - Киев: BHV, 2000. - 388 с.
Мартынов, Н.Н. Matlab 5.х: вычисления, визуализация, программирование / Н.Н. Мартынов, А.П. Иванов. - М.: КУДИЦ-ОБРАЗ, 2000. - 336 с.
Куринной, Г.Ч. Математика: Справочник / Г.Ч. Куринной. - Харьков: Фолио; Ростов на Дону: Феникс, 1997. - 463 с.
Пискунов, Н.С. Дифференциальное и интегральное исчисление для втузов в 2 томах / Н.С. Пискунов. - М.: Наука, 1966. - 2 т. - 312 с.
Фихтенгольц, Г.М. Курс дифференциального и интегрального исчисления в 3 томах / Г.М. Фихтенгольц. - М.: Государственное изд-во физико-математической литературы, 1959. - т. 1-3.
Сайты http://www/informika.ru, htt://www.softline.ru, http://matlab.ru.












![интеграл Программа:x=-2:0.1:2;title('{\itf(x)=x^{n}}');xlabel('x');ylabel('y');hFigure=gcf;set(hFigure,'Color',[1 1 1]);hText=text;set(hText,'FontSize',[18]);for n=2:4y=x.^n;hold onhPlot=plot(x,y);set(hPlot,'Color',[1.8/n 0.7 0.5]);set(hPlot,'LineWidth',2);if n~=2for i=1:length(y)s='';if y(i)==y1(i)hold onplot(x(i),y(i),'ko');s=['(' Программа:x=-2:0.1:2;title('{\itf(x)=x^{n}}');xlabel('x');ylabel('y');hFigure=gcf;set(hFigure,'Color',[1 1 1]);hText=text;set(hText,'FontSize',[18]);for n=2:4y=x.^n;hold onhPlot=plot(x,y);set(hPlot,'Color',[1.8/n 0.7 0.5]);set(hPlot,'LineWidth',2);if n~=2for i=1:length(y)s='';if y(i)==y1(i)hold onplot(x(i),y(i),'ko');s=['(' num2str(x(i)) ',' num2str(y(i)) ')'];hText=text(x(i),y(i)+2, s); set(hText,'FontSize',[16]);endendendy1=y;](/img/thumbs/338dc4ad4941e1e934890a95f8cf9e02-800x.jpg)
![интеграл Программа:x1=0; x2=2; a=1;u=x1:0.1:x2; v=0:pi/20:2*pi; [U,V]=meshgrid(u,v); F=a*(exp(-U/a)+exp(U/a))/2; X=U; Y=F.*cos(V); Z=F.*sin(V);figure; hFigure=gcf;set(hFigure,'Color',[0.9 0.8 Программа:x1=0; x2=2; a=1;u=x1:0.1:x2; v=0:pi/20:2*pi; [U,V]=meshgrid(u,v); F=a*(exp(-U/a)+exp(U/a))/2; X=U; Y=F.*cos(V); Z=F.*sin(V);figure; hFigure=gcf;set(hFigure,'Color',[0.9 0.8 0.8]); surf(X,Y,Z)colorbar;view([-75,20]) hold on x=0:0.1:x0; y=a*(exp(-x/a)+exp(x/a))/2;](/img/thumbs/2546dbbcd57031529051ae41b6e47e77-800x.jpg)






