- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Дифференцированное обучение на уроках математики
Содержание
- 1. Дифференцированное обучение на уроках математики
- 2. Тема:Дифференцированное обучение на уроках математики
- 3. ПРОБЛЕМАКак учить всех результативно?Как готовить учащихся к успешной сдаче ОГЭ И ЕГЭ
- 4. Цели: 1)Найти индивидуальный подход к каждому ученику
- 5. Задачи:1)Развивать логическое , математическое мышление; 2) Развивать
- 6. Исследования психологовПоследние исследования психологов показали, что только
- 7. Основные положения теории поэтапного формирования умственных действий
- 8. Деление учащихся на 3 группыВзяв новый класс
- 9. Введение нового понятияТема.Квадрат суммы двух выражений. После
- 10. Технология закрепления новых понятийОстальные слушают и проговаривают
- 11. Приемы закрепления математических понятий1. В ходе
- 12. Отработку навыков провожу на уроках практикумах, где обучающиеся работают в группах, в парах(могут консультировать друг друга).
- 13. Принцип непрерывного повторенияУсвоение того или иного понятия
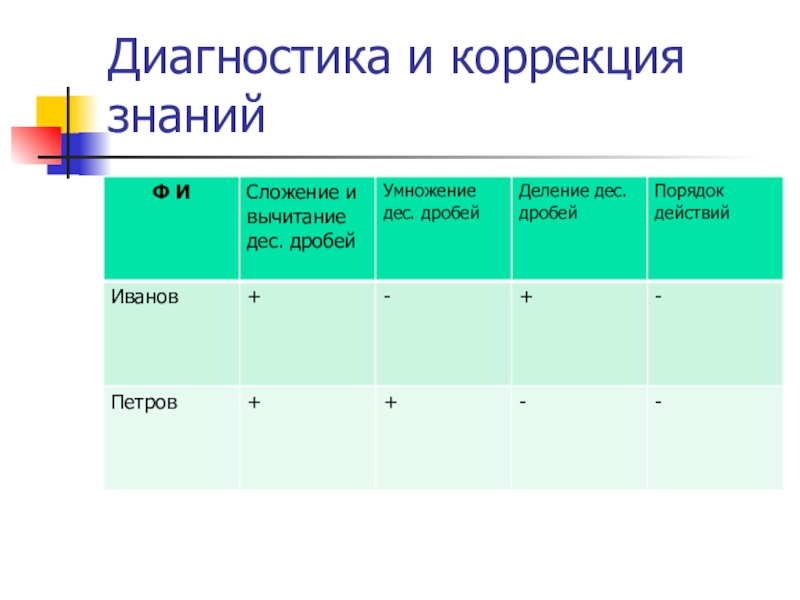
- 14. Диагностика и коррекция знаний
- 15. Решение трудных и многошаговых задач1.Разбиваю задачу на
- 16. Обучающие самостоятельные работы Обучающая самостоятельная работа для
- 17. Тренировочные карточки с образцами решенияУчащимся, которые
- 18. Три уровня в самостоятельной работеВ любой контрольной
- 19. Домашнее заданиеДомашнее задание учащиеся получают дифференцированное:1. задания
- 20. Развитие речи :1)Письменное решение задач рассматриваю как
- 21. Соблюдение принципа здоровьесбережения. Данная методика позволяет формировать
- 22. ДИАГНОСТИКА ПСИХОЛОГА ОТДЕЛЬНЫХ УЧАЩИХСЯ
- 23. Вывод: Наблюдается рост интеллектуального развития всех представленных
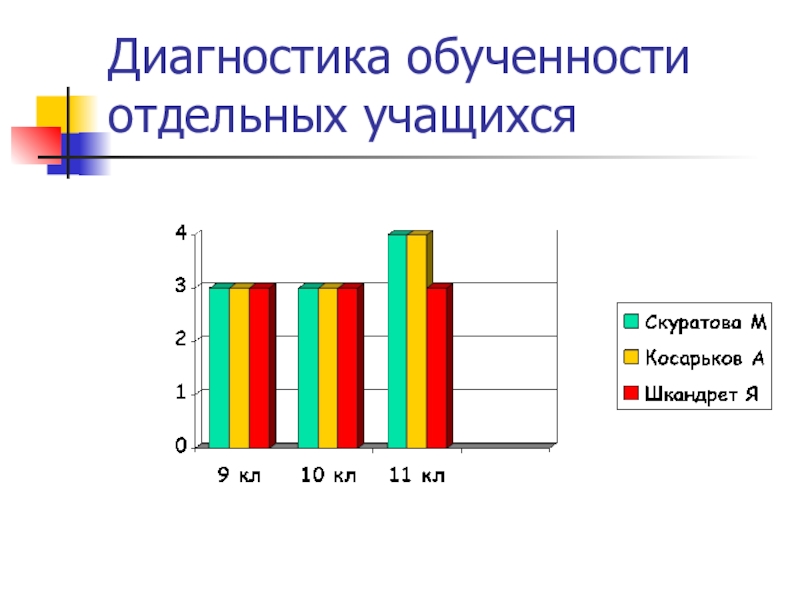
- 24. Диагностика обученности отдельных учащихся
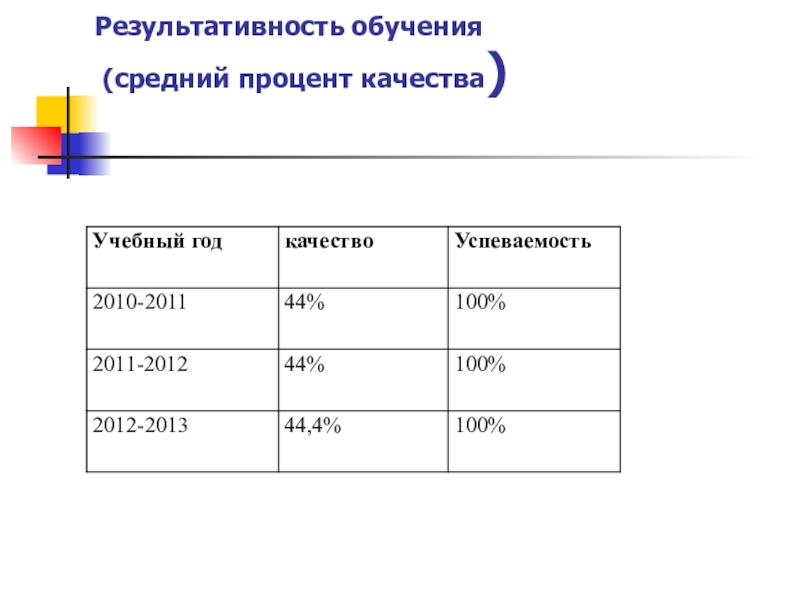
- 25. Результативность обучения (средний процент качества)
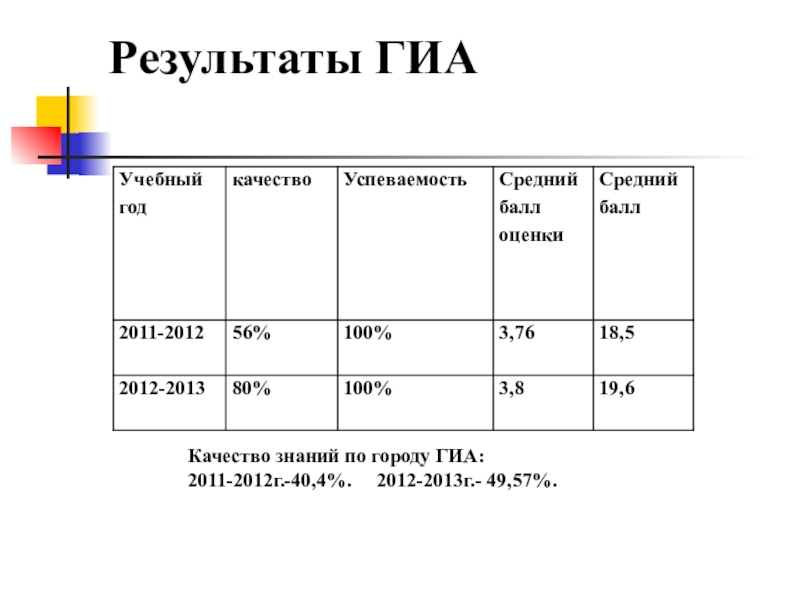
- 26. Результаты ГИА Качество знаний по городу ГИА: 2011-2012г.-40,4%. 2012-2013г.- 49,57%.
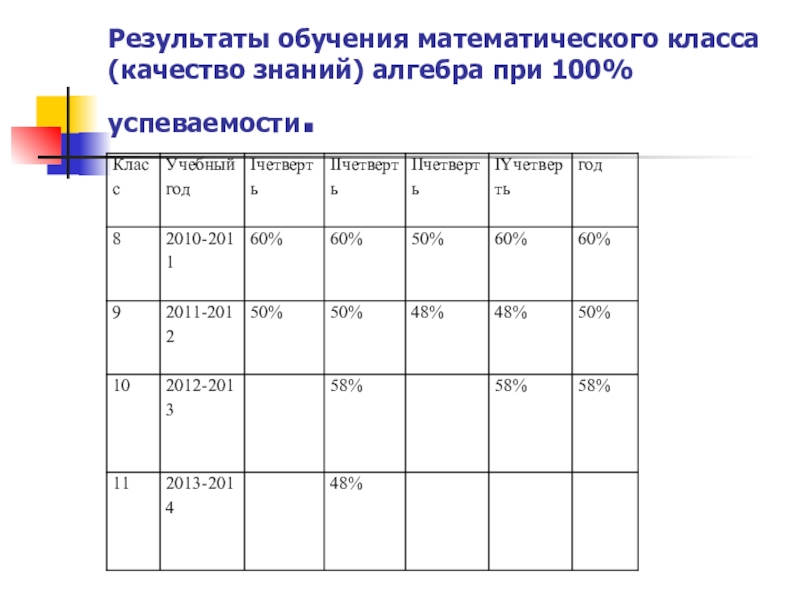
- 27. Результаты обучения математического класса (качество знаний) алгебра при 100% успеваемости.
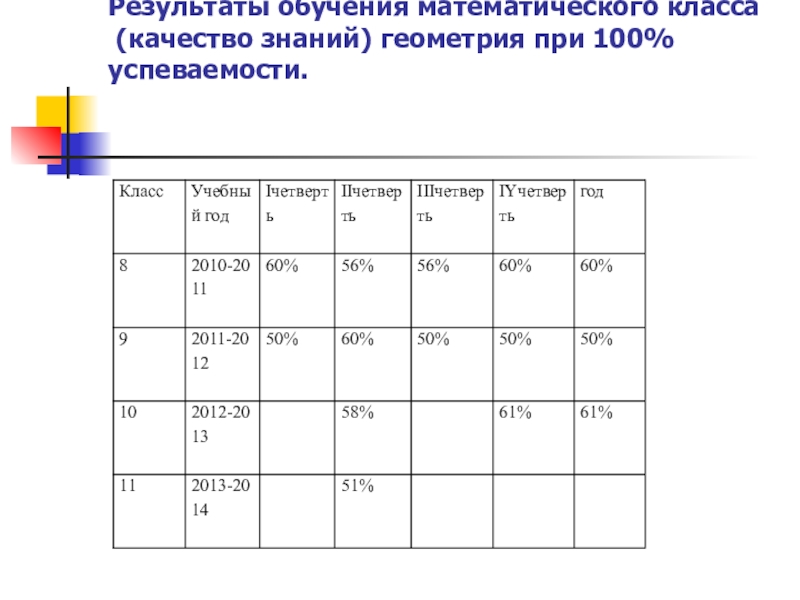
- 28. Результаты обучения математического класса (качество знаний) геометрия при 100% успеваемости.
- 29. Работа с одаренными учащимся. В 5 –
- 30. Вывод: Основа моей методики – признание индивидуальности
Тема:Дифференцированное обучение на уроках математики
Слайд 1Моу лицей №6 г Северобайкальск
Коляда Наталья Ивановна
Учитель математики
Высшей категории
Опытно – экспериментальная методическая разработка
Слайд 4Цели:
1)Найти индивидуальный подход к каждому ученику с целью его максимального
развития.
2)Готовить всех учащихся к успешной сдаче ЕГЭ и ГИА.
3)Достижение всеми учащимися математической подготовки на уровне ГОСУДАРСТВЕНОГО СТАНДАРТА ОБРАЗОВАНИЯ.
2)Готовить всех учащихся к успешной сдаче ЕГЭ и ГИА.
3)Достижение всеми учащимися математической подготовки на уровне ГОСУДАРСТВЕНОГО СТАНДАРТА ОБРАЗОВАНИЯ.
Слайд 5Задачи:
1)Развивать логическое , математическое мышление;
2) Развивать гибкость мышления;
3) Учить учащихся
работать в коллективе.
4)Создавать комфортный темп работы обучаемого
5)Научить учащихся определять свои возможности.
6)Выработать прочные умения и навыки на уровне Государственного Стандарта Образования.
4)Создавать комфортный темп работы обучаемого
5)Научить учащихся определять свои возможности.
6)Выработать прочные умения и навыки на уровне Государственного Стандарта Образования.
Слайд 6Исследования психологов
Последние исследования психологов показали, что только 9,4% обучающихся имеют выраженное
словестно-логическое мышление. Самая большая часть учащихся и самая неуспешная в учении имеет наглядно-образное мышление; примерно 52%.
Слайд 7Основные положения теории поэтапного формирования умственных действий
1) Создание мотивации обучаемого.Этап
предварительного ознакомления с целью действия.
2)Составление схемы ориентировочной основы действий.(памятки, алгоритмы, образцы и т.д.)
3)Проговаривания усваиваемого действия вслух
(проговаривание вслух правила, алгоритма, хоровое решение задач и т. д),глядя на опору, в учебник или образец.
4)Проговаривание вслух без опоры.(На этом этапе учащиеся проговаривают словами все операции в развернутом виде без каких либо пропусков)
5)Действие сопровождается проговариванием про себя.
6)Действие в умственном плане.
2)Составление схемы ориентировочной основы действий.(памятки, алгоритмы, образцы и т.д.)
3)Проговаривания усваиваемого действия вслух
(проговаривание вслух правила, алгоритма, хоровое решение задач и т. д),глядя на опору, в учебник или образец.
4)Проговаривание вслух без опоры.(На этом этапе учащиеся проговаривают словами все операции в развернутом виде без каких либо пропусков)
5)Действие сопровождается проговариванием про себя.
6)Действие в умственном плане.
Слайд 8Деление учащихся на 3 группы
Взяв новый класс провожу тестирование(выясняю уровень умений
и навыков),а также прошу психолога провести диагностику уровня интеллектуального развития.
Затем учащихся делю на 3 группы:
1) Группа – учащиеся, которым достаточно 1 раз прослушать и 1-2 раза проговорить и решить самостоятельно 1 – 2 типовые задачи. Далее им даю более сложные, творческие задания.
2) Группа – учащиеся которым необходимо прослушать и проговорить 2 – 3 раза и самостоятельно решить 3 – 4 типовые задачи; Далее они получают задания в 2 – 3 шага.
3) Группа – учащиеся, которые должны прослушать и проговорить 4 – 5 раз и решить самостоятельно до 10 типовых задач, тогда правило , теорема ,понятие будут усвоены на всю жизнь.
Затем учащихся делю на 3 группы:
1) Группа – учащиеся, которым достаточно 1 раз прослушать и 1-2 раза проговорить и решить самостоятельно 1 – 2 типовые задачи. Далее им даю более сложные, творческие задания.
2) Группа – учащиеся которым необходимо прослушать и проговорить 2 – 3 раза и самостоятельно решить 3 – 4 типовые задачи; Далее они получают задания в 2 – 3 шага.
3) Группа – учащиеся, которые должны прослушать и проговорить 4 – 5 раз и решить самостоятельно до 10 типовых задач, тогда правило , теорема ,понятие будут усвоены на всю жизнь.
Слайд 9Введение нового понятия
Тема.Квадрат суммы двух выражений.
После введения правила, мы его
черточками делим на смысловые части.
Квадрат суммы двух выражений // равен квадрату первого выражения// плюс удвоенное произведение первого на второе // плюс квадрат второго выражения.
Выполняя задание читаем смысловые части правила:1) убеждаемся, что это квадрат суммы двух выражений 2)находим квадрат первого выражения 3) находим удвоенное произведение первого выражения на второе 4) находим квадрат второго выражения.
Проговаривая каждое действие вслух, читая правило.
После того как правило выучено, выполняя действие проговариваем правило.
После выработки навыка проводим действие в умственном плане.
Квадрат суммы двух выражений // равен квадрату первого выражения// плюс удвоенное произведение первого на второе // плюс квадрат второго выражения.
Выполняя задание читаем смысловые части правила:1) убеждаемся, что это квадрат суммы двух выражений 2)находим квадрат первого выражения 3) находим удвоенное произведение первого выражения на второе 4) находим квадрат второго выражения.
Проговаривая каждое действие вслух, читая правило.
После того как правило выучено, выполняя действие проговариваем правило.
После выработки навыка проводим действие в умственном плане.
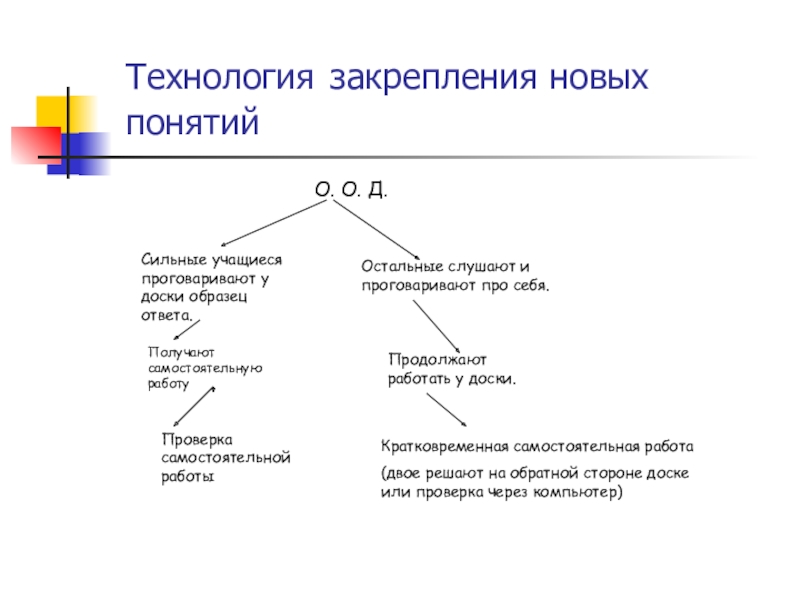
Слайд 10Технология закрепления новых понятий
Остальные слушают и проговаривают про себя.
О. О. Д.
Сильные
учащиеся проговаривают у доски образец ответа.
Получают самостоятельную работу
Продолжают работать у доски.
Проверка самостоятельной работы
Кратковременная самостоятельная работа
(двое решают на обратной стороне доске или проверка через компьютер)
Слайд 11 Приемы закрепления математических понятий
1. В ходе решения математических задач упражнений
учащиеся обосновывают каждый шаг, формулируют по ходу решения правила, теоремы, определения.
2.Во время фронтального опроса учащиеся должны привести пример и контрпример. (y=cosx периодическая, y=cosx+x не периодическая)
3Для более прочного запоминания повторяем 2-3 раза, но каждый раз с новыми примерами
4. При таком воспроизведении слабоуспевающий ученик прослушав своего товарища дает четкий и ясный ответ.
2.Во время фронтального опроса учащиеся должны привести пример и контрпример. (y=cosx периодическая, y=cosx+x не периодическая)
3Для более прочного запоминания повторяем 2-3 раза, но каждый раз с новыми примерами
4. При таком воспроизведении слабоуспевающий ученик прослушав своего товарища дает четкий и ясный ответ.
Слайд 12
Отработку навыков провожу на уроках практикумах, где обучающиеся работают в группах,
в парах(могут консультировать друг друга).
Слайд 13Принцип непрерывного повторения
Усвоение того или иного понятия не всегда укладывается в
рамки времени, отведенное программой; поэтому в своей работе использую принцип непрерывного повторения.
Как планировать повторение?
Как планировать повторение?
Слайд 15Решение трудных и многошаговых задач
1.Разбиваю задачу на отдельные элементарные задания, которые
разбираем либо в устных упражнениях либо решаем отдельно.
2.Предлагаю решить в группах. .
3. Затем разбираем решение на доске. Такой метод позволяет решить задачу не только сильным учащимся.
2.Предлагаю решить в группах. .
3. Затем разбираем решение на доске. Такой метод позволяет решить задачу не только сильным учащимся.
Слайд 16Обучающие самостоятельные работы
Обучающая самостоятельная работа для каждой группы учащихся своя.
Тема. Деление на десятичную дробь и натуральное число:
Тема: Деление на натуральное число, на десятичную дробь.
1.Вариант:1) 15,3:3 2)8,4:4 3)0,3:4 4)0,6:8 5)2,18:10 6)4,3:100 7)1,976:1,9
8)7,82:1,7 9)29,67:7,6 !0)8:64 11)36,4:0,065 12)(1,72+17,48):0,6 13)4:0,8 – 0,05
2.Вариант: 1)(28,5:19)1,4 2)2,4(40,6:29) 3)(7,81 – 3,97):0,4 4)50 – 23(66,6:37)
5)(41 – 38,7)8,8 + 4:0,8 6)(51 -48,8)7,7 +6:0,75
3.Вариант: 1)102 –(155,4:14,8 + 2,1)3,5
2)871,017:5,05 – 11,376 3) 508,3 + 891:35,4 -11,376
4)0,125:0,25 +(36 -34,4)3,2 5)(953,54 – 396,41):75 8 +4,12:0,4
Тема: Деление на натуральное число, на десятичную дробь.
1.Вариант:1) 15,3:3 2)8,4:4 3)0,3:4 4)0,6:8 5)2,18:10 6)4,3:100 7)1,976:1,9
8)7,82:1,7 9)29,67:7,6 !0)8:64 11)36,4:0,065 12)(1,72+17,48):0,6 13)4:0,8 – 0,05
2.Вариант: 1)(28,5:19)1,4 2)2,4(40,6:29) 3)(7,81 – 3,97):0,4 4)50 – 23(66,6:37)
5)(41 – 38,7)8,8 + 4:0,8 6)(51 -48,8)7,7 +6:0,75
3.Вариант: 1)102 –(155,4:14,8 + 2,1)3,5
2)871,017:5,05 – 11,376 3) 508,3 + 891:35,4 -11,376
4)0,125:0,25 +(36 -34,4)3,2 5)(953,54 – 396,41):75 8 +4,12:0,4
Слайд 17 Тренировочные карточки с образцами решения
Учащимся, которые долго усваивают программный материал.
Или пропустили занятия, предлагаю тренировочные карточки с образцами решения типовых задач:
Тема: Решение линейных уравнений
Пример. Решите уравнение 2(0,4х – 3) = 2.
Решение: 0,8х – 6 = 2, 0,8х = 2 + 6, 0,8х = 8, х = 8:0,8,
Х = 10. Ответ: х = 10.
Задание. Решите уравнение: а)0,1(х + 2) = 0,7.
б) 0,5(3х – 5) = 3
Тема: Решение линейных уравнений
Пример. Решите уравнение 2(0,4х – 3) = 2.
Решение: 0,8х – 6 = 2, 0,8х = 2 + 6, 0,8х = 8, х = 8:0,8,
Х = 10. Ответ: х = 10.
Задание. Решите уравнение: а)0,1(х + 2) = 0,7.
б) 0,5(3х – 5) = 3
Слайд 18Три уровня в самостоятельной работе
В любой контрольной и самостоятельной работе должно
быть 3 уровня:
1.уровень – задания, соответствуют стандарту образования(обычно 3)
2.Уровень-задания допускают 2-3 шага.
Применение знаний в стандартной обстановке.
3.Уровень – применение знаний в новой обстановке (при не привычных сочетаниях данных).
Контрольную работу учащиеся выполняют под копирку и лучше давать не на весь урок, а так чтобы анализ контрольной работы провести сразу, пока учащиеся не потеряли к ней интерес. У учащихся остаются копии решений .
1.уровень – задания, соответствуют стандарту образования(обычно 3)
2.Уровень-задания допускают 2-3 шага.
Применение знаний в стандартной обстановке.
3.Уровень – применение знаний в новой обстановке (при не привычных сочетаниях данных).
Контрольную работу учащиеся выполняют под копирку и лучше давать не на весь урок, а так чтобы анализ контрольной работы провести сразу, пока учащиеся не потеряли к ней интерес. У учащихся остаются копии решений .
Слайд 19Домашнее задание
Домашнее задание учащиеся получают дифференцированное:
1. задания на отработку навыков (аналогичные
тем, которые выполняли в классе)
2.Задачи повышенной сложности, требующие применить знания в новой непривычной ситуации.
Учащиеся сами выбирают сложность задания сами.
2.Задачи повышенной сложности, требующие применить знания в новой непривычной ситуации.
Учащиеся сами выбирают сложность задания сами.
Слайд 20Развитие речи :
1)Письменное решение задач рассматриваю как миниатюрное сочинение.
2)Учащиеся должны овладеть
терминологией- это необходимое условие развития речи.
3)Увеличиваю время разговорной речи учащихся, т.е. требую от них связанного рассказа без наводящих вопросов.
Все выше сказанное способствует усвоению новых понятий, правил, теорем, приучает учащихся к правильной, ясной, убедительной, четкой и краткой, но одновременно насыщенной смыслом речи.
3)Увеличиваю время разговорной речи учащихся, т.е. требую от них связанного рассказа без наводящих вопросов.
Все выше сказанное способствует усвоению новых понятий, правил, теорем, приучает учащихся к правильной, ясной, убедительной, четкой и краткой, но одновременно насыщенной смыслом речи.
Слайд 21Соблюдение принципа здоровьесбережения.
Данная методика позволяет формировать новые действия легче ,
без зазубривания нового материала, так как он усваивается в процессе деятельности.
При отработке навыков работа для каждого посильна и каждый выбирает
Сложность себе сам .
Помимо этого провожу физкультминутки , гимнастику для глаз, для пальцев, самомассаж биологически активных точек.
При отработке навыков работа для каждого посильна и каждый выбирает
Сложность себе сам .
Помимо этого провожу физкультминутки , гимнастику для глаз, для пальцев, самомассаж биологически активных точек.
Слайд 23Вывод:
Наблюдается рост интеллектуального развития всех представленных в диаграмме учащихся. Среди
представленных познавательных процессов (память, внимание, мышление, воображение) возрос уровень памяти у Косарькова. Уровень логического мышления возрос у всех трех учащихся, что говорит о том, что дополнительные занятия по математике значительно отразились на росте логического мышления и общего уровня интеллектуального развития.
Слайд 28Результаты обучения математического класса
(качество знаний) геометрия при 100% успеваемости.
Слайд 29Работа с одаренными учащимся.
В 5 – 7 классах веду элективный
курс «Решение текстовых задач»
2010 г – моя ученица Белогуб Кристина на конференции «шаг в будущее» получила диплом 2-й степени за работу «Прямоугольный треугольник»
2012г –Гаськова Настя на конференции «шаг в будущее» получила диплом III степени за работу « Квадратные уравнения»
2013г- Ануфрейчук Настя на конференции «шаг в будущее» получила диплом III степени за работу «Сечения многогранников».
На городских олимпиадах по математике мои учащиеся занимают призовые места:
2011-2012 уч.год – Гаськова Настя - II место.
2013-2014 уч.год - Гаськова Настя - I место ( рекомендована на республику).
2013-2014 уч.год – Данилова Тоня -II место.
2010 г – моя ученица Белогуб Кристина на конференции «шаг в будущее» получила диплом 2-й степени за работу «Прямоугольный треугольник»
2012г –Гаськова Настя на конференции «шаг в будущее» получила диплом III степени за работу « Квадратные уравнения»
2013г- Ануфрейчук Настя на конференции «шаг в будущее» получила диплом III степени за работу «Сечения многогранников».
На городских олимпиадах по математике мои учащиеся занимают призовые места:
2011-2012 уч.год – Гаськова Настя - II место.
2013-2014 уч.год - Гаськова Настя - I место ( рекомендована на республику).
2013-2014 уч.год – Данилова Тоня -II место.
Слайд 30Вывод:
Основа моей методики – признание индивидуальности ученика, создание условий для
его всестороннего развития.
данная методика, в условиях лицея в небольшом городе, где класс с углубленным изучением математики создается из 2-3 классов, дает неплохие результаты. Ее можно использовать и в общеобразовательной школе.
данная методика, в условиях лицея в небольшом городе, где класс с углубленным изучением математики создается из 2-3 классов, дает неплохие результаты. Ее можно использовать и в общеобразовательной школе.