- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Делимость чисел
Содержание
- 1. Делимость чисел
- 2. Натуральные числа, на которые делится данное число
- 3. 1236918275454108162216…Натуральное число, которое делится на другое натуральное
- 4. Натуральное число, имеющее ровно два делителя, называется
- 5. Так как греки делали записи на покрытых
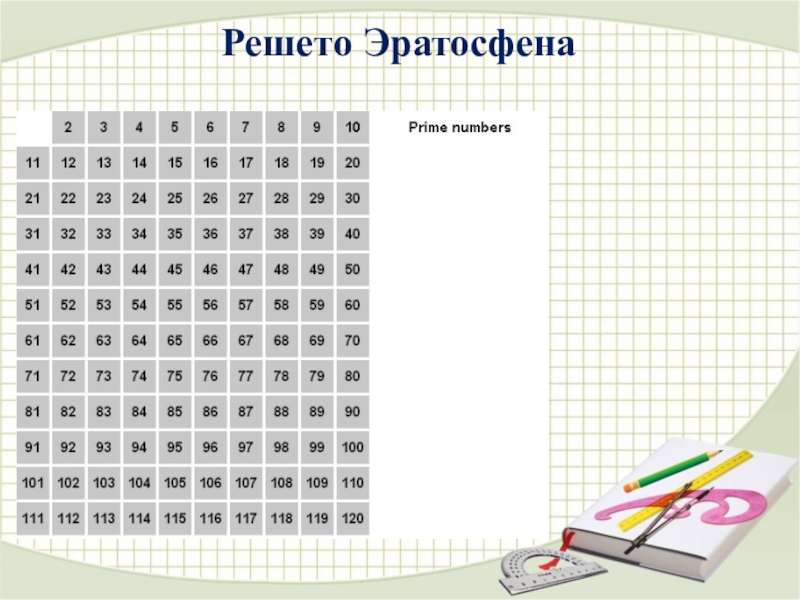
- 6. Решето Эратосфена
- 7. Признаки делимости
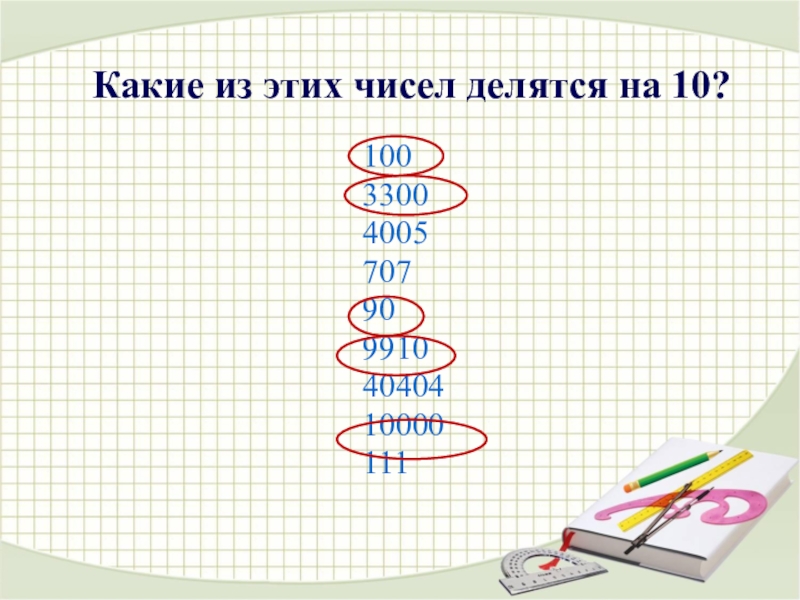
- 8. Какие из этих чисел делятся на 10?100330040057079099104040410000111
- 9. Какие из этих чисел делятся на 5?10035554006707909913404051000011111
- 10. 4014; 40138; 3528; 8507; 93274014; 40138; 3528;
- 11. 1010; 3555; 40108; 7307; 9271010; 3555; 40108;
- 12. Разложение числа на простые множителиЛюбое составное число
- 13. Разложение на простые множители330×××103311352330 = 2 ∙
- 14. Разложение на простые множителиВсякое составное число можно
- 15. Разложение на простые множители126026302315310533557711260 = 2 ∙
- 16. Наибольший общий делитель (НОД)Среди запасов белки на
- 17. 2Алгоритм нахождения НОД126026302315310533557713400170028502425585517171НОД(1260; 3400) = 2∙2∙5 =
- 18. Делители 42:1; 2; 3; 6; 7; 14;
- 19. Женя проезжает круговую дистанцию на мотоцикле за
- 20. НОК(12; 15; 20; 60) = 60Если одно
- 21. 275325555160302153551Алгоритм нахождения НОКАлгоритм вычисления НОК: Найти НОК(
- 22. Деление с остаткомВ том случае, если одно
- 23. Какое число называется делителем натурального числа?Какое число
- 24. Что такое делитель натурального числа? Найти все
- 25. Найти НОД(425; 170). Найти НОК(300; 170).Какие числа
- 26. Ответы к заданиям по теме «Делимость»
- 27. После изучения темы и разбора основных вопросов выполни тест-http://onlinetestpad.com/t/4d0b88dca4454608a4813e4f3ea45c26 «Делимость чисел»
Слайд 2Натуральные числа, на которые делится данное число без остатка, называются его
Делители
Число 1 является делителем любого натурального числа.
Любое натуральное число имеет ограниченное число делителей.
Делители числа 36 – это 1, 2, 3, 4, 6, 9, 12, 18, 36
Слайд 31
2
3
6
9
18
27
54
54
108
162
216
…
Натуральное число, которое делится на другое натуральное число без остатка, называют
Натуральные числа, на которые делится данное число без остатка, называются его делителями.
Делители. Кратные
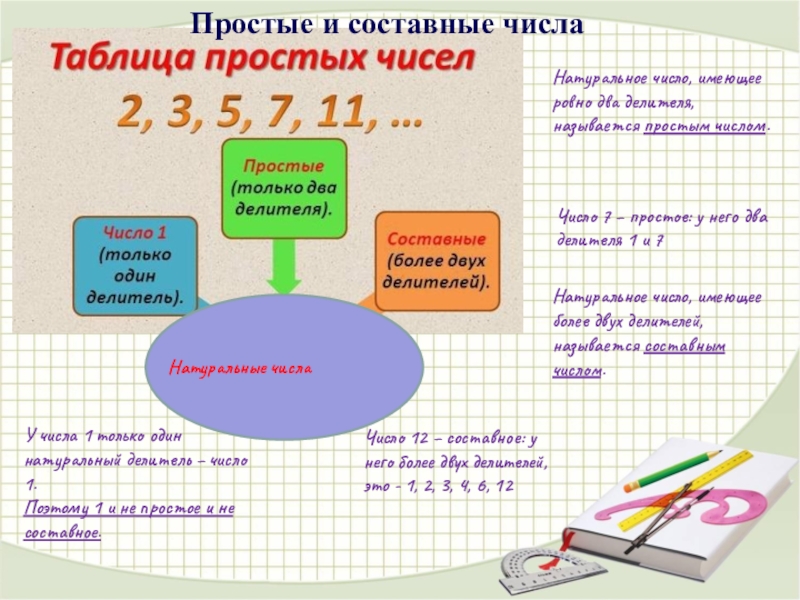
Слайд 4Натуральное число, имеющее ровно два делителя, называется простым числом.
Натуральное число,
У числа 1 только один натуральный делитель – число 1.
Поэтому 1 и не простое и не составное.
Число 7 – простое: у него два делителя 1 и 7
Число 12 – составное: у него более двух делителей, это - 1, 2, 3, 4, 6, 12
Простые и составные числа
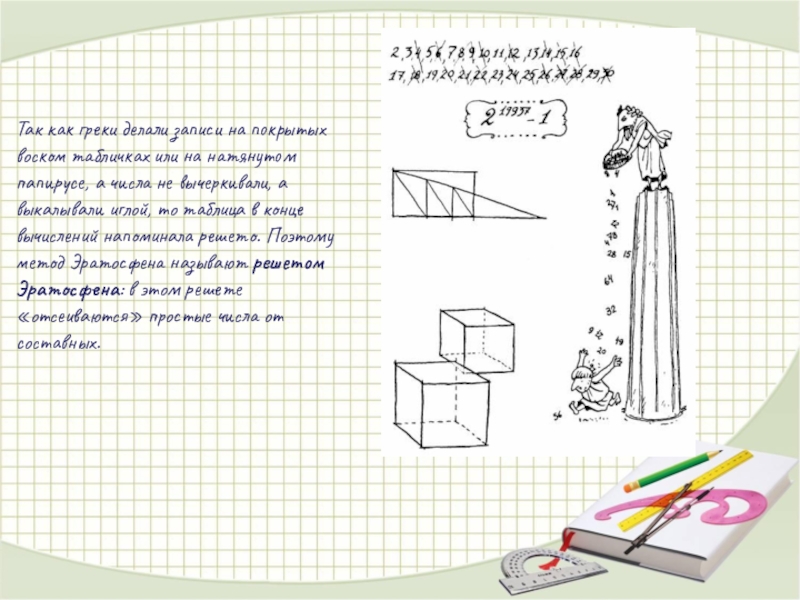
Слайд 5Так как греки делали записи на покрытых воском табличках или на
Слайд 104014; 40138; 3528; 8507; 9327
4014; 40138; 3528; 8507; 9327
Признак делимости на
Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3.
4+0+1+4=9 – делится на 3
3+5+2+8=18 – делится на 3
4+0+1+3+8=16 – не делится на 3
8+5+0+7=20 – не делится на 3
9+3+2+7=21 – делится на 3
Слайд 111010; 3555; 40108; 7307; 927
1010; 3555; 40108; 7307; 927
Признак делимости на
Если сумма цифр числа делится на 9, то и число делится на 9; если сумма цифр числа не делится на 9, то и число не делится на 9.
1+0+1+0=2 – не делится на 9
3+5+5+5=18 – делится на 9
4+0+1+0+8=13 – не делится на 9
7+3+0+7=17 – не делится на 9
9+2+7=18 – делится на 9
Слайд 12Разложение числа на простые множители
Любое составное число может быть представлено в
92820=2∙2∙3∙5∙7∙13∙17
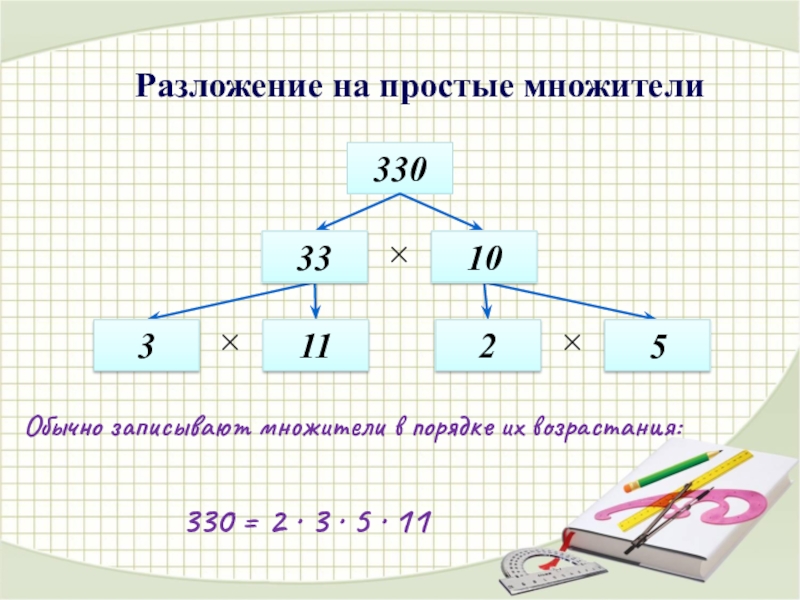
Слайд 13Разложение на простые множители
330
×
×
×
10
33
11
3
5
2
330 = 2 ∙ 3 ∙ 5 ∙
Обычно записывают множители в порядке их возрастания:
Слайд 14Разложение на простые множители
Всякое составное число можно разложить на простые множители.
2) При любом способе получается одно и то же разложение, если не учитывать порядка записи множителей.
3) При разложении чисел на простые множители используют признаки делимости.
Слайд 15Разложение на простые множители
1260
2
630
2
315
3
105
3
35
5
7
7
1
1260 = 2 ∙ 2 ∙ 3 ∙
3400
2
1700
850
2
425
5
85
5
17
17
1
2
3400 = 2 ∙ 2 ∙ 2 ∙ 5 ∙ 5 ∙ 17
Слайд 16Наибольший общий делитель (НОД)
Среди запасов белки на зиму имеется 45 орехов
Делители 45:
1; 3; 5; 9; 15; 45
Делители 60:
1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60
Общие делители:
1; 3; 5; 15
15 − наибольший общий делитель
Слайд 172
Алгоритм нахождения НОД
1260
2
630
2
315
3
105
3
35
5
7
7
1
3400
1700
2
850
2
425
5
85
5
17
17
1
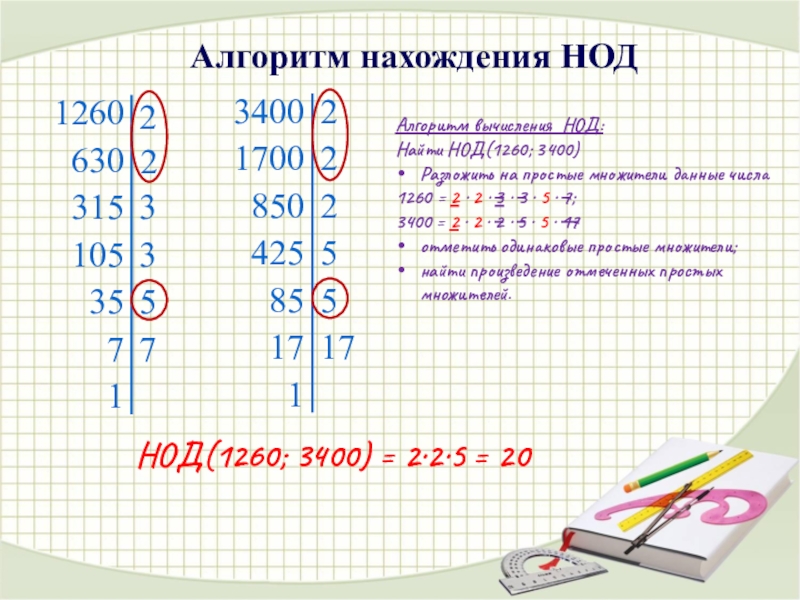
НОД(1260; 3400) = 2∙2∙5 = 20
Алгоритм вычисления НОД:
Найти
Разложить на простые множители данные числа
1260 = 2 · 2 · 3 · 3 ∙ 5 ∙ 7;
3400 = 2 · 2 · 2 · 5 ∙ 5 ∙ 17
отметить одинаковые простые множители;
найти произведение отмеченных простых множителей.
Слайд 18Делители 42:
1; 2; 3; 6; 7; 14; 21; 42
Делители 55:
1; 5;
Общие делители:
1
- НОД(55; 42)
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Одинаковых простых множителей у рассматриваемых чисел может и не быть.
Например: 12 = 2 · 2 · 3; 55 = 5 · 11.
Значит НОД(12; 55) = 1.
Такие числа называются взаимно простыми.
НОД
Слайд 19Женя проезжает круговую дистанцию на мотоцикле за 75 секунд, а Валя
Кратные 60:
60; 120; 180; 240; 300; 360; 420; 480; 540; 600; …
Кратные 75:
75; 150; 225; 300; 375; 450; 525; 600; …
Общие кратные:
300; 600; 900; 1200; …
− наименьшее общее кратное
Наименьшее общее кратное (НОК)
Слайд 20НОК(12; 15; 20; 60) = 60
Если одно из данных чисел делится
Кратные 15:
15; 30; 45; 60; 75; 90; 105; …
Кратные 12:
12; 24; 36; 48; 60; 72; …
Кратные 20:
20; 40; 60; 80; 100; 120; 140; …
Кратные 60:
60; 120; 180; 240; 300; 360; …
НОК
Если НОД( а; b) = 1, то НОК( а; b) = а · b.
Также, НОК( а; b) · НОД( а; b) = а · b.
Слайд 212
75
3
25
5
5
5
1
60
30
2
15
3
5
5
1
Алгоритм нахождения НОК
Алгоритм вычисления НОК:
Найти НОК( 75; 60)
Разложить на простые
75 = 3 · 5 · 5;
60 = 2 · 2 · 3 · 5
отметить одинаковые простые множители;
записать произведение всех простых множителей одного из чисел и всех неотмеченных множителей второго числа.
НОК( 75; 60) = 3 · 5 · 5 ∙ 2 ∙ 2 = 300
Слайд 22Деление с остатком
В том случае, если одно натуральное число не делится
Пусть, например, нужно разделить 325 на 4.
Действие записывают так: 325 : 4 = 81 (1 остаток).
Окончательный результат деления с остатком числа 325 на 4 записывается так: 325 = 4 · 81 + 1
Делимое = Делитель ⋅ Неполное Частное + Остаток
Слайд 23Какое число называется делителем натурального числа?
Какое число называется кратным натурального числа?
Признаки
Какие натуральные числа называются простыми? составными?
Алгоритм разложения натуральных чисел на простые множители.
Алгоритм вычисления НОД.
Какие натуральные числа называются взаимно простыми?
Алгоритм вычисления НОК.
Деление натуральных чисел с остатком.
Вопросы по теме «Делимость чисел»
Слайд 24Что такое делитель натурального числа? Найти все делители числа 48.
Перечислить основные
Что такое кратное натурального числа? Найти три кратных для числа 13.
Какие числа называются простыми? составными? Какое число не является ни простым, ни составным? Разложить на простые множители число 9999.
Задания по теме «Делимость»
Слайд 25Найти НОД(425; 170). Найти НОК(300; 170).
Какие числа называются взаимно простыми? Привести
Объяснить, что такое деление с остатком? Выполнить деление с остатком 759 : 4 . Записать окончательный результат вычисления.
Задания по теме «Делимость»
Слайд 27После изучения темы и разбора основных вопросов выполни тест-http://onlinetestpad.com/t/4d0b88dca4454608a4813e4f3ea45c26 «Делимость чисел»
