- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Задачки для 5-7 классов
Содержание
- 1. Задачки для 5-7 классов
- 2. Табличный способ решения логических задачОбъекты двух
- 3. Однажды в Артеке за круглым столом оказалось
- 4. Слайд 4
- 5. Однажды в Артеке за круглым столом оказалось
- 6. ––
- 7. Однажды в Артеке за круглым столом оказалось
- 8. –––––––+–––––+–––+––+–+
- 9. Ответ: Юра живёт в Новгороде,
- 10. Три подружкиТри подружки, Аня, Света и Настя,
- 11. Заполняем таблицуВ белом стаканчике – не банановый коктейль. В голубой стаканчик налит ванильный коктейль.
- 12. Заполняем таблицуАне достался не белый стаканчик, а
- 13. Решение задач с помощью графовЛюбитель скейтборда.Сергей -
- 14. Цены в магазине «Спорт»
- 15. Вопросы Сколько различных скейтбордов может собрать Сергей
- 16. Для скейтборда можно выбрать одну
- 17. К любой из платформ можно выбрать
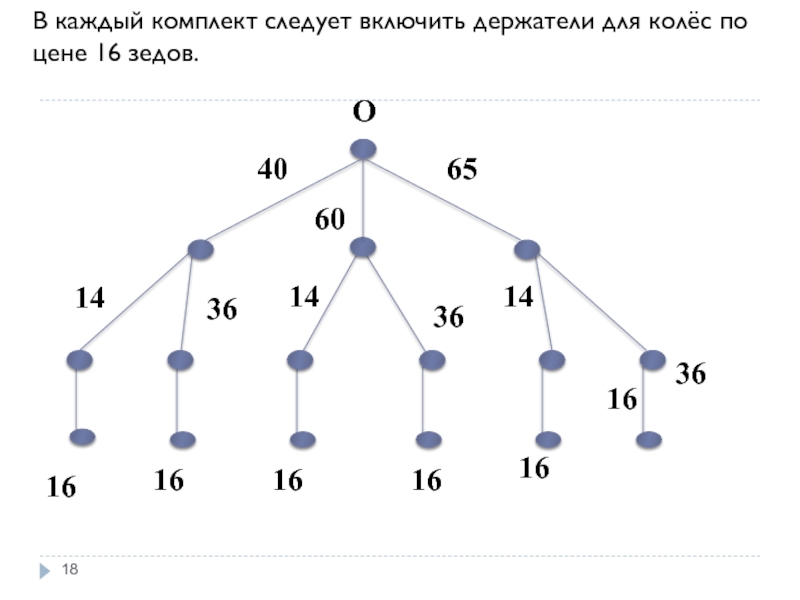
- 18. В каждый комплект следует включить держатели для колёс по цене 16 зедов.
- 19. В каждый комплект следует включить
- 20. Анализ полученных результатовВсего можно собрать 12 различных
- 21. Использование схем состава. Посылка от бабушки
- 22. Бабушка прислала Ивану посылку с яблоками и
- 23. Слайд 23
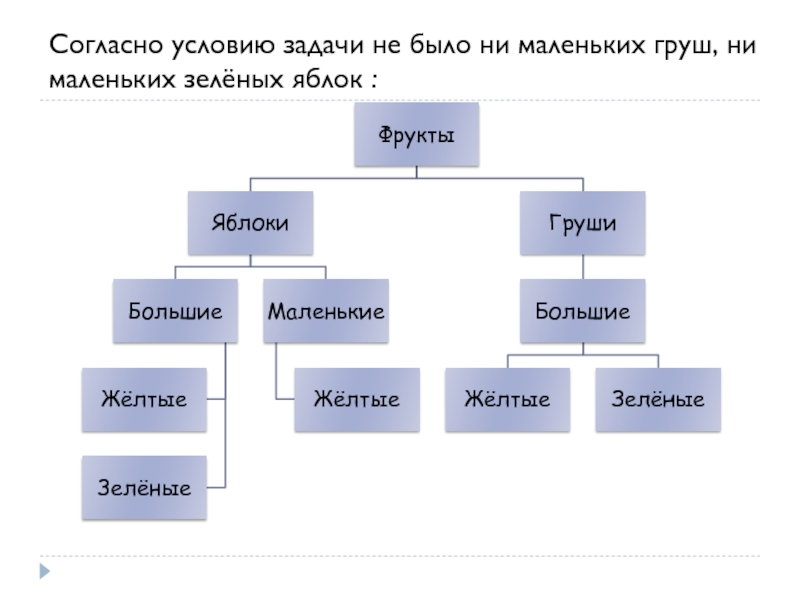
- 24. Согласно условию задачи не было ни маленьких груш, ни маленьких зелёных яблок :
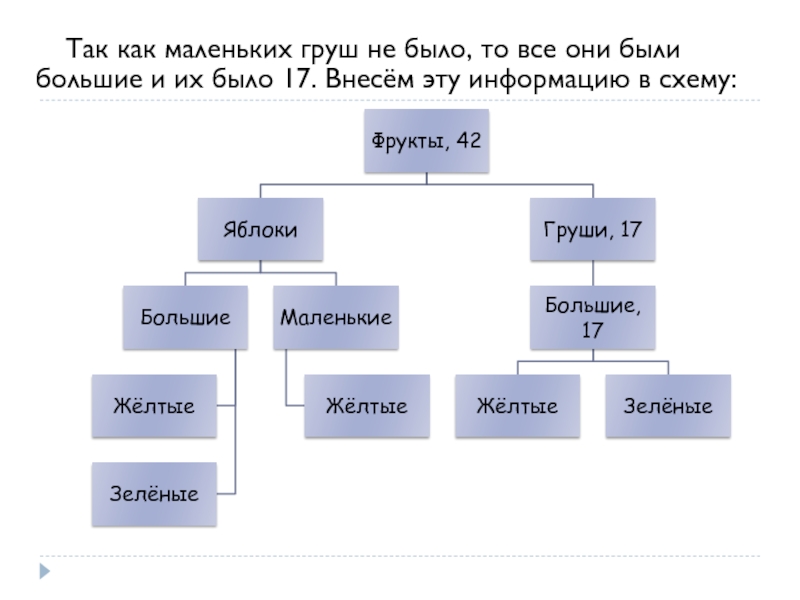
- 25. Так как маленьких груш не
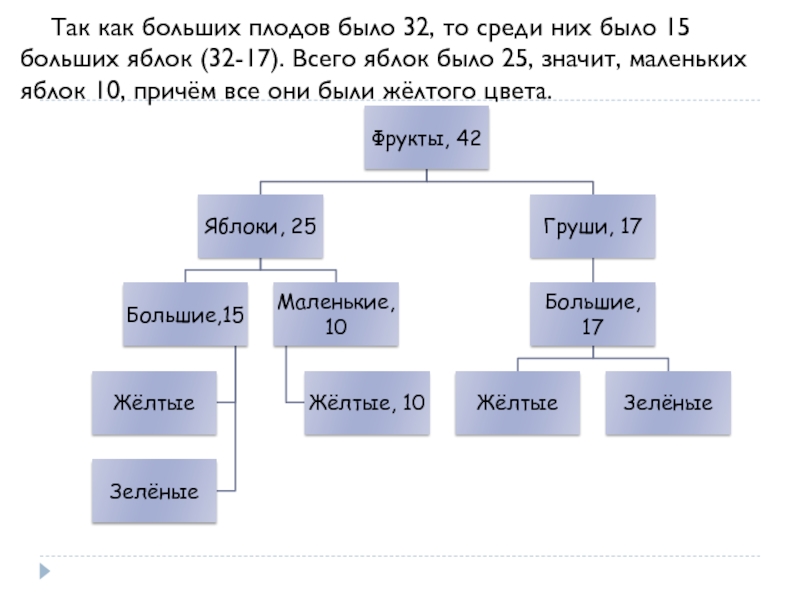
- 26. Так как больших плодов было 32, то
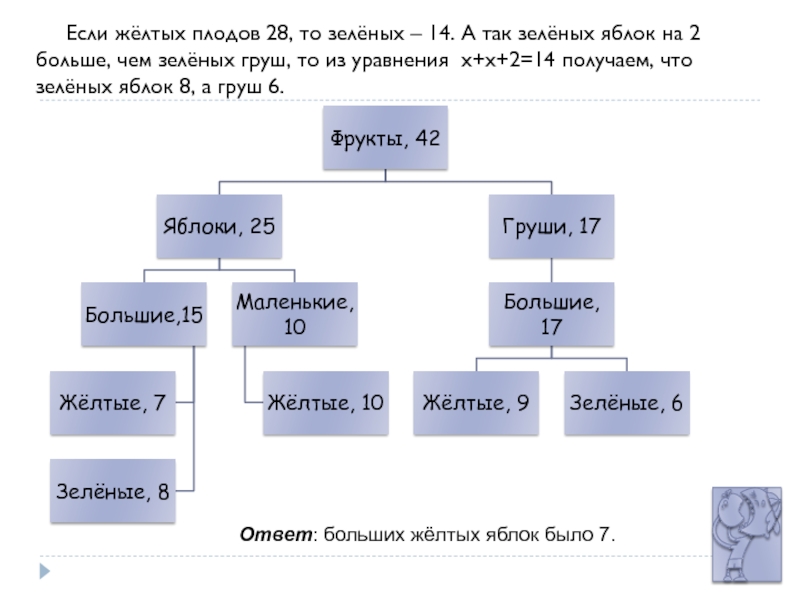
- 27. Если жёлтых плодов 28, то зелёных –
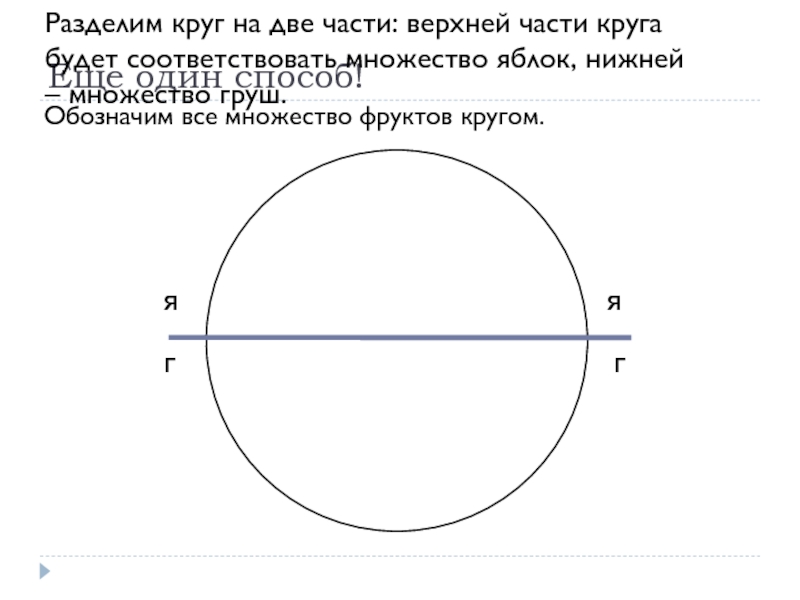
- 28. Еще один способ!Обозначим все множество фруктов кругом.Разделим
- 29. Вертикальная линия разделит круг на две части, соответствующие большим и маленьким фруктам.ЯЯГГ
- 30. Цвет фруктов учтем, изобразив круг меньшего радиуса:
- 31. Отметим на этой схеме исходные данные:ЯЯГГНет маленьких
- 32. Решение задач с помощью кругов Эйлера. Любители спорта
- 33. В классе 35 учеников, каждый из которых
- 34. Пусть круг Ф, состоящий из
- 35. Всего в классе 35 учеников,
- 36. Рассуждая аналогично найдем:35 - (24
- 37. Значит, 35 - (3 + 7 +
- 38. Надо выяснить, сколько школьников в группе VII.(V
- 39. Алгоритмическая линияРазвитие мышления Развитие мировоззрения учащихсяФормирование умений
- 40. Методические приёмыв беседе с учениками подробно обсуждается
- 41. Задачи о переправахДва солдата подошли к реке,
- 42. Цепочка задачТуристы (отец, мать и два брата-близнеца)
- 43. Цепочка задачНа реке во время половодья оторвало
- 44. От Кузнечика до …
- 45. От Кузнечика до …3 – 2 способа
Слайд 2Табличный способ
решения логических задач
Объекты двух классов могут находиться в отношении
в этих классах одинаковое количество объектов;
каждый объект первого класса связан заданным свойством только с одним объектом второго класса.
В соответствующей таблице типа ООО (объекты-объекты-один) в каждой строке и каждой графе будет находиться только одна 1 (один +), фиксирующая наличие связи между объектами.
Слайд 3Однажды в Артеке за круглым столом оказалось пятеро ребят родом из
Москвич сидел между томичем и Витей, санкт-петербуржец – между Юрой и Толей, а напротив него сидел пермяк и Алёша. Коля никогда не был в Санкт-Петербурге, а Юра не бывал в Москве и Томске, а томич с Толей регулярно переписываются.
Определите, в каком городе живёт каждый из ребят.
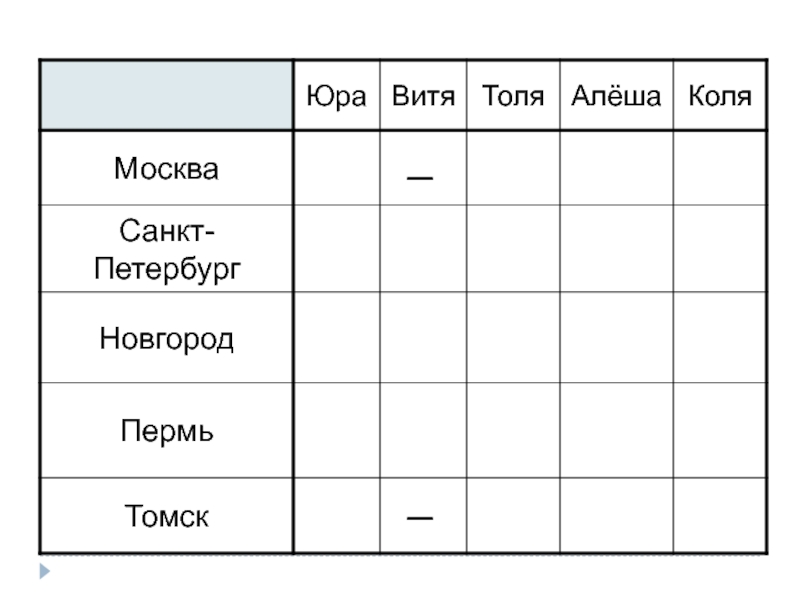
Слайд 5Однажды в Артеке за круглым столом оказалось пятеро ребят родом из
Москвич сидел между томичем и Витей, санкт-петербуржец – между Юрой и Толей, а напротив него сидел пермяк и Алёша. Коля никогда не был в Санкт-Петербурге, а Юра не бывал в Москве и Томске, а томич с Толей регулярно переписываются.
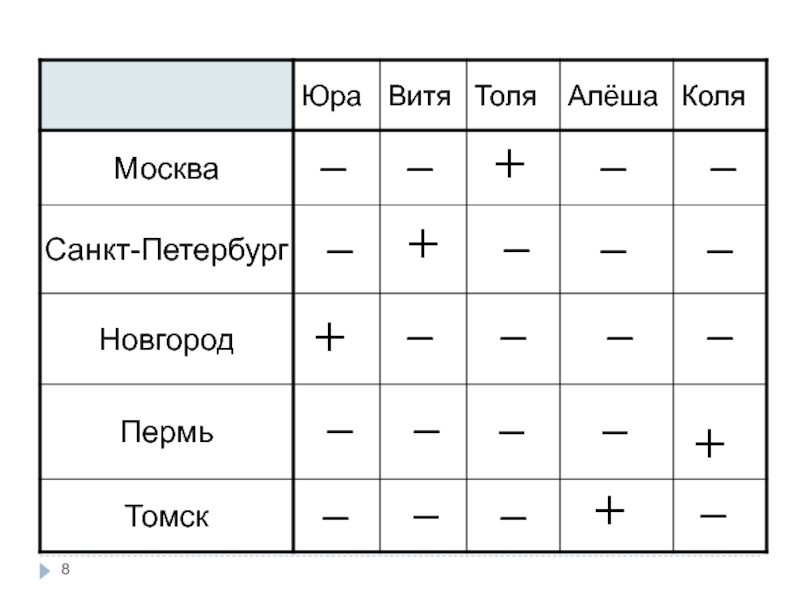
Слайд 7Однажды в Артеке за круглым столом оказалось пятеро ребят родом из
Москвич сидел между томичем и Витей, санкт-петербуржец – между Юрой и Толей, а напротив него сидел пермяк и Алёша. Коля никогда не был в Санкт-Петербурге, а Юра не бывал в Москве и Томске, а томич с Толей регулярно переписываются.
Слайд 9Ответ: Юра живёт в Новгороде,
Толя живёт в Москве,
Алёша живёт в Томске,
Коля живёт в Перми.
Слайд 10Три подружки
Три подружки, Аня, Света и Настя, купили различные молочные коктейли
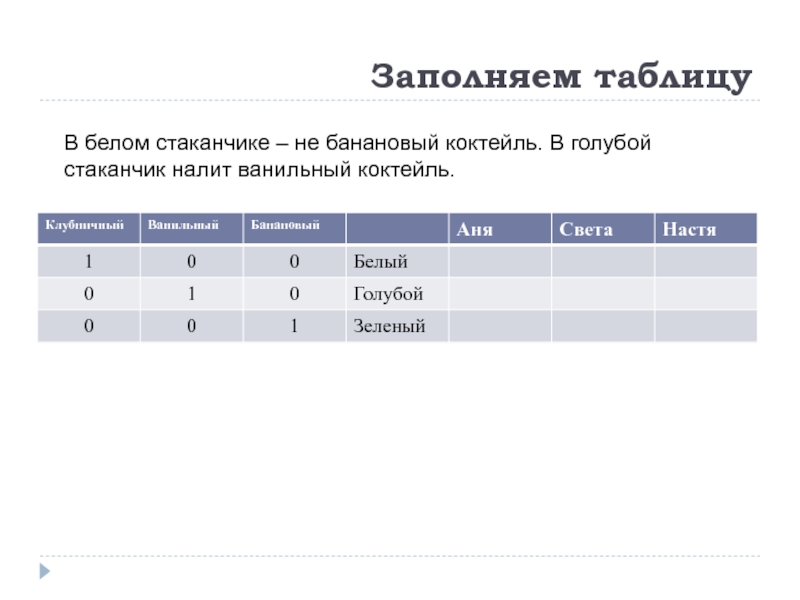
Ане достался не белый стаканчик, а Свете – не голубой. В белом стаканчике – не банановый коктейль. В голубой стаканчик налит ванильный коктейль. Света не любит клубничный коктейль.
Какой коктейль купила Настя и в каком стаканчике?
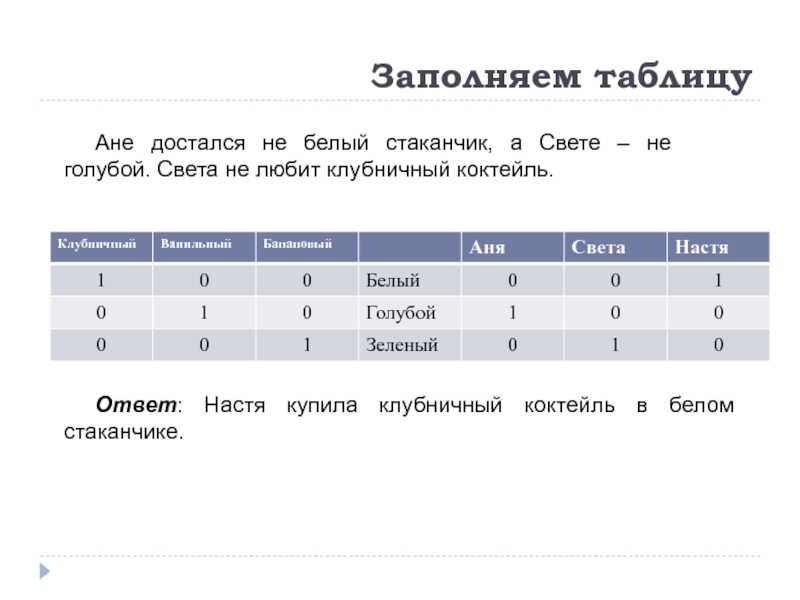
Слайд 11Заполняем таблицу
В белом стаканчике – не банановый коктейль. В голубой стаканчик
Слайд 12Заполняем таблицу
Ане достался не белый стаканчик, а Свете – не голубой.
Ответ: Настя купила клубничный коктейль в белом стаканчике.
Слайд 13Решение задач с помощью графов
Любитель скейтборда.
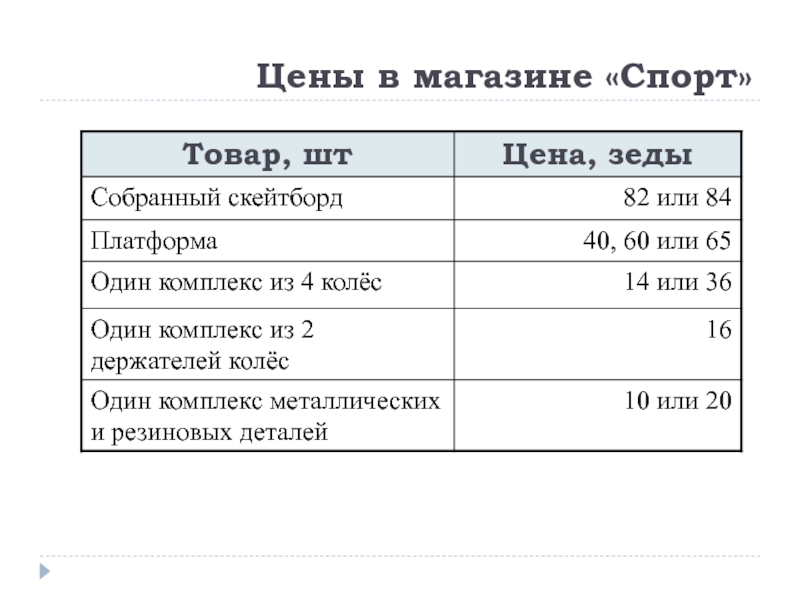
Сергей - большой любитель скейтборда. Он
В этом магазине можно купить полностью собранный скейтборд. Но можно купить:
платформу,
один комплект из 4 колёс,
один комплект из 2 держателей колёс,
комплект металлических и резиновых
деталей (подшипники, резиновые
прокладки, болты и гайки),
и собрать свой собственный скейтборд.
Слайд 15Вопросы
Сколько различных скейтбордов может собрать Сергей из предлагаемых составных частей?
Сколько
Сколько будет стоить самый дорогой скейтборд?
У Сергея 120 зедов, и он хочет собрать самый дорогой скейтборд, который может себе позволить за эти деньги. Какова стоимость и состав этого скейтборда?
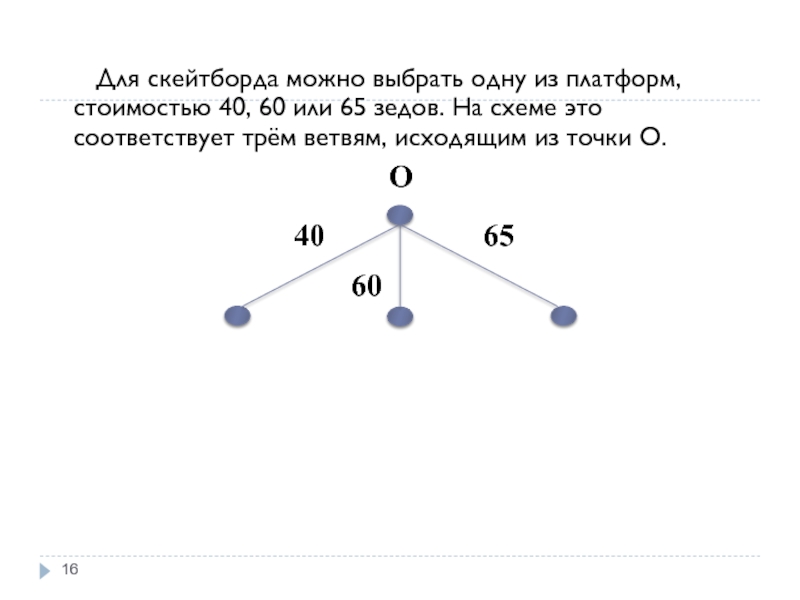
Слайд 16 Для скейтборда можно выбрать одну из платформ, стоимостью 40,
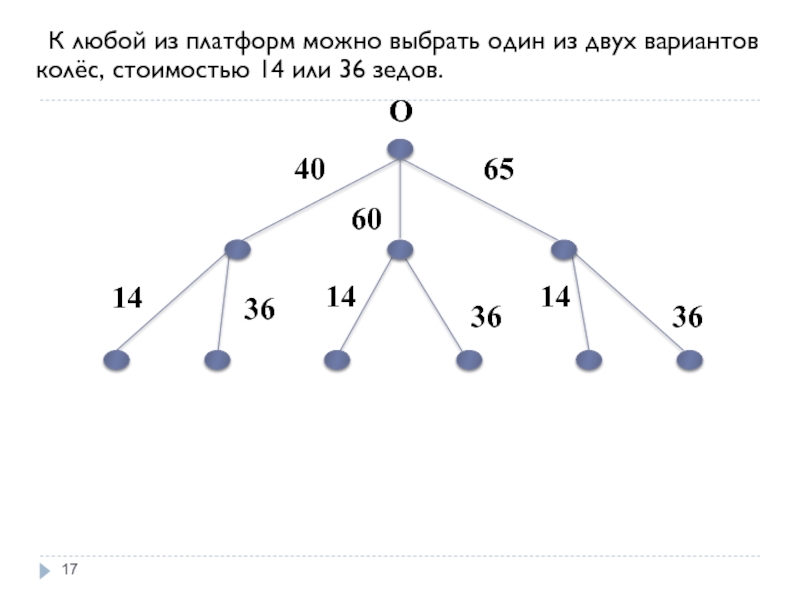
Слайд 17 К любой из платформ можно выбрать один из двух вариантов
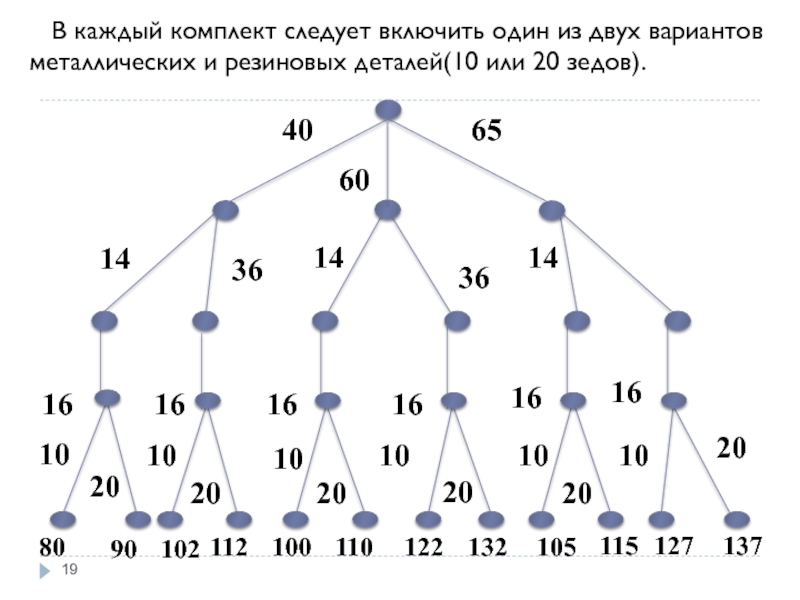
Слайд 19 В каждый комплект следует включить один из двух вариантов
Слайд 20Анализ полученных результатов
Всего можно собрать 12 различных скейтбордов. Самый дешевый из
Самый дорогой скейтборд, который может позволить себе Сергей, будет стоить 115 зедов и состоять из платформы за 65 зедов, колёс за 14 зедов, держателей для колёс за 16 зедов, комплекта металлических и резиновых деталей за 20 зедов.
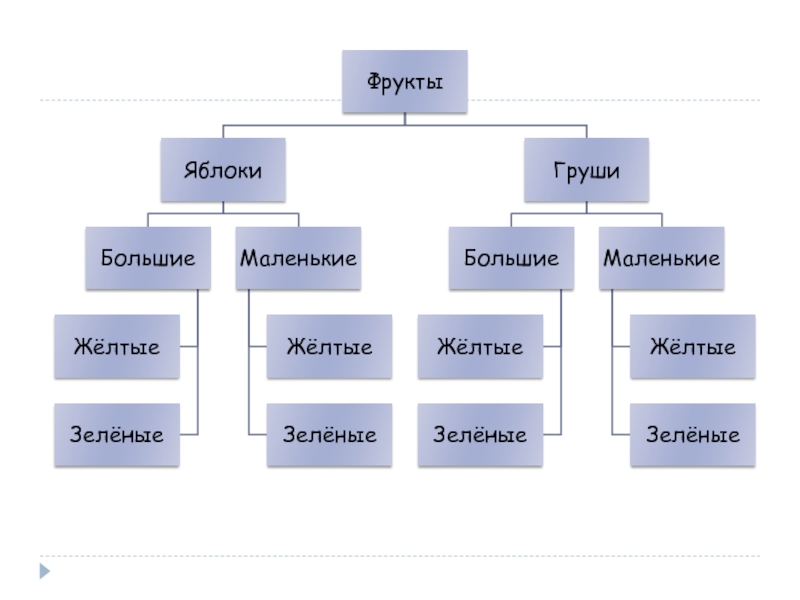
Слайд 22Бабушка прислала Ивану посылку с яблоками и грушами. Некоторые из этих
Сколько было таких яблок?
Слайд 25 Так как маленьких груш не было, то все они
Слайд 26Так как больших плодов было 32, то среди них было 15
Слайд 27Если жёлтых плодов 28, то зелёных – 14. А так зелёных
Ответ: больших жёлтых яблок было 7.
Слайд 28Еще один способ!
Обозначим все множество фруктов кругом.
Разделим круг на две части:
Я
Я
Г
Г
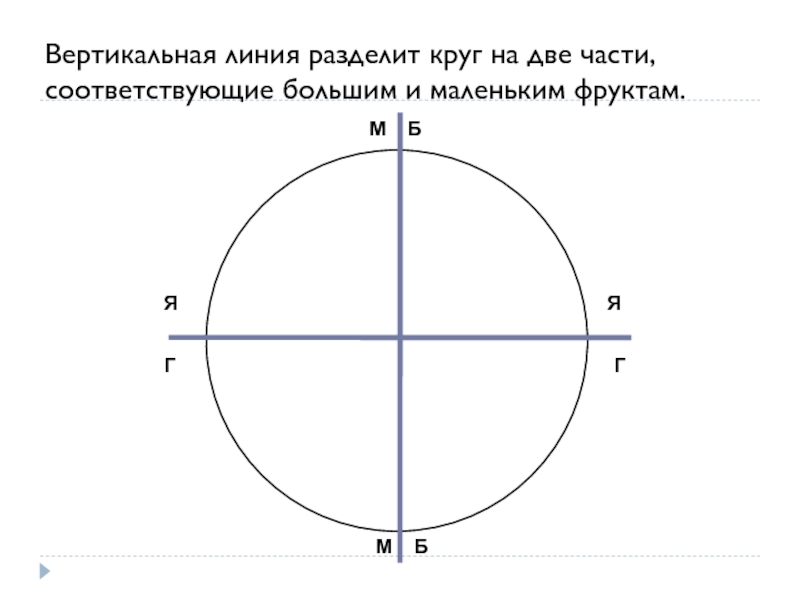
Слайд 29Вертикальная линия разделит круг на две части, соответствующие большим и маленьким
Я
Я
Г
Г
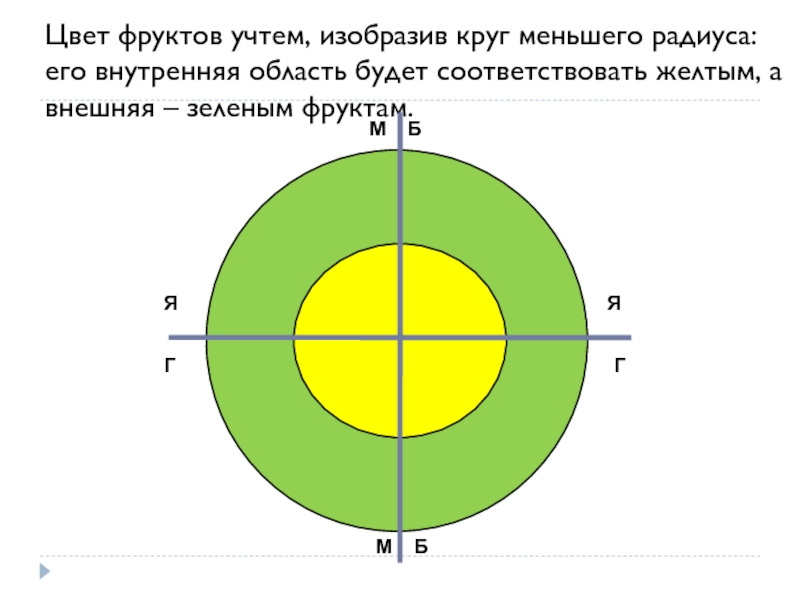
Слайд 30Цвет фруктов учтем, изобразив круг меньшего радиуса: его внутренняя область будет
Я
Я
Г
Г
Слайд 31Отметим на этой схеме исходные данные:
Я
Я
Г
Г
Нет маленьких груш.
Нет маленьких зеленых яблок.
Всего
32 больших и 10 маленьких.
10
Желтых плодов 28, зеленых – 14. Так как зеленых яблок на 2 больше, чем зеленых груш, то их 8, а груш – 6.
8
6
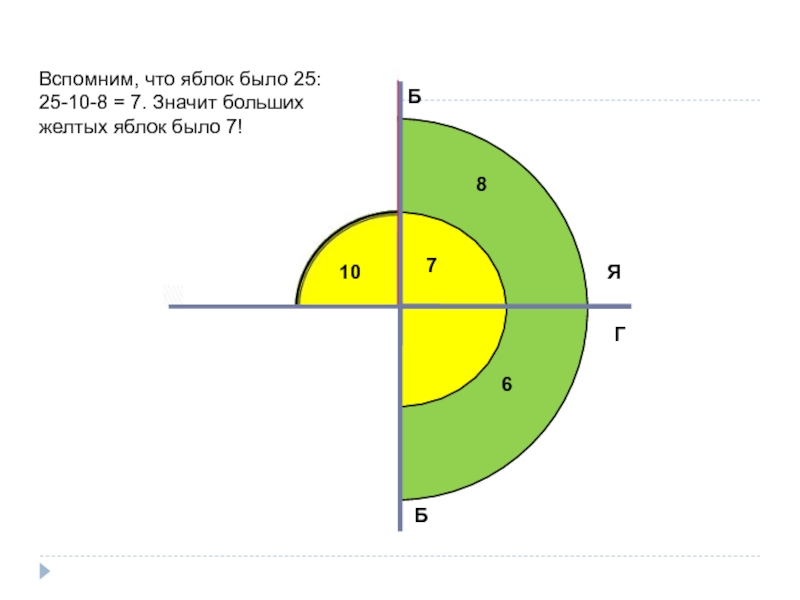
Вспомним, что яблок было 25:
25-10-8 = 7. Значит больших желтых яблок было 7!
7
Слайд 33В классе 35 учеников, каждый из которых любит футбол, волейбол или
24 из них любят футбол, 18 – волейбол, 12 – баскетбол.
Кроме того, 10 учеников одновременно любят и футбол и волейбол, 8 – футбол и баскетбол, а 5 – волейбол и баскетбол.
Сколько учеников этого класса любят все три вида спорта?
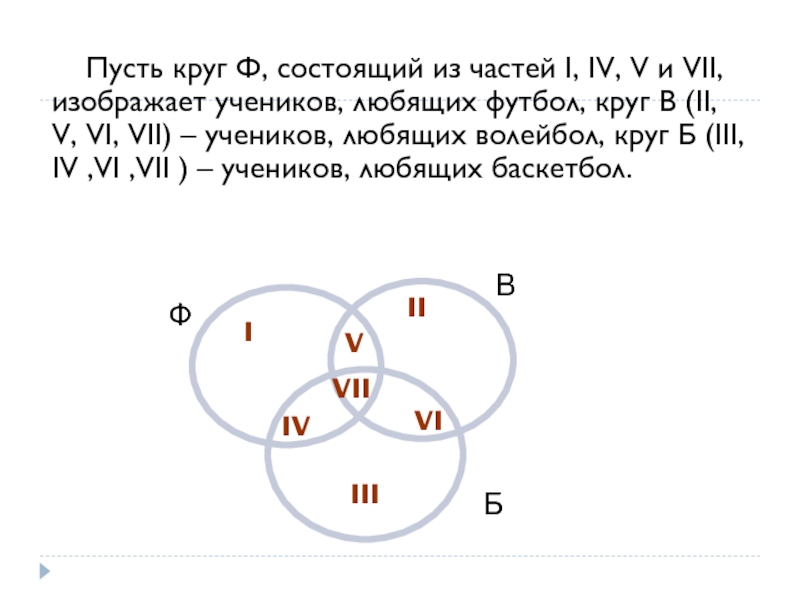
Слайд 34 Пусть круг Ф, состоящий из частей I, IV, V
Ф
Б
В
I
II
V
VII
IV
VI
III
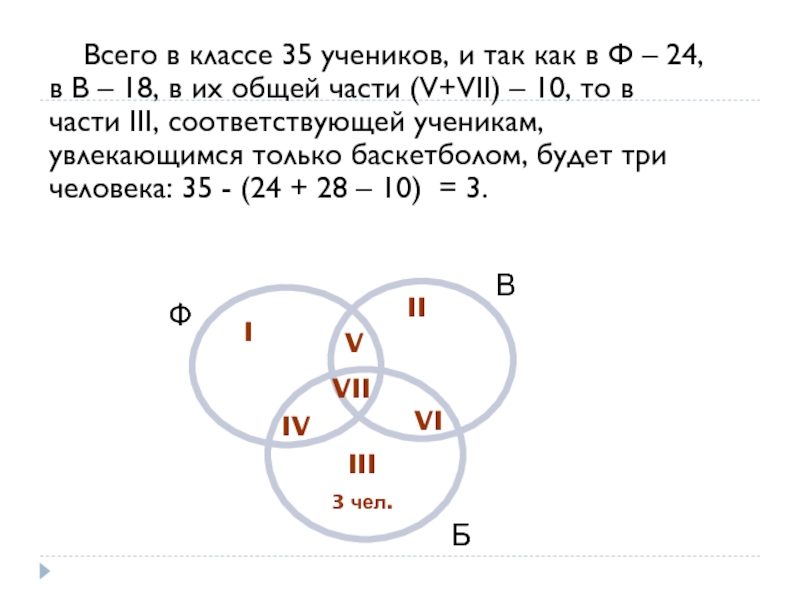
Слайд 35 Всего в классе 35 учеников, и так как в
Ф
В
I
II
V
VII
IV
VI
III
3 чел.
Б
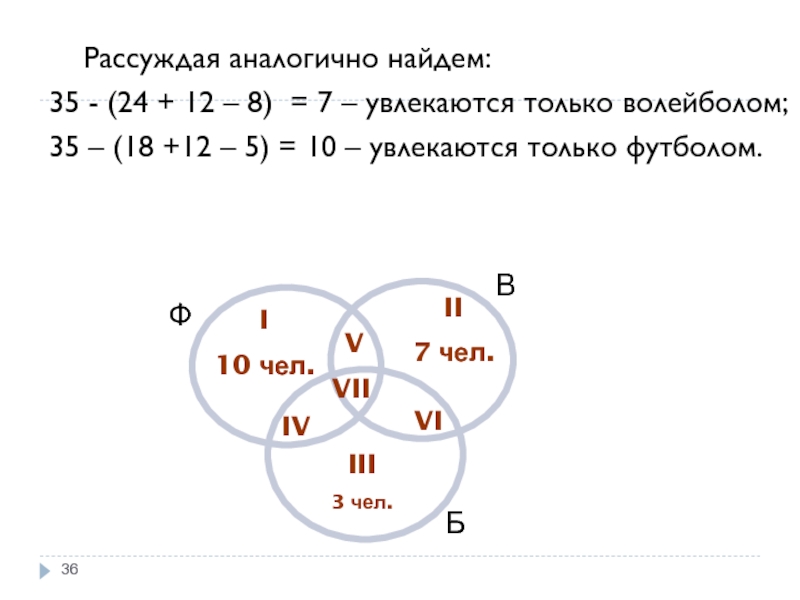
Слайд 36 Рассуждая аналогично найдем:
35 - (24 + 12 – 8)
35 – (18 +12 – 5) = 10 – увлекаются только футболом.
Ф
В
I
10 чел.
II
7 чел.
V
VII
IV
VI
III
3 чел.
Б
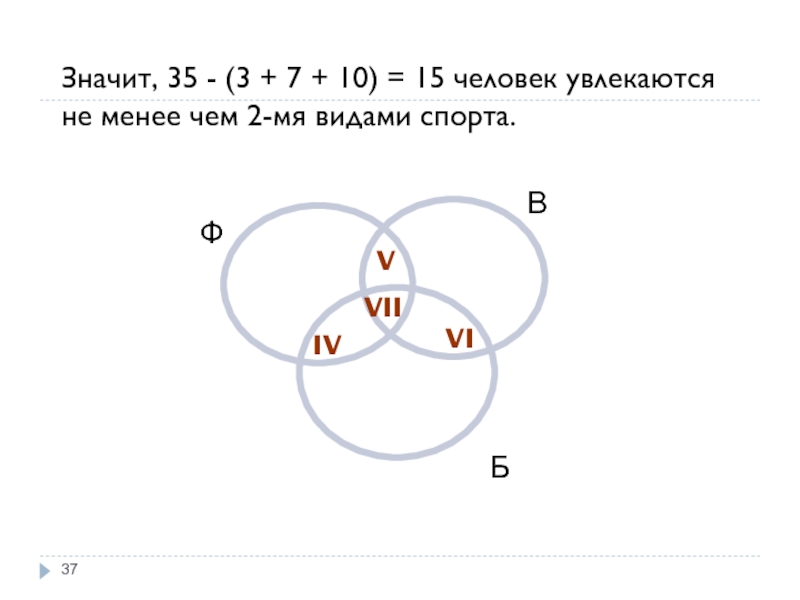
Слайд 37Значит, 35 - (3 + 7 + 10) = 15 человек
Б
Ф
В
V
VII
IV
VI
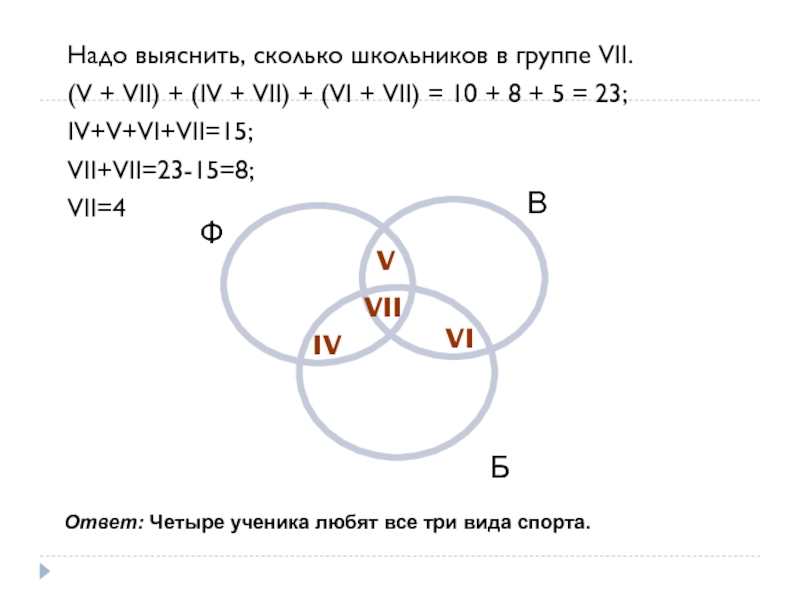
Слайд 38Надо выяснить, сколько школьников в группе VII.
(V + VII) + (IV
IV+V+VI+VII=15;
VII+VII=23-15=8;
VII=4
Б
Ф
В
V
VII
IV
VI
Ответ: Четыре ученика любят все три вида спорта.
Слайд 39Алгоритмическая линия
Развитие мышления
Развитие мировоззрения учащихся
Формирование умений и навыков, полезных в
задачи о переправах
задачи о разъездах
задачи о переливаниях
задачи о взвешиваниях
Слайд 40Методические приёмы
в беседе с учениками подробно обсуждается решение ключевой задачи;
ученикам
на заключительном этапе ученикам предлагается задача, решение которой предполагает применение полученных знаний и умений в новой ситуации;
в зависимости от уровня подготовленности учеников им могут быть предложены задачи разного уровня сложности;
для решения алгоритмических задач широко используются виртуальные лаборатории «Переправы», «Разъезды», «Переливания» и «Взвешивания»;
широко применяются разнообразные формы записи решений алгоритмических задач: описание на естественном языке; списки; таблицы; схемы; презентации; файлы с решением, полученным в виртуальной лаборатории.
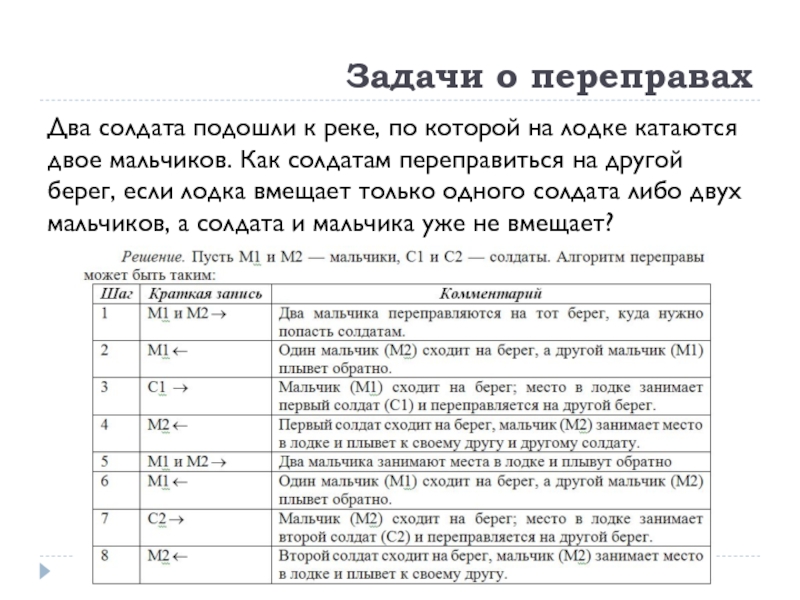
Слайд 41Задачи о переправах
Два солдата подошли к реке, по которой на лодке
Слайд 42Цепочка задач
Туристы (отец, мать и два брата-близнеца) должны переправиться через реку.
Слайд 43Цепочка задач
На реке во время половодья оторвало от берега и унесло
У причала стояла лодка, которая могла перевозить не больше двух человек. К реке подошли четверо, которым было необходимо переправиться на противоположный берег. Все они переправились через реку без посторонней помощи и продолжили свой путь, причем лодку поставили на тот же причал, откуда её и взяли. Возможно ли это?
Слайд 45От Кузнечика до …
3 – 2 способа (программы)
5, 7 – 2
9 можно получить из 3 (2 сп.) + из 7 (2 сп.) – 4 способа
11, 13 – 4 способа
15, 14, 19 – 6 способов
21, 23, 25 – 8 способов